Частные решения волнового уравнения.

1. Плоские и комплексные волны.

Рассмотрим частный случай общего решения, считая коэффициенты действительными

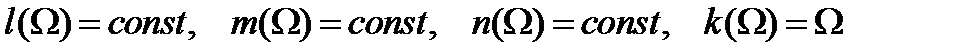. (7)

Тогда (5) примет форму 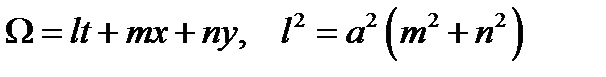. Данное решение 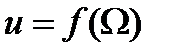можно переписать в форме 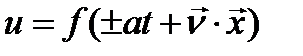, где уравнение 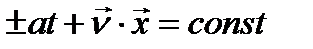представляет собой уравнение плоскости, которая во времени перемещается по нормали 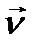со скоростью 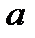. Знаки соответствуют направлению распространения данного плоского фронта. Данное решение соответствует плоским волнам.

Другой частный случай 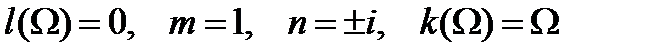мы получим общие интегралы уравнения Лапласа

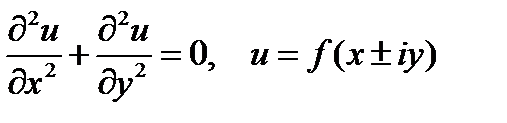. (8)

В том случае, когда все три коэффициента отличны от нуля и являются комплексными величинами с различными аргументами, мы получаем уже существенно новое решение, которое В.И. Смирнов и С.Л. Соболев назвали плоской комплексной волной (с физической точки зрения это решение не является плоской волной в привычном смысле этого понятия).

Если коэффициент , то его не нарушая общности можно положить равным единице, поскольку

.

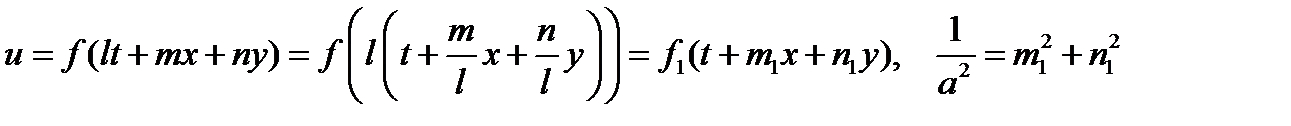Опуская индексы и вводя обозначения 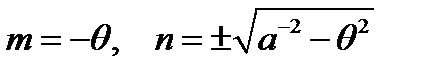, получим решение вида

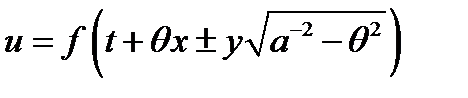. (9)

Так как (9) удовлетворяет волновому уравнению, то и действительная и мнимая часть (9)

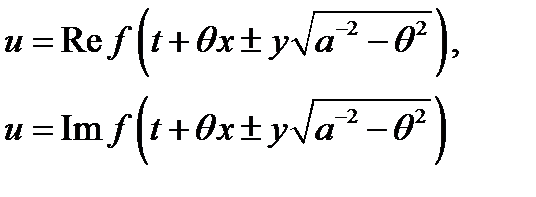(10)

также являются решениями волнового уравнения.

Рассмотрим несколько примеров приложения данного решения к конкретным задачам теории упругости.