Отражение плоских волн от границы упругой полуплоскости со свободной поверхностью.

Воспользуемся представлением Ламе для решений динамических уравнений теории упругости

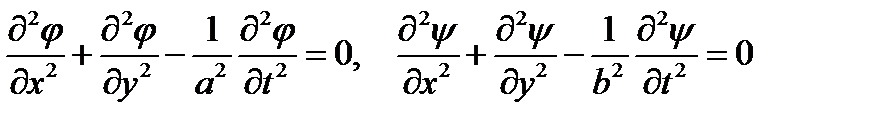. (11)

Назовём плоской продольной волной (11) (PV – волной) решение вида

,

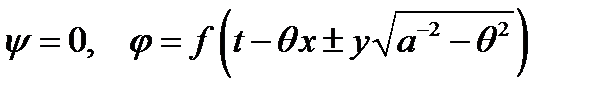где коэффициенты 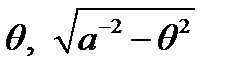являются действительными. Если рассматриваются колебания упругой полуплоскости, вызванные продольной волной, то волной идущей к границе назовём решение вида

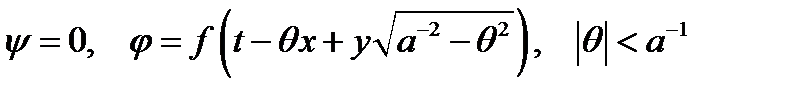. (12)

Отражённой плоской продольной волной будем считать решение

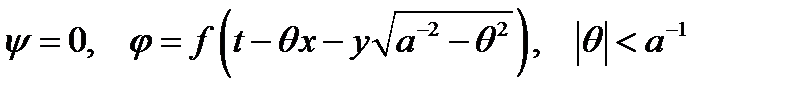. (13)

Аналогичные обозначения можно ввести для поперечных волн (падающей и отражённой):

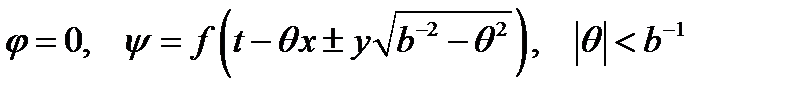. (14)

Мы рассматриваем здесь поперечные волны с вектором поляризации, лежащим в плоскости 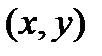.В мировой литературе такие волны часто называютSV волнами, в отличие от поперечных волн, для которых вектор поляризации перпендикулярен плоскости 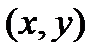. Такие волны, соответствующие антиплоской деформации, называютHV волнами.

Геометрический смысл названия волн, падающих и отраженных, состоит в том, что в волнах, идущих к границе полуплоскости, потенциал сохраняет свое постоянное значение на плоскостях

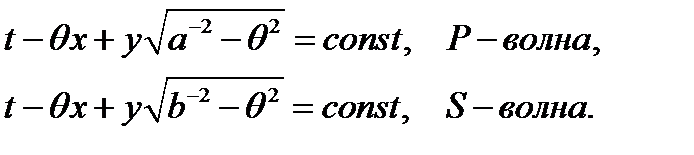
Эти плоскости перемещаются при возрастании времени так, что направление их движения 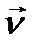, характеризуемое направляющими косинусами, которые составляют тупой угол с осью :

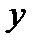(15)

В отражённых волнах этот угол будет острым:

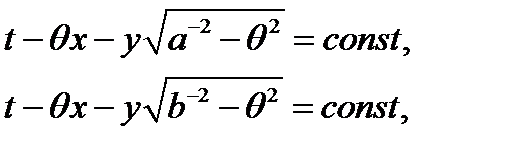
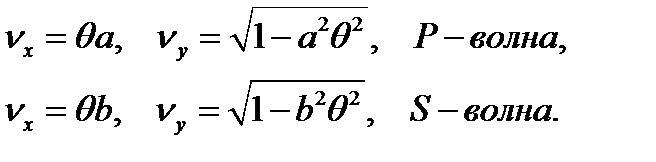(16)

При падении волны на свободную поверхность на границе полуплоскости должны быть выполнены следующие граничные условия:

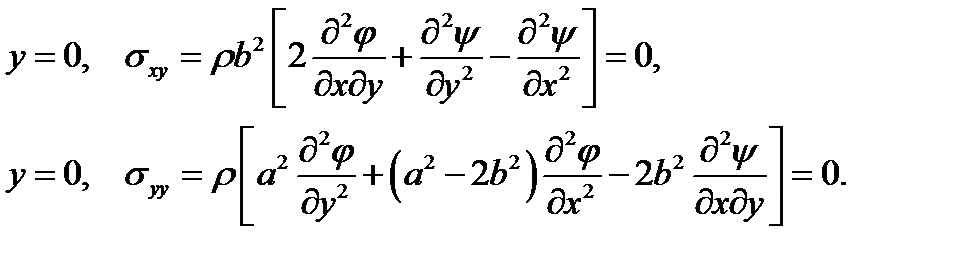(17)

Рассмотрим случай падения продольной волны, описываемой потенциалами (12), которые мы снабдим индексом 1:

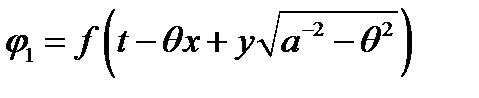. (18)

Отраженные продольную и поперечную волну будем отличать индексом 2:

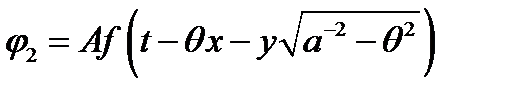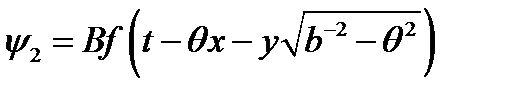, . (19)