Волны в упругой пластине.

Рассмотрим волны в слое упругой среды 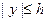, считая отличными от нуля перемещения:

.

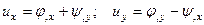Потенциалы продольных и поперечных волн должны удовлетворять волновым уравнениям

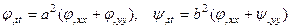(1)

и граничным условиям на поверхностях пластины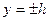

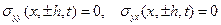. (2)

Если искать решение в виде бегущих вдоль слоя волн

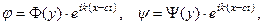(3)

получим из (1) для функций 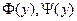уравнения:

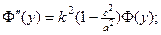
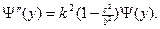
Решениями данных уравнений являются функции

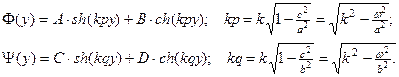(4)

Компоненты вектора напряжений равны:

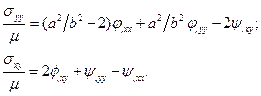(5)

Подстановка решений в граничные условия (2) приводит к однородной системе четырех уравнений. Приравнивая определитель к нулю мы, как и в случае волн Рэлея и Лява, получим уравнение, связывающее скорость волны с ее частотными характеристиками. Поскольку задача получится достаточно громоздкой, исследуем отдельно решения двух типов. Сначала рассмотрим решение вида

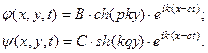(6)

Перемещения для данного решения равны

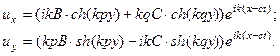(7)

Подстановка (6) в (5) дает компоненты вектора напряжений:

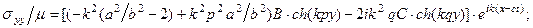(8)

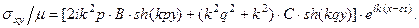(9)

Как показывают полученные выражения (7), (8), (9), рассматриваемое решение соответствует модам колебаний, симметричным относительно плоскости 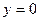(рис.1(а)).

Учитывая симметрию, можно выполнить граничные условия только на одной границе :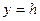

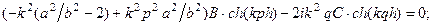
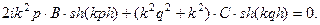
Приравнивая определитель данной системы к нулю, получим дисперсионное характеристическое уравнение:

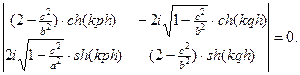
Уравнение приводится к виду

.

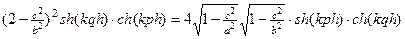После деления на гиперболические косинусы, получим:

.

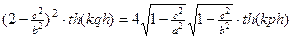При значениях 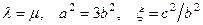получим для больших величин 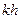, когда гиперболический тангенс близок к единице, уравнение Рэлея

.

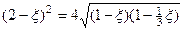При малых значениях величины 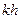тангенсы можно заменить их аргументами

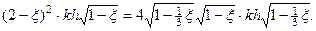
Производя упрощения, получим

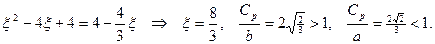
Таким образом, можно заключить, что первая мода симметричных колебаний распространяется для коротких волн со скоростью, близкой к скорости волн Рэлея, а для волн с очень большой длиной волны со скоростью 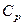, которая больше чем скорость поперечных волн и меньше, чем скорость продольных волн. Можно показать, что зависимость скорости от величины 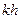носит монотонный характер. Скорость асимптотически уменьшается от величины 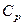до величины 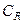с увеличением .

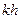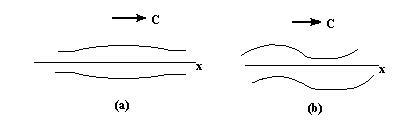
Рис.1 Симметричные (а) и антисимметричные (b) колебания пластины

Решение другого вида

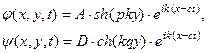
описывает несимметричные колебания пластины, поскольку перемещения при таком решении имеют следующий вид:

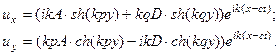
Видно, что поперечные смещения одинаковы по разные стороны от плоскости 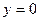, а продольные антисимметричны (рис.1(b)). Граничные условия в этом случае дают:

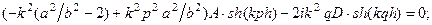
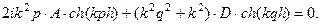
Приравнивая определитель к нулю, получим:

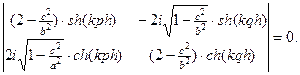
Полученное уравнение

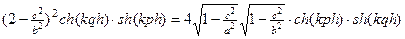
приводится к виду

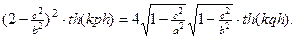
При больших значениях 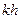(короткие волны) получим уравнение Рэлея. При малых значениях 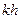(длинные волны) получим уравнение:

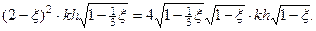
Решая уравнение, находим:

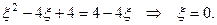
Таким образом, длинные волны распространяются по пластине со скоростью близкой к нулю. С уменьшением длины волны скорость возрастает, асимптотически приближаясь к скорости волн Рэлея.