Волны в стержнях с круглым сечением.

Рассмотрим волны, бегущие по стержню круглого сечения, имеющию ось симметрии (рис.2).

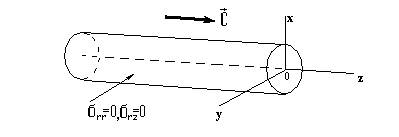
Рис.2 Волны бегут вдоль оси цилиндра радиуса r=a со скоростью С. На боковой поверхности, свободной от усилий, должны быть выполнены граничные условия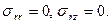

Это означает, что решение не зависит от полярного угла. В этом случае в цилиндрической системе координат 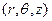отличными от нуля компонентами вектора перемещений будут 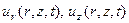. Отличные от нуля деформации

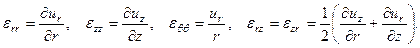
Соответственно отличными от нуля напряжениями будут:

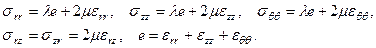
Получим уравнения движения в случае цилиндрической симметрии (Рис.1). Рассмотрим движение элементарного объема, приведенного на рис.1.

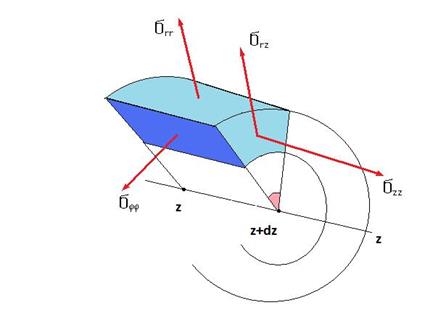
Рис.1.

В проекции на ось , получим

.

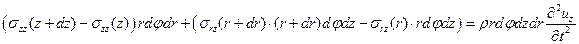Поделив на объем 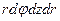и переходя к пределу, приходим к уравнению

.

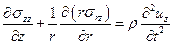Сделав аналогичную проекцию на ось 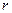, получим

.

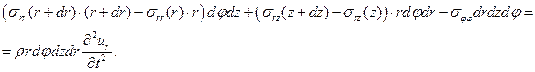После деления на объем и предельного перехода, получим

.

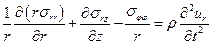После подстановки выражений для напряжений получим уравнения движения в перемещениях:

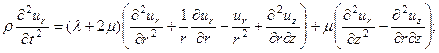
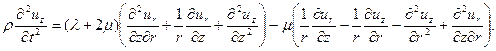
Будем искать их в форме

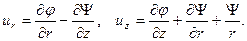(10)

Подстановка в уравнения движения приводит к следующим уравнениям для функций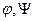

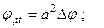(11)

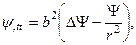
где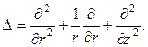

Если ввести новую искомую функцию

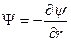, (12)

она будет удовлетворять волновому уравнению

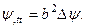(13)

При этом перемещения будут такими:

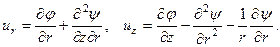(14)

Напряжения, участвующие в граничных условиях, получаются в форме следующих выражений:

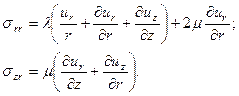(15)

Таким образом, задача сводится к решению волновых уравнений (11),(13) с граничными условиями на боковой поверхности цилиндра

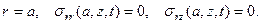(16)

Будем искать решение в виде волн, бегущих в направлении оси с неизвестной скоростью :

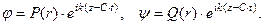(17)

Подстановка выражений (17) в волновые уравнения (11), (13) приводит к следующим уравнениям для неизвестных функций :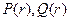

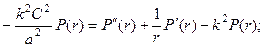(18)

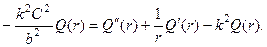
Поскольку уравнения функционально одинаковы, достаточно рассмотреть первое из них. Перепишем его в форме:

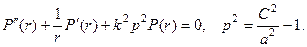
Замена 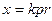приводит его к уравнению Бесселя

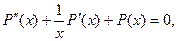
решениями которого будут функции Бесселя первого 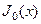и второго рода 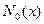. Первая из этих функций ограничена в точке 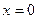, вторая не ограничена. Поскольку нам нужно решение, не имеющее особенности на оси цилиндра при 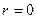, подходит функция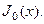

Функция Бесселя, как и остальные специальные функции, задается своим разложением в ряд

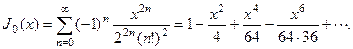(19)

Таким образом, решениями волновых уравнений будут выражения

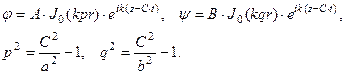(20)

Подставим полученные решения (20) в выражения для перемещений (14):

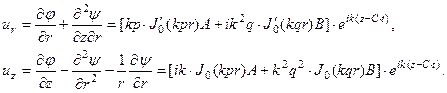(21)

Подставляя перемещения (21) в (15), находим деформации и напряжения, необходимые для подстановки в граничные условия:

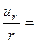
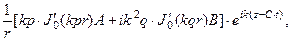
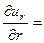
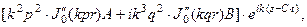
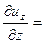
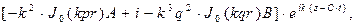
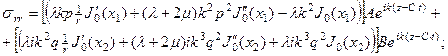
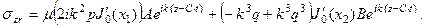
Приравнивая полученные напряжения к нулю в точке 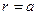, получим систему двух однородных уравнений:

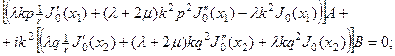
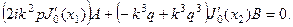
Равенство нулю определителя позволяет получить дисперсионное уравнение. Оно достаточно громоздко, поэтому ограничимся первым приближением, когда удерживаются слагаемые меньше второй степени от величины 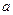. Учитывая разложение (19), получим

,

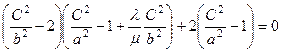решением которого будет значение

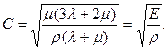(22)

Следующее приближение, найденное Л.Похгаммером, дает более точное значение

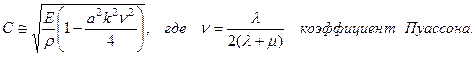(23)

Таким образом, скорость волн в стержне дается выражениями (22), (23). Обратим внимание на то, что уже второе приближение для скорости зависит от длины волны и радиуса стержня. Чем больше величина 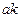, тем меньше скорость. Длинные волны распространяются более медленно, чем короткие. В результате волновой пакет размывается (Рис.2).

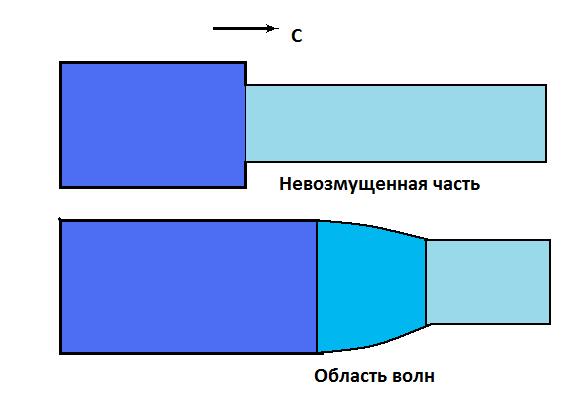
Рис.2

Этим мы завершаем экскурс по влиянию геометрии и граничных условий на скорость волн в упругих средах с границей.