Плоская задача Лэмба

Постановка задачи.Пусть в плоскости 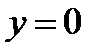, ограничивающей упругое полупространство 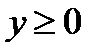, действует нагрузка 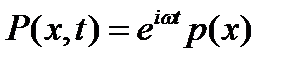. Требуется решить волновые уравнения для потенциалов продольных и поперечных волн

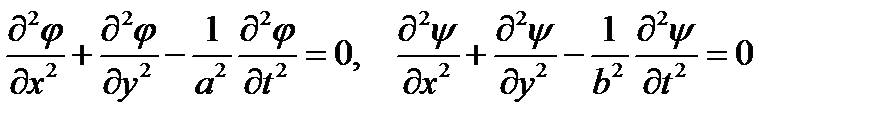. (1)

С граничными условиями на поверхности

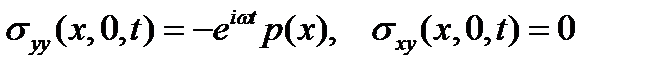. (2)

Перемещения и напряжения связаны с потенциалами следующими соотношениями:

;

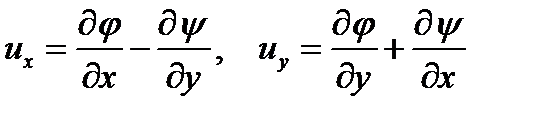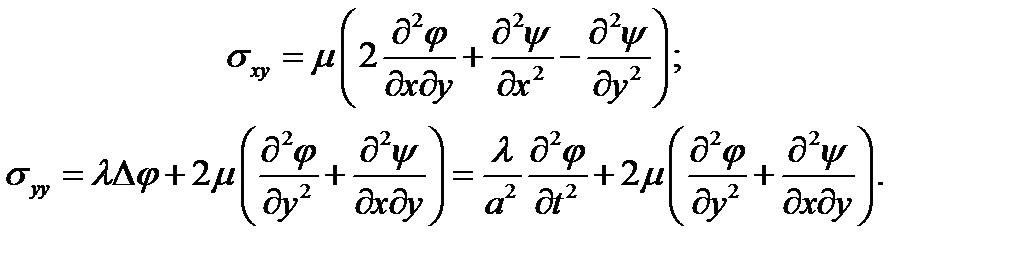(3)

Поскольку стационарные колебания можно выделить отдельным множителем, решение можно представить в форме:

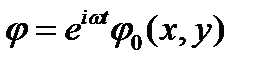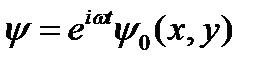, . (4)

Новые функции 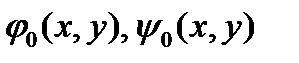будут удовлетворять уравнениям Гельмгольца

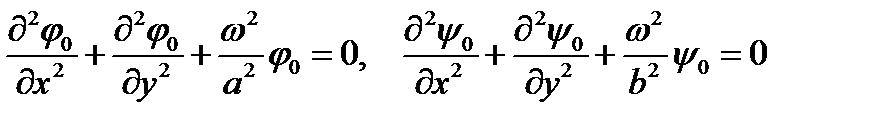. (5)

Будем решать уравнения (5) с помощью преобразования Фурье по переменной :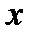

;

.

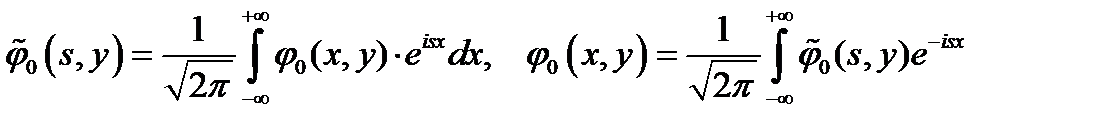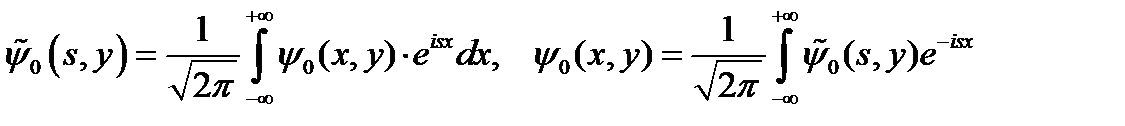После преобразования Фурье уравнений (5) для образов надо решить обыкновенные дифференциальные уравнения

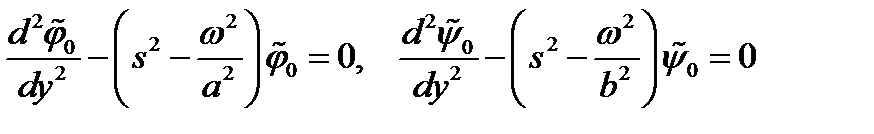. (6)

С учетом убывания решения на бесконечности, уравнения (6) имеют следующие решения:

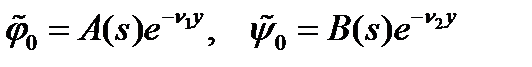, (7)

где .

Можно легко проверить, что уравнениям (1) удовлетворяют интегральные выражения

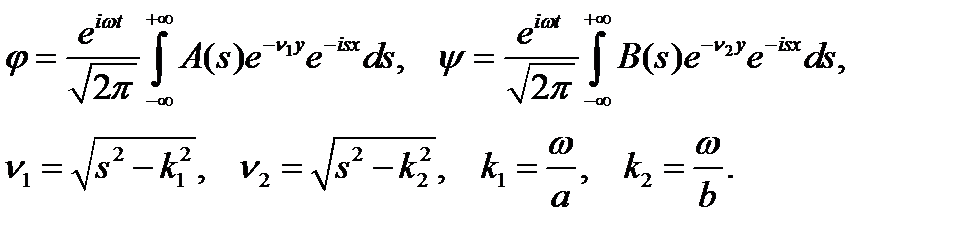(8)

Подставляя потенциалы (8) в выражения для перемещений и напряжений (3), получим:

.

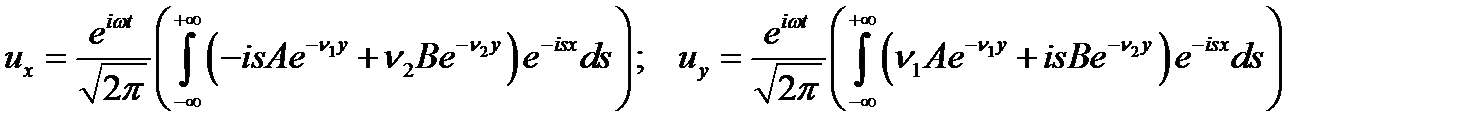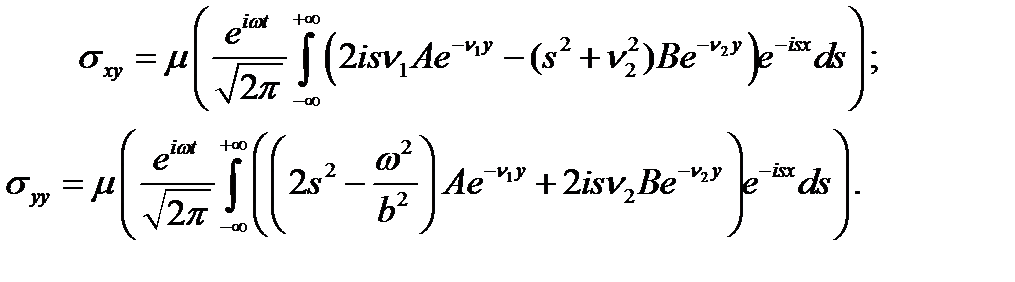(9)

Если применить к граничным условиям (2) преобразование Фурье и подставить образы напряжений, то это позволяет получить систему уравнений для определения неизвестных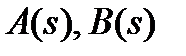

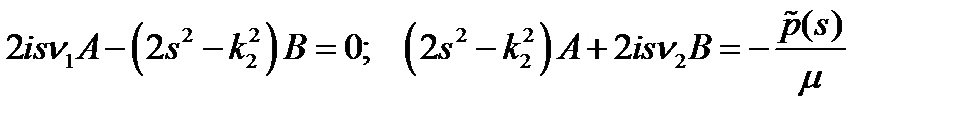, (10)

где .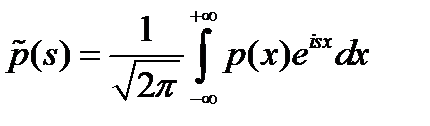

Решением системы уравнений (6) будет пара функций

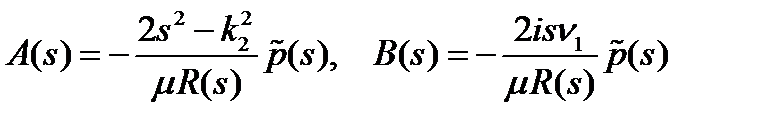, (11)

где .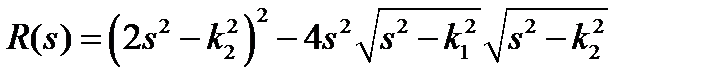

Подставляя в (9) полученные значения функций 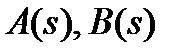из (11), найдем перемещения свободной поверхности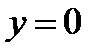

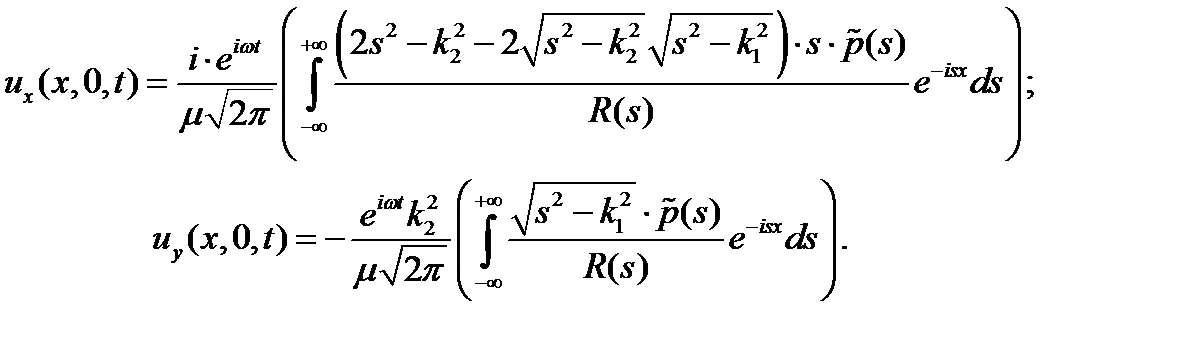(12)

Рассмотрим действие сосредоточенной силы 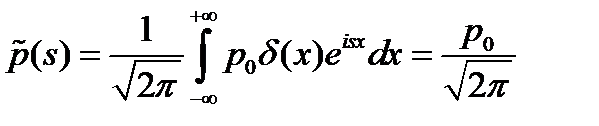. Подстановка в (12) приводит к выражениям:

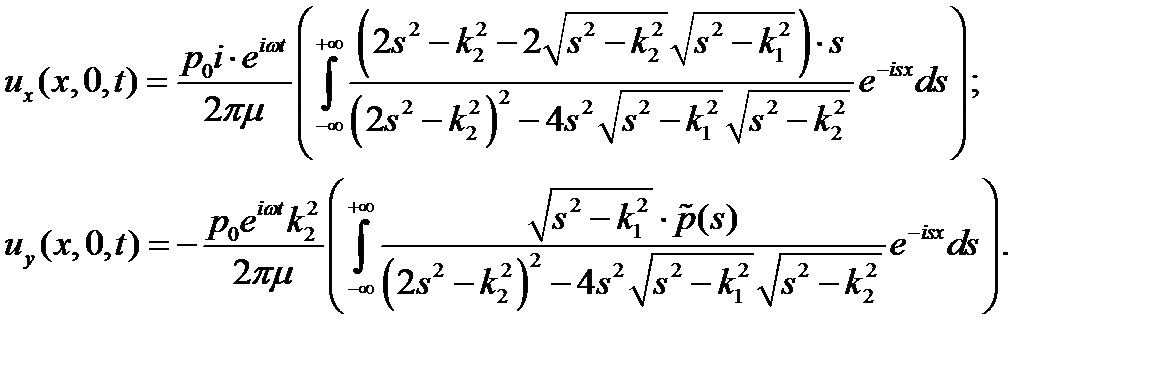(13)

В этом случае подстановка 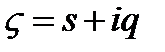позволяет свести определение перемещений к вычислению контурных интегралов

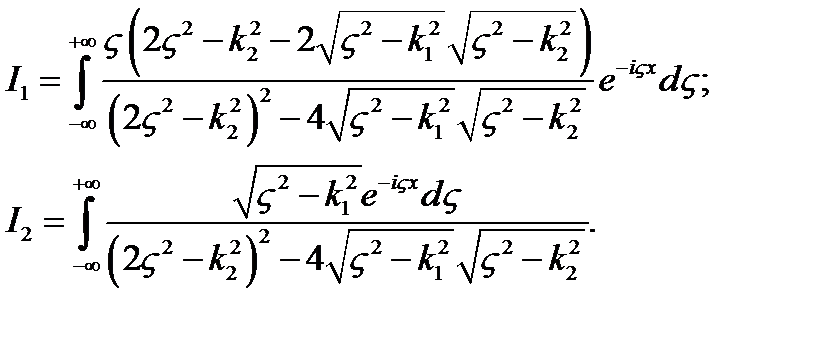(14)

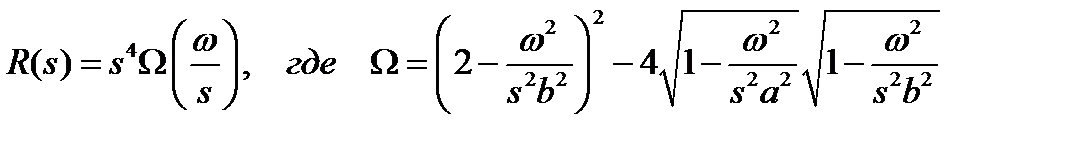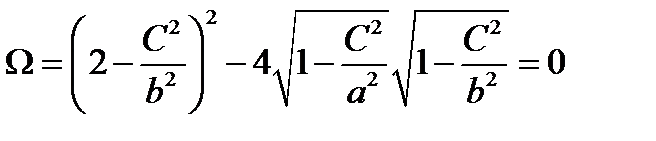Рассмотрим функцию Рэлея . Представим ее в виде . Обозначим . Если приравнять мы получим уравнение Рэлея с корнем, который равен 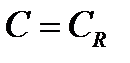.Это означает, что в окрестности точки 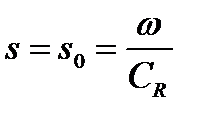. Знаменатель в (13) можно представить в виде 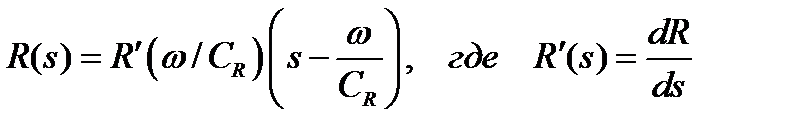. Это означает, что главный член разложения выражений, от которых берутся интегралы в (13), будет иметь вид:

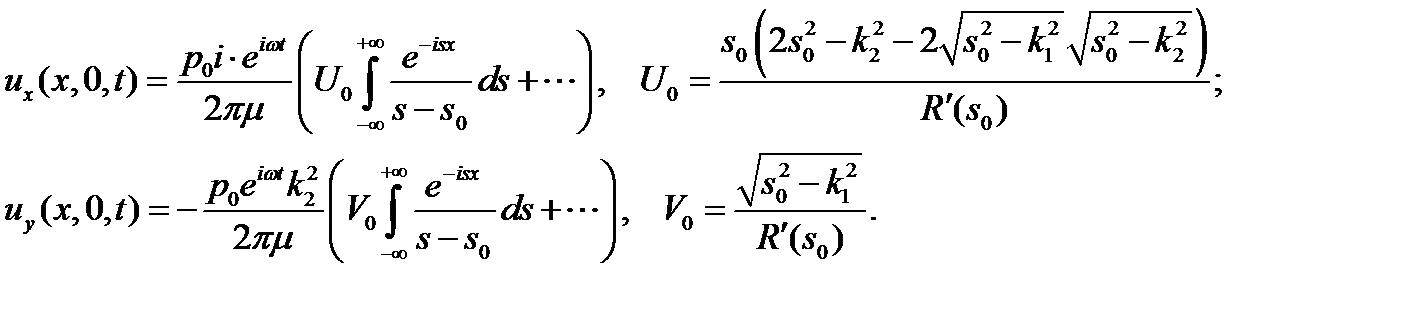
Интегралы от главной части вычисляются аналитически, поскольку сводятся к вычетам в полюсах. Это позволяет представить главные части выражений для перемещений в форме