Случай полного внутреннего отражения.

Решение для случая полного внутреннего отражения можно строить аналогично, но в этом случае придётся отказаться от требования 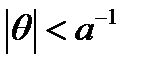. Рассмотрим два вспомогательных решения. В первом случае мы будем искать решение для верхней полуплоскости в виде

, ,

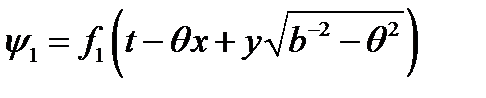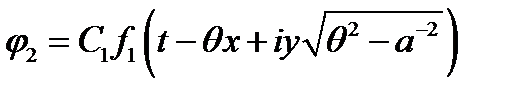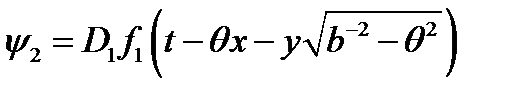. (23)

Во втором случае мы рассмотрим абсолютно аналогичную задачу для нижней полуплоскости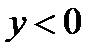

, ,

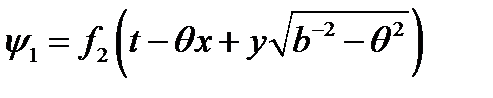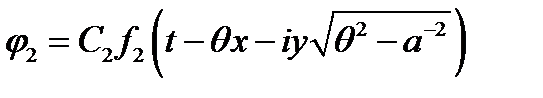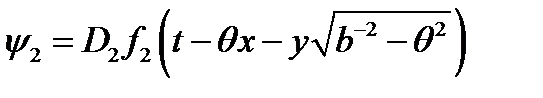. (24)

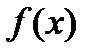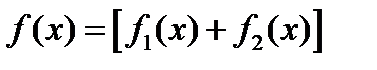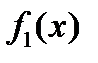С помощью данных решений можно построить отражение падающей поперечной волны в случае полного внутреннего отражения. Пусть рассматриваемую функцию можно представить в виде , где – краевое значение функции комплексной переменной, регулярной в верхней полуплоскости, а 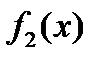– краевое значение функции комплексной переменной, регулярной в нижней полуплоскости. Такое представление возможно для достаточно широкого класса функций и дается интегралами типа Коши

, .

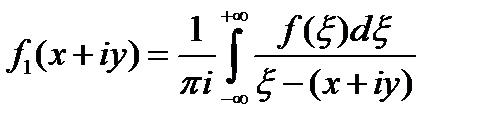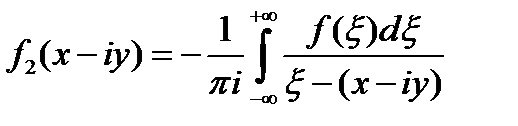В этом случае функции 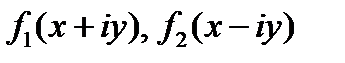являются комплексно сопряженными, причём 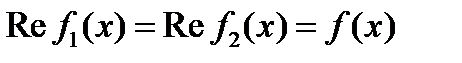. Тогда решение задачи полного внутреннего отражения можно представить в форме

,

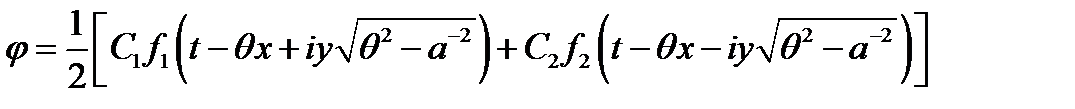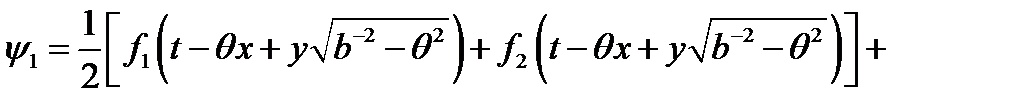(25)

.

;

;

.

.

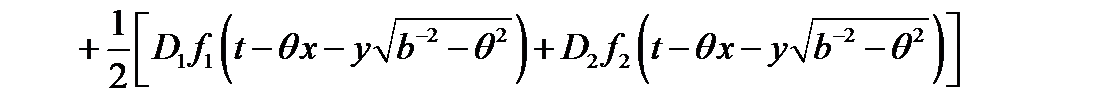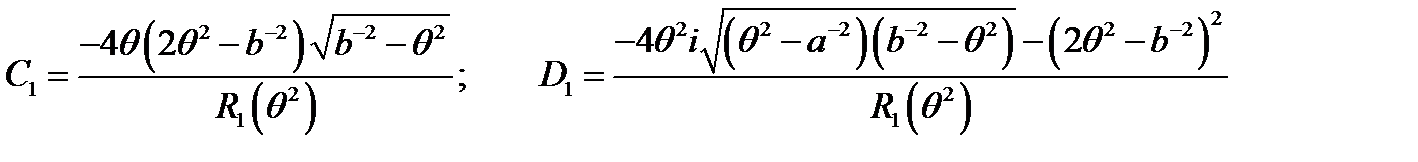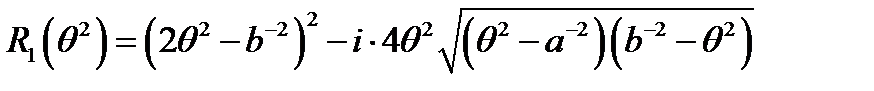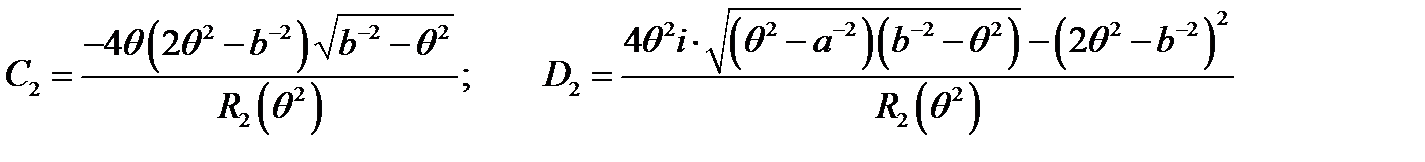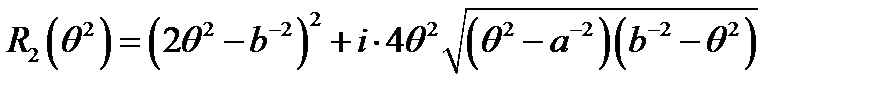Полученное решение является комплексным. Для выделения действительного решения можно взять действительную или мнимую часть полученных потенциалов.

Рассмотрим в качестве примера функцию плотности интеграла типа Коши в виде

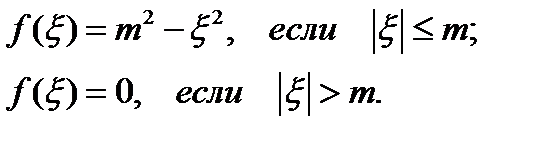
Тогда функция 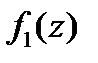будет представлена в виде

.

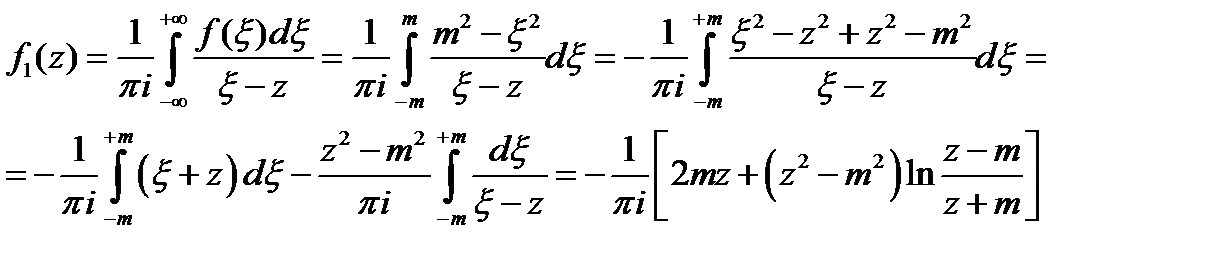Соответственно функция 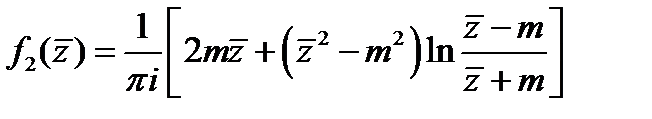. Для построения решения достаточно заменить аргументы найденных функций их значениями в согласии с (25).

Для получения действительного решения достаточно выделить действительную или мнимую часть общего решения (25).