Постоянные величины являются неизвестными амплитудными характеристиками отраженных волн (коэффициенты отражения).

После подстановки (18), (19) в граничные условия, получим следующую систему уравнений для определения :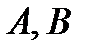

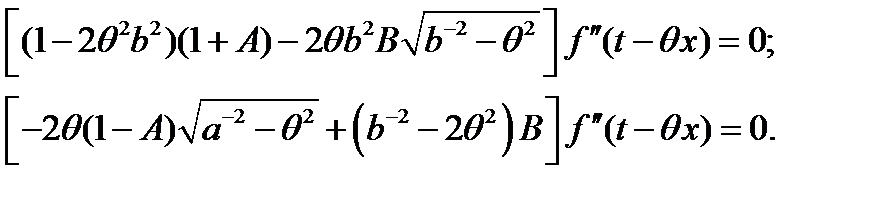(20)

Если считать вторые производные не равными нулю, можно найти коэффициенты отражения:

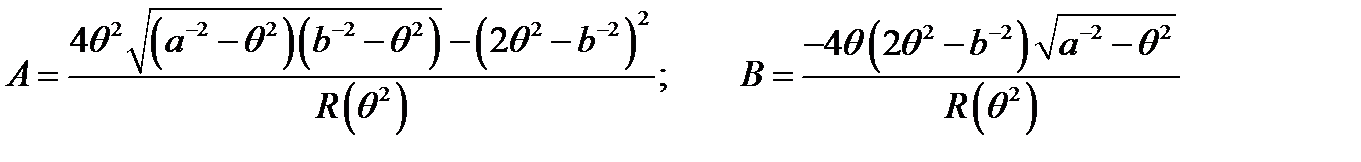, (21)

где .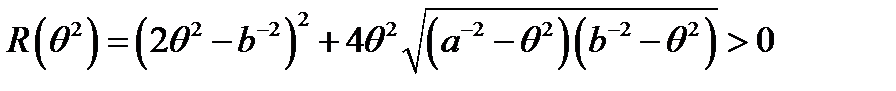

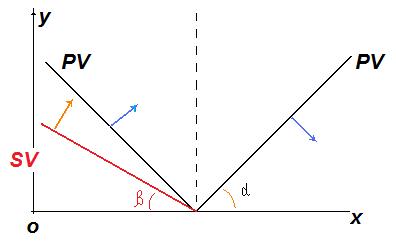
Рис.1. Падение продольной волны на свободную поверхность.

Данное решение справедливо для любых углов падения продольной волны 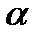, поскольку условия существования данного решения 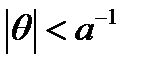, 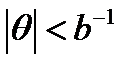выполнены для любых углов 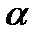(Рис.1). Действительно, согласно (16) углы падения и отражения связаны равенством

.

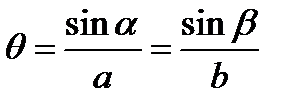Это уже известный нам закон падения отражения. Поскольку 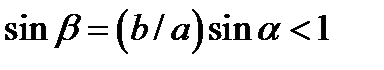, все условия существования решения выполнены.

Рассмотрим случай падения поперечной волны.Решение получается аналогично. Надо подставить потенциал падающей волны

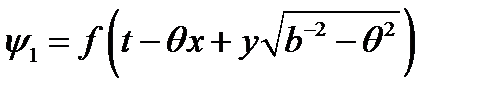
и потенциалы отраженных волн

,

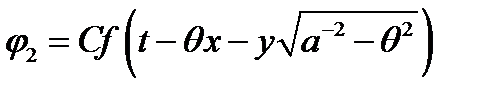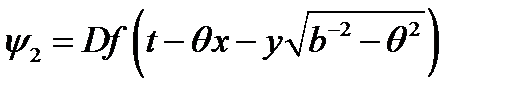
в граничные условия (17) и найти коэффициенты отражения 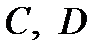. В результате получим следующие значения для коэффициентов отражения:

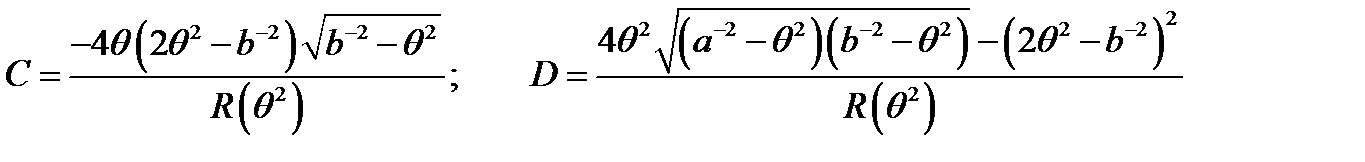. (22)

В рассматриваемом случае существует предельный угол падения 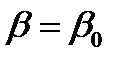, когда данное решение перестает существовать. Действительно, поскольку угол отражения продольной волны вычисляется из закона падения – отражения в виде

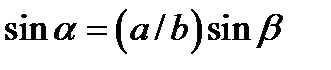, то существует критическое значение угла 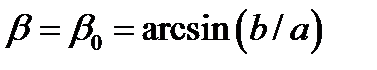, при котором 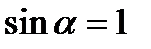. Если угол падения поперечной волны превышает данное критическое значение, то рассматриваемого решения не существует, поскольку оно существенным образом использует неравенство 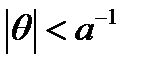. В этом случае наступает эффект так называемого «полного внутреннего отражения». Физически это соответствует наступлению такой ситуации, когда скорость движения поперечных возмущений (точка пересечения фронта поперечных волн с границей полуплоскости) оказывается равной скорости продольных волн. При превышении данного угла, продольные возмущения, возникающие в месте падения поперечной волны на границу, будут превышать скорость точки возмущений (Рис.2), (Рис.3).

Рис.2. Падение поперечной волны.

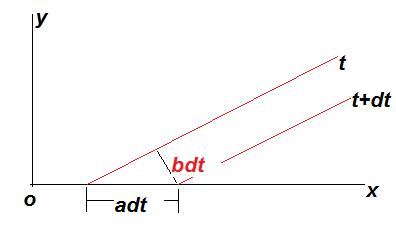
Рис.3. Переход к случаю полного внутреннего отражения.