Кинетический момент вращающегося тела
Пусть тело вращается вокруг неподвижной оси z.
Определим 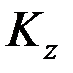 . Возьмем точку К на расстоянии hК от оси. Она будет иметь скорость, равную VК =w hК, где w – угловая скорость тела. Тогда
. Возьмем точку К на расстоянии hК от оси. Она будет иметь скорость, равную VК =w hК, где w – угловая скорость тела. Тогда 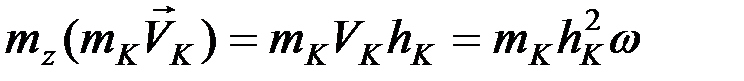 .
.
Для всего тела 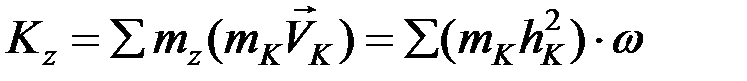 .
.
Т.к. 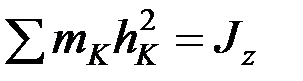 , то
, то 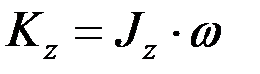 .
.
Кинетический момент вращающегося тела относительно оси вращения равен произведению момента инерции тела относительно этой оси на угловую скорость тела.
Если система состоит из нескольких тел, вращающихся вокруг одной оси, то 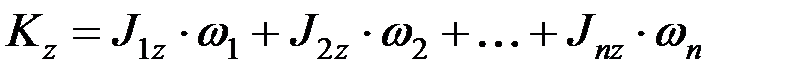 .
.
Теорема об изменении главного момента количеств движения механической системы (теорема моментов)
Теорема.Производная по времени от главного момента количеств движения системы относительно некоторого неподвижного центра равна сумме моментов всех внешних сил системы относительно того же центра.
Как было доказано для любой точки системы,
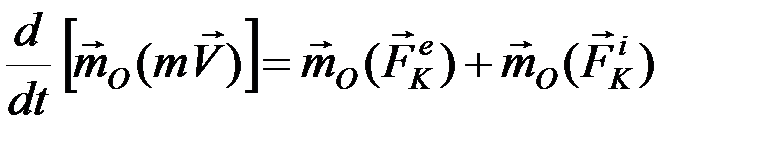 ,
,
где 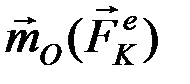 и
и 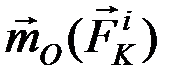 – моменты внешних и внутренних сил. Составим такие уравнения для всех точек и, складывая их почленно, получим:
– моменты внешних и внутренних сил. Составим такие уравнения для всех точек и, складывая их почленно, получим:
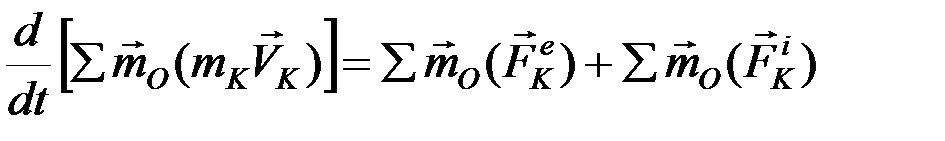 .
.
Т. к. 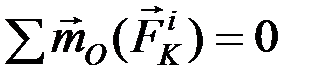 , то
, то 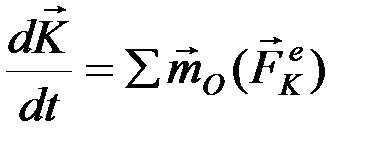 .
.
Проецируя уравнение на координатные оси, получим:
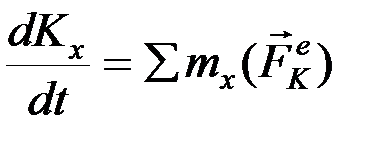 ,
,
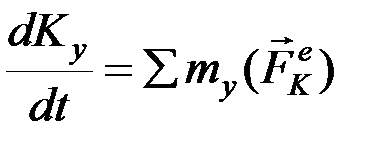 ,
,
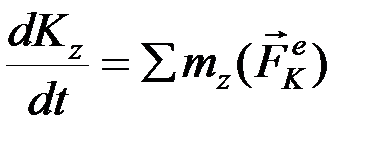 .
.
Сказанное в последних двух лекциях широко используется при решении задач. Если за полюс выбрать центр масс, то поступательная часть движения может быть изучена с помощью теорем о движении центра масс или об изменении количества движения, а вращательная – с помощью теоремы моментов.
Для осей, движущихся поступательно вместе с центром масс, теорема сохраняет тот же вид, что и относительно неподвижного центра:
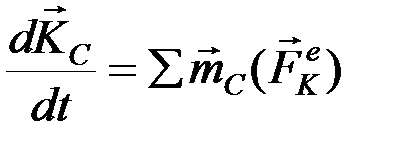 .
.
Дата добавления: 2015-12-26; просмотров: 2635;
