Лекция 10 ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ
Количество движения точки и механической системы и
его вычисление через скорость центра масс.
Теоремы об изменении количества движения точки и системы
Количеством движения материальной точки называется векторная величина 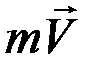 , равная произведению массы точки на вектор ее скорости.
, равная произведению массы точки на вектор ее скорости.
Единица измерения 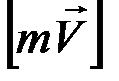 – кг·м/с или Н·с.
– кг·м/с или Н·с.
Элементарным импульсом силы называется векторная величина 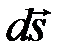 , равная произведению вектора силы
, равная произведению вектора силы 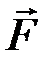 на элементарный промежуток времени
на элементарный промежуток времени 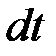 :
:
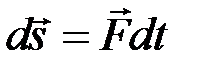 Þ
Þ 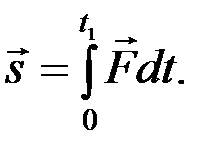
Импульс силы за некоторый промежуток времени t1 равен определенному интегралу от элементарного импульса, взятому в пределах от 0 до t1. Если сила F постоянна по модулю и направлению, то 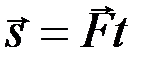 . В общем случае модуль
. В общем случае модуль 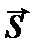 может быть вычислен по его проекциям на координатные оси:
может быть вычислен по его проекциям на координатные оси:
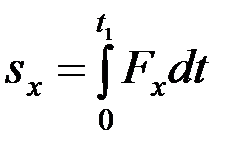 ;
; 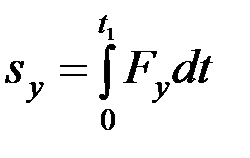 ;
; 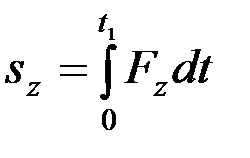 .
.
Единица измерения [s] – Н×с = кг·м·с/с2 = кг·м/с.
По второму закону Ньютона,
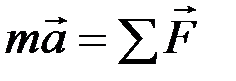 ,
,
а т.к. 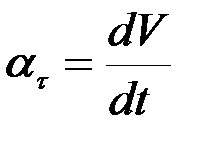 , то
, то 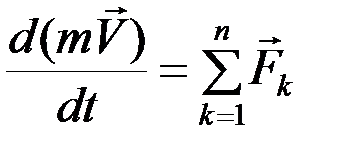 .
.
Таким образом, теорема об изменении количества движения материальной точки в дифференциальной форме формулируется в следующем виде: производная по времени от количества движения точки равна сумме действующих на нее сил.
Умножим обе части равенства на dt и проинтегрируем:
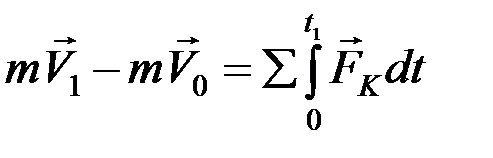
или
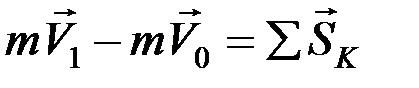 .
.
Теорема об изменении количества движения материальной точки в интегральной форме: изменение количества движения за некоторый промежуток времени равно сумме импульсов всех действующих на точку сил за тот же промежуток времени.
Количеством движения механической системы называется векторная величина  , равная геометрической сумме (главному вектору) количеств движения всех точек системы:
, равная геометрической сумме (главному вектору) количеств движения всех точек системы:
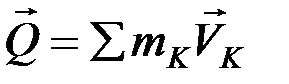 .
.
Радиус-вектор центра масс:
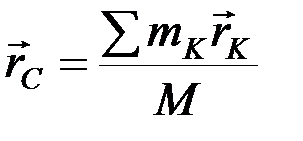
или
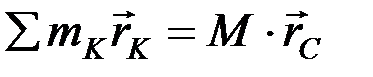 .
.
Продифференцируем левую и правую части этого уравнения по времени:
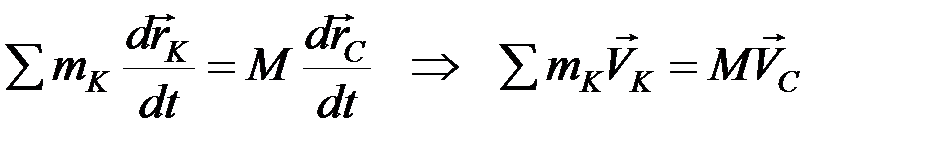 .
.
Следовательно, 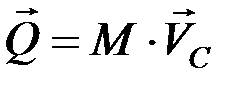 .
.
Количество движения системы равно произведению массы всей системы на скорость ее центра масс.
Очевидно, что при VC = 0, Q = 0, например, при вращении тела относительно оси, проходящей через центр масс тела.
Если движение тела сложное или плоскопараллельное, то количество движения Q не зависит от вращательного движения вокруг центра масс (например, колесо катится по рельсу). Количество движения – характеристика поступательного движения тела, а при сложном движении – характеристика поступательной части движения вместе с центром масс.
Рассмотрим систему из n материальных точек. Составим уравнения движения для каждой точки и сложим их:
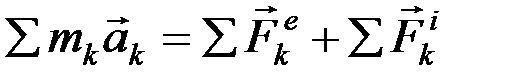 .
.
Т.к. 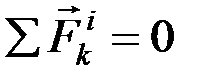 (свойство внутренних сил), то
(свойство внутренних сил), то
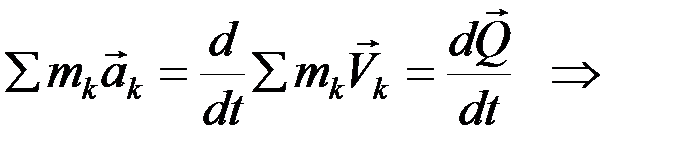
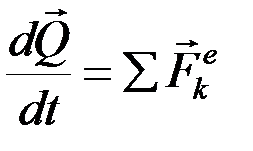 . (1)
. (1)
Производная по времени от количества движения системы равна геометрической сумме всех действующих на систему внешних сил.
В проекциях на оси координат выражение (1) записывается в виде:
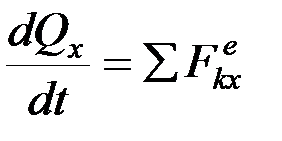 ,
, 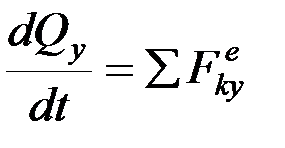 ,
, 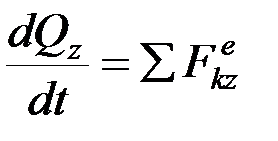 .
.
Разделив переменные и взяв интеграл, получим запись теоремы об изменении количества движения в конечной форме:
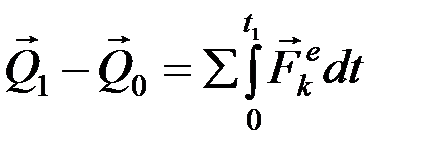
или
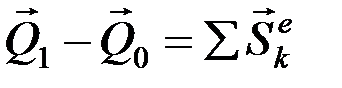 . (2)
. (2)
В проекциях на координатные оси выражение (2) записывается в виде:
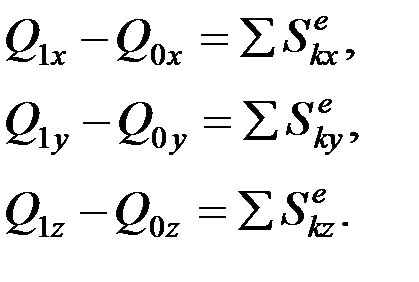
При решении задач о движении твердого тела удобнее пользоваться теоремой о движении центра масс 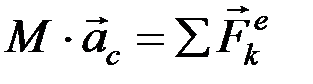 . Однако в задачах с газами, жидкостью, реактивным движением и ударом целесообразнее пользоваться теоремой об изменении количества движения
. Однако в задачах с газами, жидкостью, реактивным движением и ударом целесообразнее пользоваться теоремой об изменении количества движения 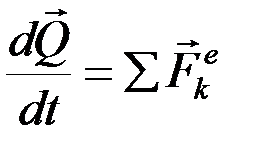 .
.
Дата добавления: 2015-12-26; просмотров: 1340;
