Теорема о движении центра масс механической системы

Допустим, наша система совершает некоторое движение, при этом центр масс будет перемещаться в пространстве. Известно, что все силы можно разделить на внутренние и внешние (в данном случае это удобнее, чем деление сил на заданные и реакции связей). Обозначим равнодействующие внешних (индекс e) и внутренних (индекс i) сил через 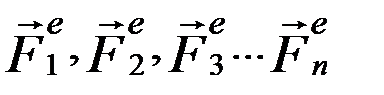и .

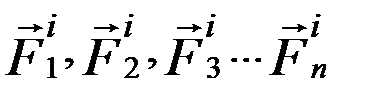Умножив обе части равенства (2) на М, будем иметь:

.

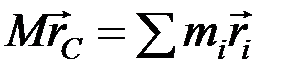Продифференцируем дважды по времени t:

.

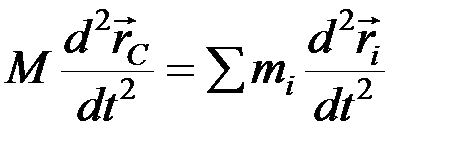Т.к. вторая производная от радиуса-вектора по времени есть ускорение а, запишем:

.

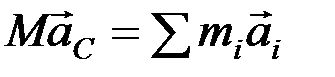С другой стороны, написав основное уравнение динамики для точки m_i, имеем:

.

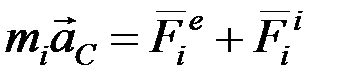Следовательно,

.

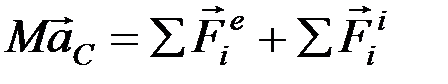Заметим, что 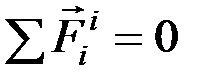, т.к. система внутренних сил твердого тела всегда уравновешена, тогда

.

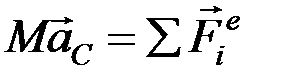Это уравнение имеет вид основного уравнения динамики для материальной точки, находящейся под действием внешних сил. Отсюда следует закон движения ЦИ: центр инерции системы движется как материальная точка, в которой сосредоточена масса всей системы и к которой приложены все внешние силы.

Проецируя уравнение на координатные оси, получим:

, , .

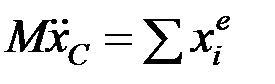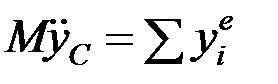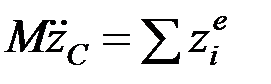Это дифференциальные уравнения движения центра масс.

Значение доказанной теоремы состоит в следующем:

1. Теорема дает обоснование использования методов динамики точки при рассмотрении системы, т.е. решение, которое мы получаем, рассматривая тело как материальную точку, определяет закон движения центра масс этого тела.

Поступательно движущееся тело всегда можно рассматривать как материальную точку.

2. Теорема позволяет при определении закона движения центра масс любой системы исключать из рассмотрения все неизвестные внутренние силы. В этом и состоит ее практическая ценность.