Изгибающие моменты и напряжения изгиба от центробежных сил. Компенсация напряжений изгиба от газодинамических сил напряжения изгиба от центробежных сил

Для обеспечения работоспособности рабочих лопаток необходимо минимизировать действующие на них нагрузки.

Изгибающие моменты от газодинамических сил можно частично компенсировать действием противоположным по знаку изгибающих моментов от центробежных сил. Для этого при построении рабочих колес предусматривают вынос центров тяжести сечения лопаток как в осевом, так и в окружном направлениях.

Степень разгрузки лопаток от изгиба характеризуется коэффициентом компенсации γ:

γ = М_y / M_г , (12)

где М_y и М_г – моменты, действующие на лопатку и обусловленные центробежными и газодинамическими силами соответственно.

Для вычисления γ необходимо определить изгибающий момент от центробежных сил в сечении с радиусом R (рис. 2.11.).

Выдели на радиусе r > R элемент лопатки высотой dr, выносы центра тяжести этого элемента (отклонение центра тяжести от оси r) равны x и y. Выносы центра тяжести сечения на радиусе R = x_i, y_i.

На выделенный элемент пера лопатки действует центробежная сила

dР_Ц = dm ∙ r ∙ ω² (13)

где dm – масса выделенного элемента;

ω – угловая скорость вращения рабочего колеса;

r – радиус.

Поскольку масса выделенного элемента равна ρ ∙ F(r) ∙ dr формула (13) приобретет вид:

dР_Ц = r ∙ ρ ∙ ω² ∙ F(r) ∙ dr (14)

В плоскости вращения roy (r – радиус, o – центр координат, y – ось) изгибающий момент дают две составляющие dР_Ц направления осей r и y.

dР_{Ц r} = dР_Ц ∙ cosα (15)

dР_{Ц y} = dР_Ц ∙ sinα (16)

Поскольку угол α мал, будем считать, что cosα ≈ 1, а sinα ≈ α = y/r.

Тогда формулы (15) и (16) можно переписать в виде:

dР_{Ц r} ≈ dР_Ц = ρ ∙ ω² ∙ F(r) ∙ r ∙ dr (17)

dР_{Ц y} ≈ dР_Ц ∙ y/r = ρ ∙ ω² ∙ F(r) ∙ y ∙ dr (18)

В результате элементарный изгибающий момент от центробежной силы относительно оси x можно определить по формуле:

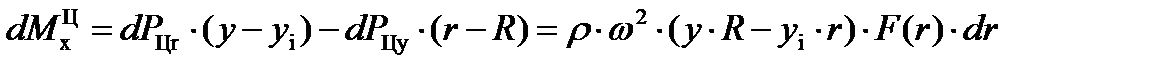(19)

В плоскости rox изгибающий момент дают радиальные составляющие dР_Ц; элементарный изгиб момента относительно оси y.

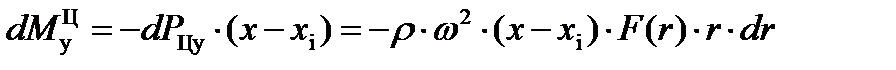(20)