Изгибающие моменты и напряжения изгиба от газодинамических сил
Для расчета напряжений используется стержневая модель лопатки. Перо лопатки считается стержнем переменного сечения, консольно закрепленным в диске. Распределенное по поверхности пера давление газа приводится к продольной оси стержня в виде интенсивности газовой нагрузки dP/dr, где P – газовая нагрузка (погонной нагрузки, приведенной к единице длины пера), изменяющейся только по высоте лопатки.
Интенсивность газовой нагрузки Р имеет две составляющие: осевую Ра и окружную Рu.
На рис. 2.6. изображены усилия, действующие на элементы рабочей лопатки компрессора и турбины при их обтекании потоком воздуха (газа).
Изменяющийся закон сохранения количества движения для движущей среды, получим выражение для интенсивности осевой (Ра) и окружной (Рu) нагрузок.
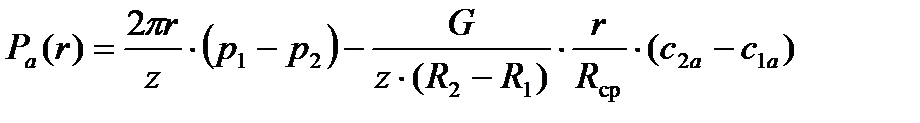(1)
(2)
где G – массовый расход воздуха [кг/с];
p1, p2 – давление газа перед и за лопаткой;
с1а, с2а – осевые составляющие абсолютной скорости газа перед лопаткой и за лопаткой;
с1u, с2u – окружные составляющие абсолютной скорости газа;
z – количество лопаток;
R1, R2 – минимальный (R1) и максимальный (R2) радиусы пера лопатки;
Rср =( R1+ R2)/2 – средний радиус лопатки.
Осевая нагрузка для рабочих лопаток компрессора направлена против потока воздуха для лопаток турбины по потоку газа. Направление окружной нагрузки для рабочих лопаток турбин совпадает с направлением вращения ротора, для компрессора – противоположно направлению его вращения.
В приближенных расчетах интенсивность газовой нагрузки можно принять постоянной по высоте лопатки и равной интенсивности на среднем радиусе. Тогда формулы для Ра и Рu упрощаются и принимают вид:
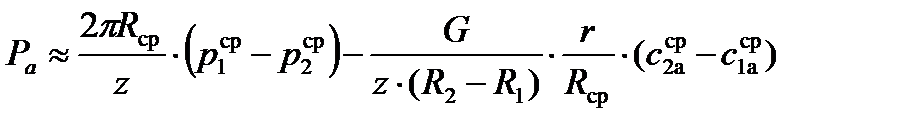(3)
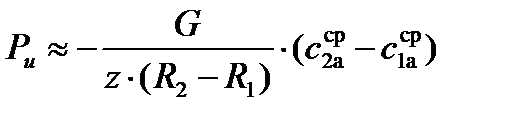(4)
Схема нагружения рабочих лопаток газодинамическими силами в плоскостях rox, roy показана на рис. 2.7.
Изгибающие моменты в произвольном сечении определяются интегрированием элементарных изгибающих моментов по радиусу лопатки. В плоскости вращения roy изгибающий момент от газодинамических сил обозначим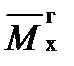 
, в плоскости rox 
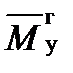. По правилу знаков для изгибающих моментов положительным считается момент, стремящийся повернуть систему по часовой стрелке, если смотреть в направлении соответствующей оси.
В произвольном сечении лопатки с радиусом r выделим элемент пера длиной (dr). Изгибающие моменты, которые создает этот элемент в сечении с радиусом R
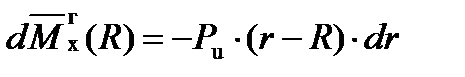(5)
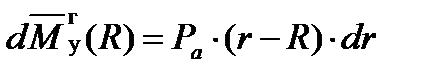(6)
Изгибающие моменты от всех элементов пера лопатки определяются интегрированием:
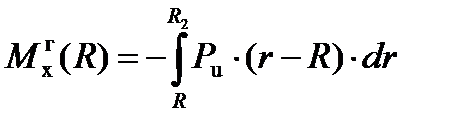(7)
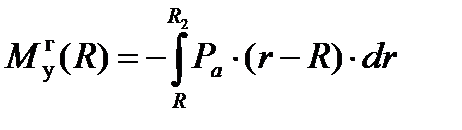(8)
Характер распределения изгибающих моментов показан на рис. 2.7. Максимальное значение приходится на корневое сечение.
Для определения напряжения изгиба в лопатках необходимо перейти к главным центральным осям рассматриваемого сечения (рис. 2.8.).
Ось минимальной жесткости сечения ξ направлена параллельно хорде сечения лопатки, ось максимальной жесткости η – перпендикулярно ей.
Угол между осью вращения ротора и осью минимальной жесткости обозначим β. Положительное направление оси ξ от входной кромки к выходной, оси η – от корыта к стенке лопатки. Максимальные напряжения изгиба возникают в точках профиля наиболее удаленных от главных центральных осей, в точках А и С, выходной и входной кромках лопатки и в точке В на спинке лопатки (рис. 2.8.).
Изгибающие моменты относительно главных центральных осей определяются путем проекции изгибающих моментов Мг x и Мг y на оси ξ и η.
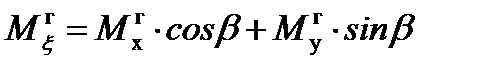(9)
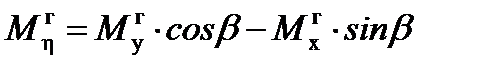(10)
В формулах (9) и (10) знаки соответствуют случаю нагружения рабочей лопатки в турбине. Для рабочей лопатки компрессора соответствующие знаки получаются, если изгибающие моменты подставить со своими знаками.
Напряжения изгиба в характерных точках профиля А, В и С определяются по формулам сопромата для случая косого изгиба через составляющие изгибающего момента Мг ξ и Мг η.
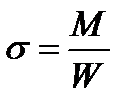
W– момент сопротивления инерции сечения Jξи Jηи координаты этих точек относительно осей ξ и η.
Для точки А выражение для расчета напряжений изгиба от газодинамических сил имеет вид:
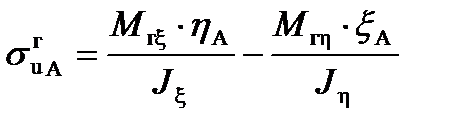(11)
Знак минус перед вторым со слагаемым означает, что положительный момент Mг ηв точке А с положительной координатой вызывает напряжение сжатия. Аналогично выглядит выражение для напряжения изгиба в точках В и С.
Моменты инерции сечения лопатки определяются по следующим формулам:
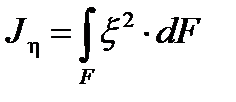
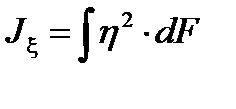
dF= b ∙ dη
Поскольку линии, ограничивающие поперечные сечения лопатки, как правило, имеют сложную форму и не всегда могут быть описаны аналитической формой, моменты инерции определяются численным интегрированием с использованием координат точек профиля.
Момент инерции Jξотносительно оси ξ пропорционален третьей степени толщины профиля; η – третьей степени хорды профиля. Поскольку толщина профиля значительно меньше его хорды, первое слагаемое в формуле (11) заметно больше второго. Напряжения газодинамических сил, действующие на рабочие лопатки турбины и компрессора, показаны на рис. 2.10. из рисунки видно, что и в лопатках турбины и в лопатках компрессора газодинамические силы вызывают появление растягивающих напряжений на входной и выходной кромках (А и С) и напряжения сжатия на спинках в точке В. Как и изгибающие моменты напряжения изгиба в рабочих лопатках максимальны по абсолютному значению вблизи корневого сечения (рис. 2.10.в). Периферийные сечения от напряжений изгиба разгружены.
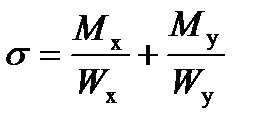– формула для расчета напряжений при косом изгибе.
Дата добавления: 2015-12-26; просмотров: 1981;