Статическая прочность дисков и дисковых элементов роторов авиационных ГТД
Статические нагрузки, действующие на диски
Центробежные силы, приложенные к собственной массе диска и к массе рабочих лопаток – вызывают напряжения растяжения;
Газодинамические нагрузки, приложенные к рабочим лопаткам и боковым поверхностям диска – вызывают изгибающие и окружные напряжения;
Температурные нагрузки из – за различия температуры по радиусу диска - вызывают напряжения растяжения и сжатия;
Температурные нагрузки из – за различия температуры по толщине диска – вызывают напряжения изгиба;
Крутящий момент, передающийся диску от вала ротора (в случае компрессора) и крутящий момент, передающийся валу от диска (в случае турбины) – вызывает окружные напряжения.
Основное назначение диска турбины состоит в передаче крутящего момента от рабочих лопаток на вал ротора, а диска компрессора – в передаче крутящего момента с вала ротора к рабочим лопаткам. Однако вызываемые этими моментами напряжения не велики по сравнению с напряжениями от центробежных сил и неравномерного нагрева, поэтому при прочностном расчете диска этими нагрузками можно пренебречь. Таким образом, в качестве основных нагрузок рассмотрим центробежные силы и неравномерный нагрев полотна диска в радиальном направлении.
В качестве расчетного режима можно использовать режим максимальной частоты вращения диска (ротора), т. е. взлетный режим (или чрезвычайный, если он предусмотрен для соответствующего двигателя). Для того, чтобы упростить задачу введем следующие допущения:
- толщина диска мала по сравнению с его диаметром;
- диск симметричен относительно его срединной поверхности, перпендикулярной оси вращения;
- температура материала диска изменяется только по радиусу и не меняется по толщине диска;
- контурная нагрузка от центробежной силы, приложенной к лопаткам, распределена равномерно по наружной поверхности диска.
С учетом принятых допущений рассматриваемый диск находится в плоском напряженном состоянии, т.е. мы имеем двумерную прочностную задачу.
Рассмотрим условия равновесия бесконечно малого элемента диска, выделенного двумя плоскостями, проходящими через ось вращения диска с углом раствора между ними dφ и двумя цилиндрическими поверхностями с радиусами r и r + dr. К выделенному элементу приложены:
1. Центробежная сила
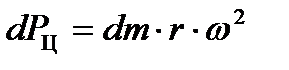 ;
;
2. Поверхностные силы, действующие в цилиндрических сечениях:
- по внутренней грани:
 ,
,
- по наружной грани:
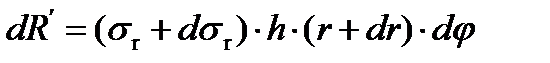 .
.
3. Силы, действующие в радиальных сечениях:
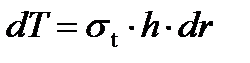 .
.
Сумма проекций всех сил, приложенных к элементу диска, на радиальное направление должна быть равна нулю (условие равновесия):
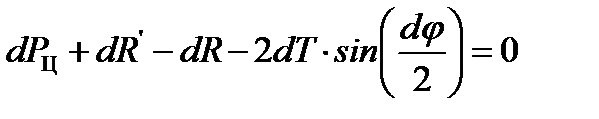 (1)
(1)

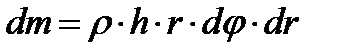
В виду малости угла dφ считаем
 .
.
Подставляя значение слагаемых в уравнение (1), получим:
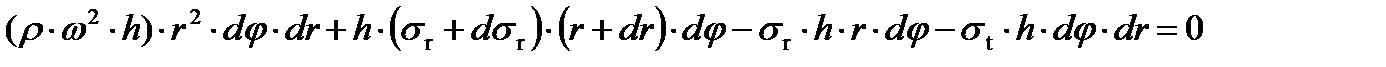 (2)
(2)
 (3)
(3)
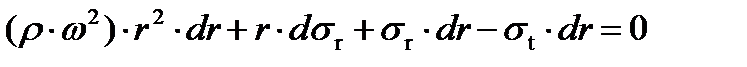 (4)
(4)
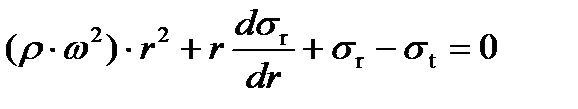 (5)
(5)
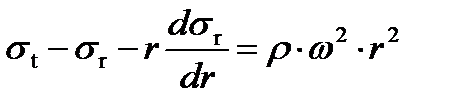 (6)
(6)
В итоговом дифференциальном уравнении (6) содержатся две неизвестные функции, зависящие от переменной r:  и
и 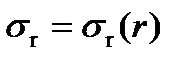 , поэтому необходимо составить еще одно дифференциальное уравнение – уравнение совместности деформаций.
, поэтому необходимо составить еще одно дифференциальное уравнение – уравнение совместности деформаций.
Уравнение совместности деформаций составим с учетом воздействия центробежных сил на полотно диска. Пусть y – перемещение нижней грани элемента диска в радиальном направлении; dy – перемещение (удлинение боковой грани элемента диска) в радиальном направлении (увеличение радиального размера элемента); y + dy – перемещение верхней грани элемента диска в радиальном направлении. Относительная деформация боковой грани элемента в радиальном направлении:
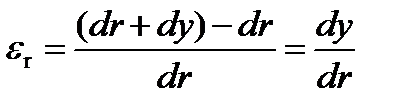 .
.
Относительная деформация внутренней грани элемента в окружном направлении:
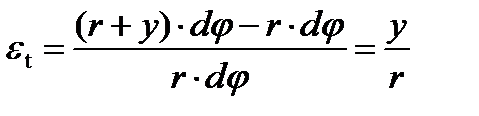 .
.
Отсюда 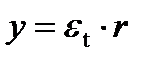 .
.
Дифференцируя y по r, получим:
 .
.
Подставляя значение для 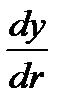

Закон Гука для двумерного напряженного состояния
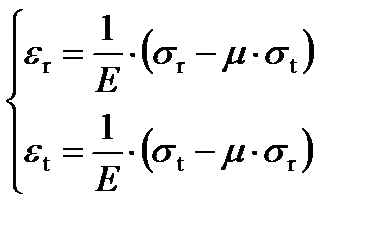
Взяв производную от левой и правой частей второго уравнения в законе Гука, получим:
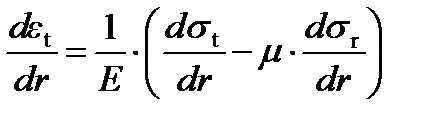
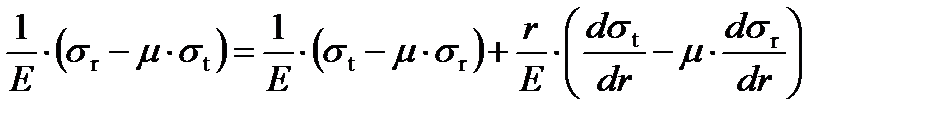
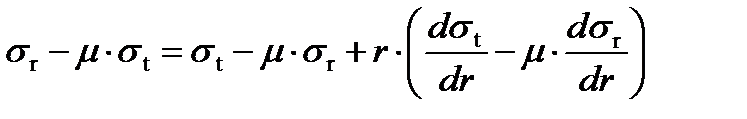
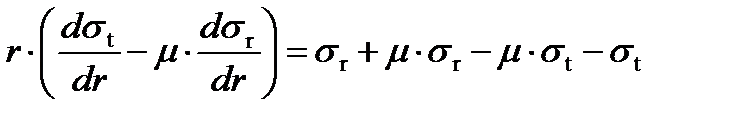

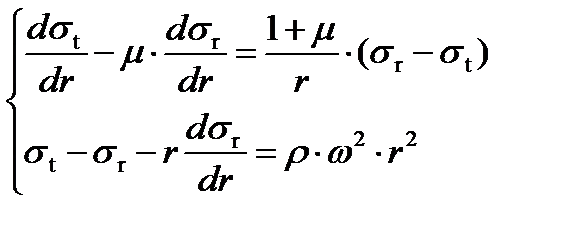
1. Если мы хотим определить зависимости для напряжений 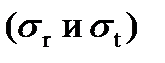 в случае действия центробежной силы на массу самого диска, то должны использовать следующие граничные условия:
в случае действия центробежной силы на массу самого диска, то должны использовать следующие граничные условия:
при r = R1, σr = 0;
при r = R2, σr = 0.
При этих граничных условиях полученная нами система обыкновенных дифференциальных уравнений имеет следующее решение:
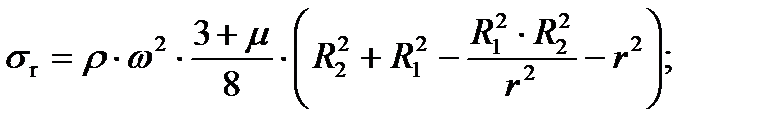
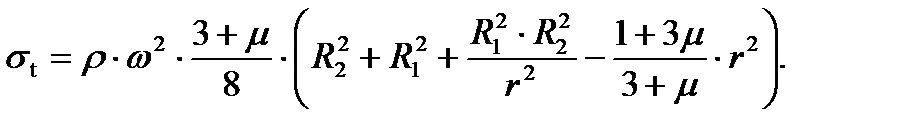
2. Случай действия центробежной силы, приложенной к рабочим лопаткам и ободу диска (случай действия только контурной нагрузки).
Дифференциальные уравнения равновесия в этом случае изменятся (dPЦ = 0), а уравнение совместности деформаций останется прежним.
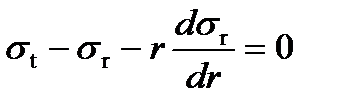
Для получения граничных условий необходимо задать распределенную контурную нагрузку σк.
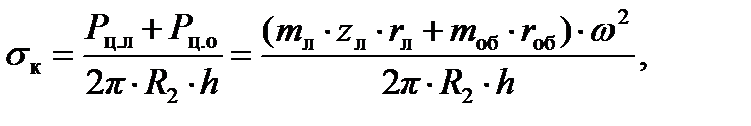
где Pц.л – суммарная центробежная сила, приложенная к рабочим лопаткам;
Pц.о – центробежная сила, действующая на обод диска;
R2 - наружный радиус диска;
h – толщина диска;
mл – масса лопатки;
zл – количество лопаток;
rл – радиус центра масс лопатки (rл > R2);
mоб – масса обода;
rоб – радиус центра масс элементов обода;
ω – угловая скорость вращения диска.
Граничные условия для рассматриваемого случая нагружения:
при r = R1, σr = 0;
при r = R2, σr = σк.
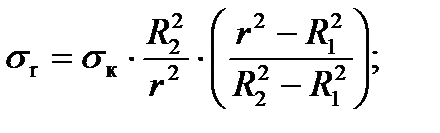
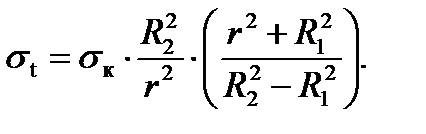
3. Случай температурных напряжений.
Определим зависимости для напряжений 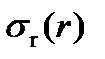 и
и 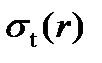 , возникающих вследствие неравномерного нагрева диска по радиусу. Исходная система дифференциальных уравнений для этого случая – это уравнение равновесия и уравнение совместности деформаций (записанные для относительных деформаций).
, возникающих вследствие неравномерного нагрева диска по радиусу. Исходная система дифференциальных уравнений для этого случая – это уравнение равновесия и уравнение совместности деформаций (записанные для относительных деформаций).
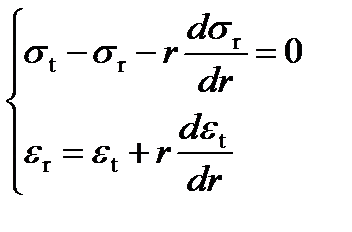
Запишем закон Гука для плоского напряженного состояния с учетом неравномерного нагрева:

Для того, чтобы учесть воздействие неравномерного нагрева, нужно добавить в правые части уравнений закона Роберта Гука слагаемые, описывающие относительную деформацию материала под действием нагрева, а именно – α ∙ T, где α – коэффициент линейного расширения материала диска, Т – температура диска.
Кроме того, потребуется закон изменения температуры диска по радиусу. Для охлаждаемых дисков этот закон близок к квадратичной зависимости. После проведения преобразований, аналогичных расчету напряжений σr и σt в предыдущих случаях, получим следующую систему уравнений:
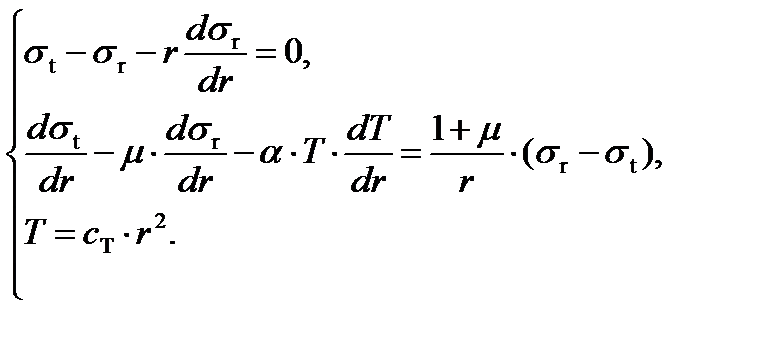
Граничные условия:
при r = R1, σr = 0, Т = Т1;
при r = R2, σr = 0, Т = Т2.
Решение системы уравнений имеет вид:

Получив значения напряжений σr и σt от трех рассмотренных факторов нагружения диска для любого значения радиуса r, можем определить суммарные напряжения
?
Поскольку напряжения σr и σt направлены под прямым углом друг к другу, то мы должны определить эквивалентные напряжения (в соответствии с теорией наибольшей энергии формоизменения).
Запас по местной прочности диска определяется следующим образом:
?
– предел длительной прочности материала диска.
Помимо расчетов статической прочности основных «критичных» элементов авиационных ГТД (рабочих лопаток и дисков) такие расчеты выполняются и для всех остальных деталей двигателя:
– элементов статоров, включая: корпуса, детали подвески двигателя, опоры роторов, лопатки НА, детали камеры сгорания;
– выходных и реверсивных устройств;
– зубчатых передач центрального привода, коробок приводов агрегатов, редукторов турбовинтовых и вертолетных двигателей (а в последнее время – и редукторов вентиляторов ТРДД);
– элементов пусковых устройств и др.
Дата добавления: 2015-12-26; просмотров: 1935;
