Использование теории игр для анализа олигополии
Кооперативные и некооперативные стратегии олигополистов обстоятельно анализируются в рамках теории игр, которая исследует математическими методами поведение экономических агентов в вероятностных ситуациях принятий решений.
Теория игр получила широкое распространение в экономической науке, о чем свидетельствует то, что с 1994 г. четверть нобелевских лауреатов (8 из 33) по экономике получили премии «за осмысление конфликта и сотрудничества посредством анализа теории игр», «за работы по теоретико-игровому анализу конкурентного поведения».
Теория игр в экономических исследованиях начала использоваться практически с момента ее появления, т.к. первой фундаментальной работой стала «Теория игр и экономическое поведение» Д. фон Неймана и О. Моргенштерна (1944 г.). Ее авторы понимали игру как любое взаимодействие между агентами, которое регулируется правилами, определяющими возможные действия каждого участника, и предполагающее систему выигрышей для всех допустимых комбинаций решений.
Неоклассический подход решений проблем экономического выбора сводится к определению оптимального варианта использования ограниченных ресурсов – максимизация целевой функции (выработка, прибыль, полезность) при известных ресурсных (бюджетных) ограничениях. Математический аппарат для решения таких задач – дифференциальное и вариационное исчисление. Но для моделирования взаимодействий экономических субъектов, когда каждый субъект выбирает стратегию поведения, учитывая возможные влияния такой стратегии на других субъектов и их вероятные реакции, нужен уже другой математический аппарат, аппарат теории игр. Игрой называется ситуация, характеризующаяся: 1) наличием множества агентов (игроков), у каждого их которых имеется множество альтернативных линий поведения или стратегий; 2) наличием исходов, зависящих от комбинаций действий игроков и определяющих предпочтения игроков на множестве этих комбинаций; 3) тем, что каждый игрок знает, каковы эти предпочтения у всех других игроков, и знает, что они известны всем остальным.
Экономическую теорию можно определить как теорию рационального выбора, а теорию игр как ее составную часть – теорию стратегического поведения.
При рассмотрении олигополистических рынков, модели олигополии могут быть представлены в форме игры, действий и стратегий по установлению цен, размеров выпуска, определению издержек. Олигополистические игры предполагают наличие двух (дуополия) или нескольких фирм, стремление каждой из них к максимизации своей прибыли в условиях воздействия со стороны остальных.
Описание конкретной игры включает перечень ее участников, их возможные действия (хода или стратегии), набор функций выигрыша (платежи, выплаты) для каждого игрока обычно в виде платежной матрицы (матрицы выигрышей). Это так называемая игра с полной информацией в нормальной форме (нормальная игра).
Различаются игры с двумя, тремя и более участниками. По свойствам функции выигрыша или степени гармонии (взаимодействия) различают игры с нулевой суммой, с постоянной разницей, а также кооперативные и некооперативные игры.
Игры с нулевой суммой (антагонистические), когда выигрыш одного игрока равен проигрышу другого. Здесь налицо прямой конфликт интересов, предпочтения игроков в отношении стратегии противоположны и нет никаких причин для сотрудничества (кооперативных действий).
Игры с постоянной разностью, в которых игроки и выигрывают, и проигрывают одновременно, требуют совместных действий. В зависимости от возможности предварительных переговоров между игроками различают кооперативные и некооперативные игры. В кооперативной игре до ее начала образуются коалиции и принимаются взаимообязующие соглашения о стратегиях, направленных на максимизацию общего выигрыша, который затем распределяется между участниками. В некооперативных играх игроки не могут координировать свои стратегии, не создают коалиции и стараются максимизировать только свой индивидуальный выигрыш.
Важным элементом игры является структура информации. В играх с полной информацией предполагается, что общеизвестны множество стратегий игроков, их функции выигрыша. В играх с асимметричной информацией – а они наиболее распространены и отражают экономические реальности – какая-то часть информации считается общедоступной, известны также вероятностные значения каких-то показателей, но часть информации о предыдущих действиях, о функции выплат, о функции издержек и ценовой стратегии конкурентов неполна или неизвестна ЛПР (лицам, принимающие решения) данной фирмы.
Различают также однопериодные (статические) игры, где игроки сталкиваются однократно, их стратегия задана начальными условиями и не меняется (они характерны для дуополии), и многопериодные (динамические) игры, где «время и история игры имеют значение», стратегия меняется. В динамичных играх игроки могут вести предварительные переговоры для «корректирования стратегий». Стратегический ход в динамической игре – это действие, которое влияет на выбор соперника в сторону, благоприятную для данного игрока, воздействуя на ожидания соперника относительно его действий. Средства такого воздействия правдоподобные (это очень важно!) обязательства, угрозы, обещания, «инвестиции в дезинформацию» (ложные сигналы, блефы и т.д.).
Основные правила и этапы построения моделей игр (А. Шаститко, 2002 г., А. Сергеев, 2006 г.):
1. Индификация ЛПР, т.е. игроков (потребитель, предприниматель, политик).
2. Определение действий (ходов), которые совершат игроки и которые составляют их стратегию.
3. Способность создания коалиций – группы игроков, которые могут давать заслуживающие доверия обещания для реализации согласованных стратегий.
4. Конструирование нормальной игры на основе информации о выигрышах – составление матрицы игры.
5. Установление объема информации о возможных стратегиях, которой обладают игроки.
Решением игры является определение набора равновесных стратегий. Из возможных во взаимодействиях игроков равновесий выделяются: а) равновесие доминирующих стратегий; б) равновесие Нэша.
Доминирующей стратегией называется такой план действий, который обеспечивает участнику максимальную полезность вне зависимости от действий других участников. Соответственно равновесием доминирующих стратегий будет пересечение доминирующих стратегий все игроков.
Равновесием Нэша называется выбор рациональных стратегий при взаимодействии множества игроков, который будет устойчивым, но не обязательно наилучшим (Парето-оптимальным). Это равновесие представляет собой ситуацию, в которой стратегия каждого из игроков является наиболее выгодным ответом на действия других игроков. В случае игры с двумя участниками (к которой в принципе можно свести игру любой степени сложности) пара стратегий (α*, β*) называется равновесием Нэша (некооперативным равновесием) тогда, когда каждая из них есть наилучший ответ на другую, т.е. α* максимизирует полезность U(α, β*), а β* максимизует полезность V(α*, β). U(α, β) и V(α, β), означают платежи (выигрыши) А и В соответственно, если выбрана пара стратегии (α, β). Равновесие Нэша обеспечивает каждого игрока максимальным выигрышем в зависимости от действий другого игрока. В данном случае имеем некооперативную игру между А и В с нулевой суммой: U(α, β)= –V(α, β) и решение игры α*, β* (седловая точка) задает maxU на множестве α и minU на множестве β.
Д.Нэш в знаменитой теореме о торге (1950 г.) доказал, что существует такая область (точка) решений, когда ни один из игроков не может улучшить свое благосостояние и находится в состоянии паретооптимальноого равновесия. Свой вывод он строит на основе принятия ряда аксиом (аксиоматический торг): монотонность по допустимому множеству полезностей и составу участников, независимость от масштаба и посторонних альтернатив.
Равновесие Нэша явилось одним из фундаментальных положений теории игр. Например, нобелевский лауреат по экономике 2007 года Р. Майерсон сопоставил роль Нэша в развитии современной экономической науки с ролью для развития биологии и генетики выявление Криком и Уотсоном двойной спирали молекулы ДНК (кстати, почти в одно время с работами Нэша 1950-1951 гг.). Судьба Д.Нэша была драматичной (она показана в оскароносной голливудской ленте 2001 г. С Р. Кроу в главной роли – Beautiful mind или Игры разума): блестящий математик-вундеркинд из Принстона в 1947-1952 гг., затем длительная борьба с психологической болезнью, распадом личности, а в конце восстановление и мировое признание как нобелевского лауреата по экономике 1994 года.
В теории игр важнейшие проблемы, теоремы, леммы иллюстрируются оригинальными задачами типа «дележ агентами подарка из виски и джина», решения «раввина о наследстве вдов», «производство кукурузы в имении» и т.д. Но самой знаменитой стала «дилемма заключенных» (А. Таккер, 1955 г.), с помощью которой показывается, что доминирующая стратегия, диктуемая «принципом обеспеченного успеха» и нацеленная на наилучший результат независимо от стратегии партнера-конкурента, оказывается худшей по сравнению с кооперативным выбором.
Двое пойманы с краденными вещами и подозреваются в краже со взломом. Но для приговора за кражу со взломом (5 лет тюрьмы) нет пока оснований, т.к. они не признаются. Им можно вынести приговор за хранение краденного (полгода тюрьмы).
Их помещают в разные камеры, чтобы они не общались и шериф разъясняет им «права»: если оба признаются, то за кражу со взломом получат 2 года тюрьмы, если оба не признаются, то получать по полгода за хранение краденного. Если один признается, то не будет наказан, в то время как непризнающийся напарник получит 5 лет тюрьмы.
Доминирующая стратегия каждого из заключенных – признаться в надежде, что можно получить максимум два года при признании партнера или свободу при его непризнании. Но руководствуясь этой стратегией обеспечения успеха, оба они оказываются в худшем положении, чем при непризнании – тогда получили бы только по полгода.
В нормальном виде такая игра представляется в матричной форме 2×2: строки C1 и D1 – отказ и признание первого заключенного, а C2 и D2 – отказ и признание второго.
| Второй заключенный | |||
| признание | отказ | ||
| Первый заключенный | признание | 2; 2 | 0; 5 |
| отказ | 5; 0 | 0,5; 0,5 |
Имеем олигополистические фирмы А и В, которые выбирают из двух вариантов цен аналогичных товаров: или низкие цены по 10 долл., или высокие – 15 долл. Ежегодная прибыль (млн. долл.), ожидаемая каждой из фирм для себя и для соперника представлена в матрице нормально игры:
| Ценовая стратегия В | |||
| цена 10 долл. | цена 15 долл. | ||
| Ценовая стратегия А | цена 10 долл. | 100; 80 | 180; 30 |
| цена 15 долл. | 50; 170 | 150; 120 |
Видим, что фирма А предпочтет низкую цену в 10 долл. (100>50), фирма В также предпочитает низкую цену (80>30). Следовательно, доминантная стратегия при некооперативной игре каждой фирмы – выбор цены в 10 долл. Но если бы они заключили предварительное соглашение, вступили в коалицию, то выбрали бы высокую цену и получили дополнительно: А – 50 млн. долл., В – 40 млн. долл.
В заключении приведем примеры решения задач.
Пример 1. На рынке работают две фирмы, взаимодействующие по Курно. Средние издержки фирм не зависят от объема выпуска, равны и составляют 10. Рыночный спрос описывается формулой Р=100-5Q. Определить параметры рыночного равновесия по Курно. Найдите параметры равновесия Штакельберга, если одна из фирм становится лидером, снизив свои средние издержки до 8.
Решение: Вначале определим функции реакции фирм, максимизирующих свою прибыль и взаимодействующих по Курно. Прибыль первой из них зависит от выпуска как: π1(Q1)=[100-5(Q1+Q2)]Q1-10Q1, где Q1 – выпуск 1-й фирмы, Q2 – выпуск 2-й фирмы.
Оптимальный объем продаж фирмы 1 (Q1*) зависит от объема продаж 2-й фирмы (реакция на ее деятельность). Соответствующее уравнение получим из условия максимума функции π1(Q1), т.е. при 
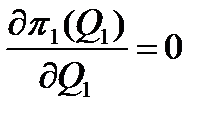 или 100-10Q1*-5Q2-10=0, т.е. Q1*=9-0,5Q2.
или 100-10Q1*-5Q2-10=0, т.е. Q1*=9-0,5Q2.
| Р*=100-5(Q2*+Q1*) Q1*=Q2*=6 9-0,5Q2*=9-0,5Q1* → P*=40 Q1*=9-0,5Q2* π1*=π2*=180 |
Если фирма 1 становится штакельбергским лидером, то для нее зависимость прибыли от объема выпуска будет такой: π1(Q1)=[100-5(Q1+(9-0,5Q1))]Q1-8Q1,и тогда оптимальный объем продаж фирмы 1: 55-5Q1*-8=0 и Q1*=9,4, Q2*=9,4/2=4,3, P*=100-5(9,4+4,3)=31,5, π1*(9,4)=220,9 и π21=92,45.
Лидер, имеющий преимущество в издержках и преимущество «первого хода», добивается увеличения прибыли за счет сокращения прибыли фирмы 2.
Пример 2. На рынке действуют две фирмы, объемы продаж которых стабильны и они делят между собой общую сумму прибыли А. Компании должны принять решение – рекламировать или не рекламировать свою продукцию. Реклама не влияет на общий спрос, а только изменяет его распределение между фирмами. Если обе фирмы выбирают одинаковую стратегию (рекламировать или нет), то они делят рынок и прибыль пополам. Если одна компания рекламирует свою продукцию, а другая – нет, то первая получит 70% продаж и прибыли, а вторая – только 30%. Издержки на рекламу составляют С. Напишите нормальную (матричную) форму статичной игры и определите равновесие Нэша при А=100 и С=10.
Решение: нормальная форма игры отображается матрицей:
| Фирма 2 | |||
| Фирма 1 | Рекламировать продукцию | Не рекламировать продукцию | |
| Рекламировать продукцию | 0,5А-С; 0,5А-С | 0,7А-С ; 0,3А | |
| Не рекламировать продукцию | 0,3А ; 0,7А-С | 0,5А; 0,5А |
Видно, если обе фирмы не рекламируют продукцию, их прибыль больше, чем в случае, когда обе фирмы ее рекламируют.
Если доминирующей стратегией для обеих фирм в их некооперативном соперничестве станет стратегия «рекламировать товар», то должны выполняться условия:
0,5А-С> 0,3А;
0,7А-С>0,5А;
Сумма расходов на рекламу должна быть меньше, чем 20% прибыли рынка.
При А=100 и С=10 матрица прибыли приобретает вид:
| Фирма 2 | |||
| Фирма 1 | Рекламировать продукцию | Не рекламировать продукцию | |
| Рекламировать продукцию | 40; 40 | 60 ; 30 | |
| Не рекламировать продукцию | 30; 60 | 50; 50 |
Равновесие Нэша в неповторяющейся игре – «рекламировать товар»
Пример 3. Отраслевой спрос задан функцией: Q=110-Р, затраты производства ТС=10Q. Найти параметры равновесия Нэша, когда в отрасли функционируют две и четыре фирмы.
Допустим, что предложение монополизировано (имеется одна фирма).
Тогда: 110-2Q=10 →Q*=50 и Р*=60.
Прибыль π=60*50-10*50=2500.
Теперь монополия разделена на две фирмы, максимизирующие прибыль:
Q1=Q2=25; P=60 π1=π2=1250.
Каждая из фирм может повысить свою прибыль за счет увеличения выпуска. Так, если Q1=26, а Q2=25, P=59 и π1=1274, а π2=1225. В ответ на это фирма 2 тоже может увеличить выпуск до Q=26. Тогда Р=58, π1=1278, π2=1248. Последующие шаги приведены в табл. 6.1:
Таблица 6.1. Установление равновесия на олигополистическом рынке по Нэшу
| Номер шага | Q1 | Q2 | P | π1 | π2 |
| … | … | … | … | … | … |
С 17 шага ни у одной из фирм нет стимула к дальнейшему увеличению выпуска, так как это сокращает абсолютную величину прибыли, т.е. при цене Р=44 устанавливается равновесие Нэша.
Если в этой отрасли 4 фирмы, то аналогичные шаги дадут следующий результат (табл. 6.2):
Таблица 6.2. Установление равновесия на олигополистическом рынке по Нэшу
| Номер шага | Q1 | Q2 | Q3 | Q4 | P | π1 | π2 | Π3 | π4 |
| … | … | … | … | … | … | ||||
Равновесие Нэша установится на 37 шаге при Q1=Q2=Q3=Q4=20 и цене равновесия Р=30.
Дата добавления: 2015-11-26; просмотров: 3821;
