Моделирование кратчайшей цепи, максимального потока в сети, кратчайшего остова-дерева интегрированной цепи
Классическим примером задачи моделирования кратчайшей цепи является нахождение связанных между собой транспортных коммуникаций на транспортной сети, которые в совокупности имеют минимальную длину от исходного пункта до пункта назначения. Однако на практике с помощью данного метода решаются различные случаи в логистических цепях, которые можно промоделировать и решить как задачу о кратчайшем пути.
Пусть задана транспортная сеть, состоящая из станций А0, А1 и т.д. и коммуникаций, соединяющих некоторые из этих станций.
Длины коммуникаций предполагаются известными и равными Cij. Если станции Аi и Аj непосредственно не соединены друг с другом, предполагаем что Сij равна бесконечности. Из начальной станции А0 на конечную станцию Аn+1 можно попасть через большое количество путей, проходящих через разные промежуточные станции. Требуется выделить из всех путей путь наименьшей длины. Поясним, что длины коммуникаций могут означать время движения, стоимость перевозок от станции до станции, вероятности своевременной перевозки груза от станции до станции и др.
Экономико-математическая модель решения задачи сводится к следующему.
Приведем в соответствии каждой паре пунктов Аi и Аj величины Хij.
Если участок АiАj принадлежит кратчайшему пути Хij=1 и, Хij =0 в противном случае. Задача о кратчайшем пути в таком случае может быть сведена к выбору чисел Хij, для которых сумма произведений длины дуг на искомые переменные Хij стремится к минимуму при условиях:
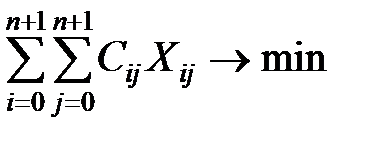 (1)
(1)
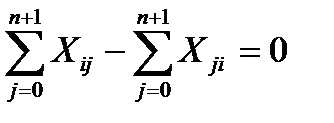 (2)
(2)
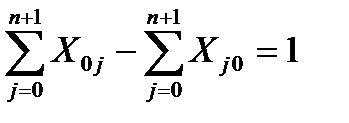 (3)
(3)
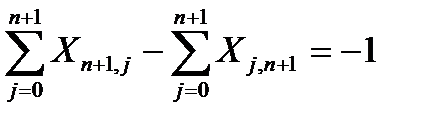 (4)
(4)
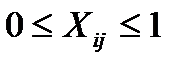 (5)
(5)
Условие 2 соответствует тому, что число коммуникаций, принадлежащих критическому пути и в ходящих в любой промежуточный пункт равно числу коммуникаций исходящих из этого пункта и принадлежащих критическому пути.
Условие 3 означает, что количество коммуникаций из исходного пункта А0 превышает на единицу число коммуникаций входящих в исходный пункт.
Аналогичным образом условие 4 свидетельствует о том, что в конечный пункт Аn+1 входит на одну коммуникацию больше, чем выходит.
Вместе с условием 2 и требованием минимизации целевой функции 1 условия 3 и 4 означают, что на каждую станцию Аi приходит ровно одна коммуникация и из каждой станции Аi исходит ровно одна коммуникация.
Условие 5 в задаче эквивалентно требованию, согласно которому все значения Хij равны нулю или единице.
Таким образом, соотношения 1-5 определяет кратчайший путь в сети. Необходимо еще раз отметить, что в качестве длин дуг могут быть не только километры, но и другие показатели, например стоимости, время, пропускную способность и т.д. Для максимизации потока в цепи поставок достаточно изменить знак целевой функции с минимума на максимум.
В задачи оптимизации цепей поставок входит решение вопросов по оптимальному размещению различного рода коммуникаций (отысканию кратчайшего остова-дерева интегрированной цепи). В различных случаях дополнительные условия размещения могут быть разными, но в большинстве ситуаций критерием оптимальности является суммарная длина размещаемых коммуникаций.
Такого рода задачи имеют общую смысловую модель: дана плоскость и на ней N объектов. Заданы расстояния между объектами. Требуется соединить объекты отрезками между собой так, чтобы суммарная длина отрезков была минимальной.
Решение задачи предусматривает следующие допущения.
1. Объекты относительно малы по сравнению с расстояниями между ними. Поэтому величиной объектов можно пренебречь и изображать их в виде точек.
2. Расстояния между объектами могут быть заданы двумя способами: в натуральном виде (как число метров, километров и т.д.) или опосредованно через задание положения объекта относительно какой-либо точки отсчета. Во втором случае вводится подходящая система декартовых координат и положение i-го объекта, где i = 1, ..., N, задается парой координат (x[i],y[i]). Условие, что страна плоская, означает, что d[i,j] (расстояние от i-го объекта до j-го) задается по формуле Пифагора (квадрат гипотенузы равен сумме квадратов катетов).
3. Подразумевается транзитивность связи: если i-й объект связан с j-м объектом, а j-й с k-м, то i-й связан с k-м.
4. Подразумевается или указано явно, что коммуникации могут разветвляться только на территории связываемых объектов.
5. И, наконец, на основе здравой логики можно утверждать, что в оптимальном решении не будет циклов. Если бы в минимальном решении был цикл, скажем, (i, j, k, l, i), то можно было бы убрать одно звено цикла, скажем, (j, k), причем связь между j и k сохранилась бы по другой стороне цикла, по пути (j, i, l, k). Но, убирая одно звено, мы бы уменьшили минимальный цикл, что невозможно.
После такой конкретизации можно вводить графовую модель, в рамках которой объекты становятся вершинами, а возможные связи между ними – ребрами. Расстояния между объектами заданы в виде таблицы – она в точности совпадает с матрицей смежности, задающей произвольный граф. В терминах теории графов такая задача независимо была поставлена и решена двумя математиками: Примом (Prim)и Краскалом (Kruskal).
Под исходной сетью будем понимать сеть из n заданных узлов, которые можно связать между собой различными физически реализуемыми соединительными линиями, называемыми ребрами сети. Распределительная сеть представляет собой сеть из n узлов, получаемую из исходной сети и содержащую по одному пути (путь состоит из последовательности ребер) из корневого узла (узел 1) в каждый из оставшихся (n-1) узлов. Задача минимизации заключается в том, чтобы из всей совокупности распределительных сетей выбрать одну, минимизированную по стоимости, а именно минимум суммарного веса ребер распределительной сети, соответствующий минимуму затрат на развертывание распределительной сети. Сущность методики заключается в модификации алгоритма Дейкстры выбора кратчайшего пути в сетях с коммутацией пакетов. При реализации процедуры оптимизации по разработанному алгоритму используются следующие параметры распределительной сети:
n — число узлов распределительной сети;
D(k) — вес пути (сумма весов рёбер вдоль данного пути) от корневого узла 1 до узла k;
l(m, k) — вес ребра между m-м и k-м узлами;
N — множество, элементами которого являются номера узлов, добавляемые на каждом шаге алгоритма оптимизации на основе вычисления путей с минимальным весом.
Процедура нахождения минимальной цепи включает конечное множество шагов.
Начальный шаг. Формируется исходное множество N = {1}, D0(1) = 0. Для каждого узла k, не принадлежащего множеству N, устанавливается D0(k) = l(1, k). Формируется множество начальных путей вида Р0(k) = [1_k], где в квадратных скобках указаны номера узлов, образующих маршрут.
Каждый последующий i-й шаг (i=1,2…,n-1) значения Di(k) обновляются для всех узлов, не принадлежащих множеству N. Среди обновлённых значений Di(k) выбирается минимальное, а соответствующий ему узел m включается во множество N. На основании значений Di(k) производится обновление путей Рi(k). Процедура повторяется, пока во множество N не войдут все узлы исходной сети.
Дата добавления: 2015-12-22; просмотров: 1265;
