Законы излучения абсолютно чёрного тела

Обсуждаемые ниже законы излучения справедливы в полной мере только для абсолютно чёрных тел (частично для абсолютно серых тел) и являются универсальными независимо от вещества АЧТ, способа его обработки и т.д.

1. Закон Планка

Известно, что любое твёрдое макроскопическое тело, температура которого отличается от абсолютного нуля (–273.15^оС), излучает электромагнитные волны с длинами теоретически от нуля до бесконечности. Энергия излучаемых телом волн различна для различных длин волн. Энергия излучения 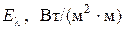, приходящаяся на единицу площади излучающей поверхности и на единичный интервал длин волн, называется спектральной плотностью излучения. Результаты экспериментов по измерению спектральной плотности излучения абсолютно чёрных тел представлены на рис.4. Таким образом, в обычных условиях излучение в радиодиапазоне (большие значения длин волн λ) и в рентгеновском диапазоне (малые значения длин волн) практически отсутствует. Положение максимума спектральной плотности излучения зависит от температуры тела. На рис.4 показаны в масштабе кривые зависимости спектральной плотности для различных температур.

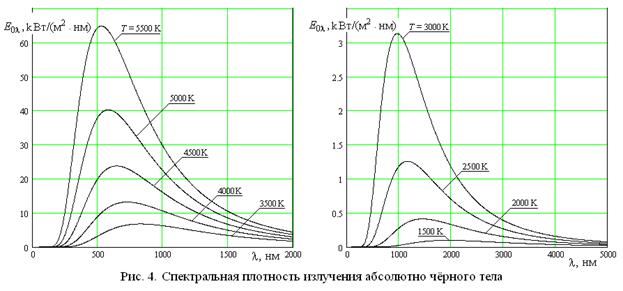
Многие физики второй половины XIX века пытались получить теоретически вид кривой спектральной плотности излучения твёрдых тел используя теорию электромагнетизма Дж.К. Максвелла, однако это им не удалось. Эта теория сравнительно неплохо описывала излучение либо при малых длинах волн, либо при больших, но в любом случае эта теория приводила к физически абсурдному результату: полная энергия электромагнитного излучения любого твёрдого тела должна была быть бесконечно большой. Эта ситуация в физике получила название "ультрафиолетовой катастрофы". В октябре 1900 года немецкий физик Макс Планк (1858 – 1947) "угадал" аналитический вид спектра излучения АЧТ, изображённый на рис.4. Эта формула оказалась следующей:

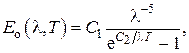
где C₁=3.74·10^-16 Вт·м²; C₂=1.44·10^-2 м·К.

Однако угадывание формулы, описывающей с хорошей точностью изображённую на графике кривую, говорит только о блестящей математической интуиции М. Планка. В этом нет физики. М. Планк, будучи физиком, задался целью обосновать теоретически эту формулу с помощью электромагнитной теории Максвелла, но это ему также не удалось. Тогда, по его словам, он решился на "акт отчаяния". Он предположил абсурдный с точки зрения классической электродинамики механизм излучения в виде конечных порций (по-немецки "квантов") энергии, пропорциональных частоте электромагнитных волн

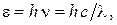
где h – некоторая константа.

Применив к излучению методы теории вероятностей, он получил теоретически формулу, описывающую спектральную плотность излучения твёрдых тел в виде

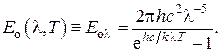
Из сравнения с М. Планк получил значение постоянной

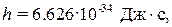
которая в его честь была названа постоянной Планка.

Свои результаты Макс Планк опубликовал в немецком физическом журнале "Annalen der Physik" 14 декабря 1900 года. Эта дата может по праву считаться днём рождения квантовой механики.

2. Закон смещения Вина

Этот закон связывает положение максимума спектральной плотности излучения АЧТ с абсолютной температурой излучающего тела 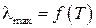. Полученный сначала в результате обработки экспериментальных энергетических спектров, после опубликования М. Планком своей знаменитой формулы этот закон может быть выведен теоретически с помощью простой математической операции поиска экстремума гладкой функции

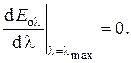
Вычисление производной приводит к трансцендентному алгебраическому уравнению

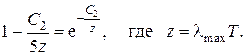
Численное решение даёт 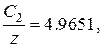откуда с учётом значения С₂ получаем закон смещения Вина

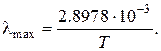
Закон смещения Вина позволяет вычислить температуру излучающего АЧТ по положению максимума в его спектре. Так находятся, например, температуры поверхности Солнца и удалённых звёзд. В частности для Солнца известно

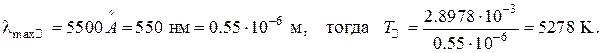
3. Закон Стефана-Больцмана

Этот закон связывает интегральную плотность 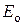излучения АЧТ с его абсолютной температурой. Его также можно получить теоретически, проинтегрировав закон Планка по всем длинам волн. Имеем

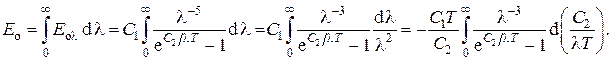
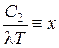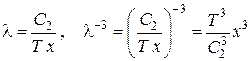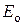Обозначим . Тогда и принимает вид

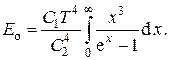
Входящий в это выражение несобственный интеграл оказывается равным 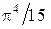. В результате получаем закон Стефана - Больцмана

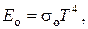
где величина 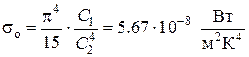носит название постоянной Стефана – Больцмана.

Для практических приложений более удобной является запись закона Стефана – Больцмана в виде

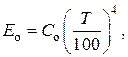
где 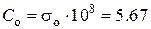(СИ) называется постоянной излучения.

Закон Стефана – Больцмана оказывается справедливым не только для АЧТ, но и для абсолютно серых тел (АСТ), т.е.

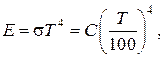
где 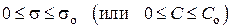и зависит от свойств поверхности излучения, температуры, наличия примесей и т.д.

Отношение

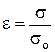
носит название степени черноты поверхности (предполагаемой абсолютно серой), причём 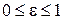. Для АЧТ очевидно .

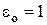4. Закон Кирхгофа

Закон Кирхгофа гласит: для абсолютно серого тела степень черноты численно равна его поглощательной способности, т.е.

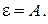
Этот закон является следствием II начала термодинамики и будет получен в дальнейшем как частный случай теории лучистого теплообмена между непрозрачными серыми поверхностями.

5. Закон Ламберта

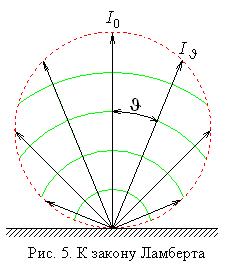Закон Ламберта гласит: интенсивность излучения абсолютно серого тела максимальна в направлении нормали к его поверхности и убывает по закону косинуса угла между направлением нормали и заданным направлением, т.е.

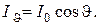
Эта ситуация графически представлена на рис. 5.

По определению интенсивность лучи-стого потока есть поток излучения с единицы площади поверхности, приходящийся на единичный телесный угол.

Примечание. Телесным углом Ω по определению называется отношение площади F участка сферической поверхности к квадрату радиуса r этой сферы, т.е.

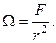
Очевидно, что телесный угол для всей сферы равен 4π (в отличие от плоского угла 2π для окружности).

В соответствии с определением телесного угла интенсивность лучистого потока определяется производной

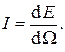
Вычислим плотность лучистого потока E с использованием закона Ламберта, проинтегрировав зависимость по полусфере 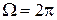. Имеем

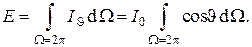
Используя сферические координаты (см. рис. 6), получаем

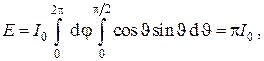
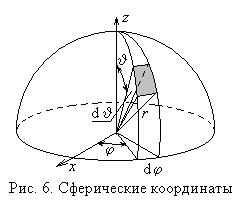т.е. интенсивность излучения в направлении нормали к поверхности составляет долю 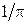, т.е. примерно треть от плотности лучистого потока.

Отметим, что для реальных непрозрачных тел закон Ламберта с достаточной степенью точности справедлив вплоть до угла 60^о от направления нормали, т.е. в пределах телесного угла 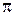, в который излучается 3/4 потока.