Радиационный теплообмен между серыми непрозрачными телами, разделёнными диатермической средой

Диатермической называется среда, не поглощающая и не излучающая электромагнитные волны. Примерами диатермических сред являются вакуум, одно- и двухатомные газы при обычных температурах и давлениях.

Рассмотрим постановку задачи описания теплообмена излучением между телами произвольной формы с произвольным расположением друг относительно друга (см. рис. 1).

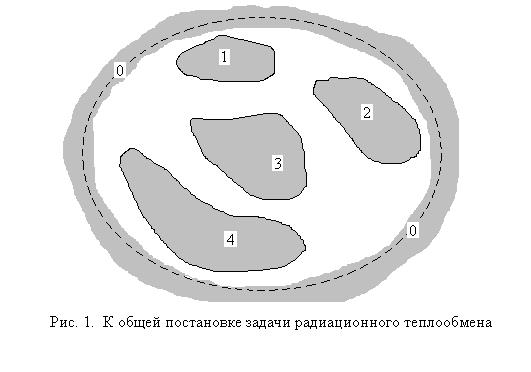
Здесь цифры 1, 2, 3, 4 обозначают тела, цифра 0 обозначает границу полости, в которую заключены рассматриваемые тела. Если такая граница в физическом смысле отсутствует, то её рассматривают в качестве условной, за которой расположена «бесконечная» Вселенная, при этом такая условная граница должна рассматриваться как абсолютно чёрное тело.

При постановке задачи примем следующие допущения.

Задача стационарна, т.е. температуры и оптические свойства поверхностей тел постоянны, геометрические характеристики тел и их взаимное расположение неизменны.

Считаются справедливыми законы геометрической оптики, т.е. пренебрегается дифракционными эффектами, что справедливо при размерах тел, значительно превышающих длины волн излучения (энергия излучения в радиодиапазоне в обычных условиях лучистого теплообмена пренебрежимо мала).

Тела считаются серыми, собственное излучение которых подчиняется закону Стефана-Больцмана.

Собственное излучение с поверхности и отражение падающего излучения подчиняются закону Ламберта, т.е. тела считаются серыми и матовыми.

Дальнейшие допущения будут обсуждены после постановки задачи при перечисленных выше четырёх допущениях.

Таким образом, в общем случае считаются заданными степени черноты 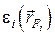, температуры 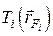, поглощательные и отражательные способности поверхностей тел 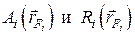. Для описания лучистого теплообмена в системе непрозрачных тел рассмотрим лучистый поток в пределах прямой видимости с элемента поверхности 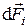тела номер i к элементу 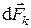поверхности тела номер k (см рис. 2).

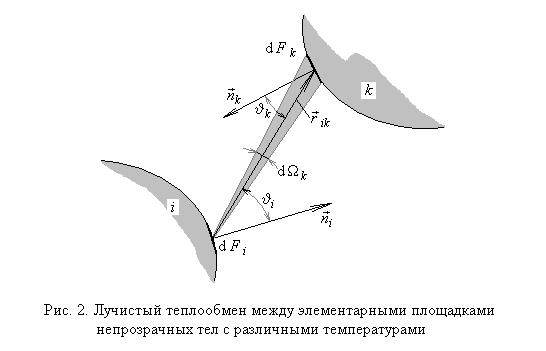
Согласно закону Ламберта интенсивность излучения с единицы площади в окрестности элемента поверхности 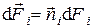в направлении элемента поверхности 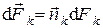составляет

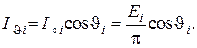
Поток лучистой энергии, приходящийся на единичный телесный угол в направлении 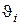с площади 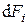будет

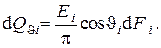
Учтя, что телесный угол, под которым виден элемент поверхности 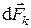из элемента поверхности 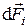есть (см. рис. 2)

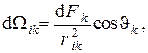
получаем дифференциальное выражение для лучистого потока с элемента поверхности 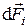тела номер i к элементу 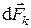поверхности тела номер k в виде

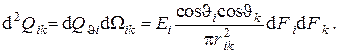
Полный лучистый поток от тела i к телу k определится интегрированием по участкам поверхностей этих тел, находящимся в условиях прямой видимости

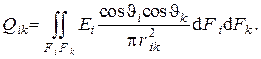
Следует иметь в виду, что каждая из функций в подинтегральном выражении зависит от координат участков поверхностей 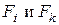, находящихся в условиях прямой видимости, поэтому вычисление этого интеграла представляет существенные трудности. Более того, плотность лучистого потока 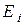здесь в действительности представляет собой суммарный поток собственного и отражённого излучения, о чём речь будет идти в дальнейшем.

Если принять плотность лучистого потока с поверхности 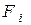на поверхность 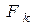постоянной, т.е. если 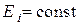, то принимает вид

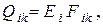
где

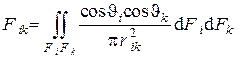
с размерностью м² носит название взаимной поверхности излучения. Эта величина зависит только от взаимного расположения поверхностей и среднего расстояния между ними.

Представим в виде

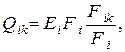
где 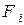есть полная поверхность тела номер i; тогда произведение

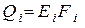
будет представлять поток излучения с поверхности тела i во всех направлениях (а не только в направлении тела номер k ). Отношение

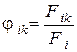
носит название среднего углового коэффициента излучения (или коэффициента облучённости).

Выясним свойства взаимных поверхностей и угловых коэффициентов. Из определения следует симметрия взаимных поверхностей

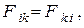
а из определения следует равенство

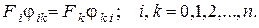
Далее, из – имеем

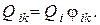
Просуммировав это выражение по всем телам k = 0, 1, 2, …, n, мы должны получить полный лучистый поток от тела номер i, т.е.

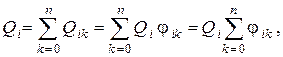
откуда следует

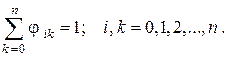
Заметим, что в суммы здесь входят также слагаемые с 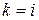, так как для вогнутых тел .

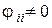Выражения и представляют собой, как легко подсчитать, систему 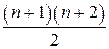линейных алгебраических уравнений для 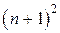неизвестных 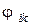. Это обстоятельство позволяет в некоторых случаях избежать вычисления громоздких интегралов , входящих в определение средних угловых коэффициентов . В самом деле, в случае выпуклых или плоских непрозрачных поверхностей, для которых 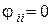, число неизвестных уменьшается с 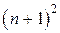до 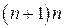. Тогда приравнивая число уравнений и число неизвестных, получаем 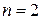, т.е. 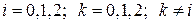. Схема этой задачи представлена на рис. 3.

В этом случае и дают линейную систему из шести уравнений с шестью неизвестными:

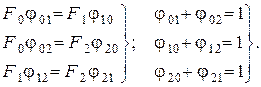
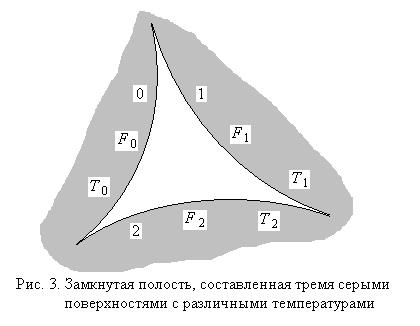
После несложных алгебраических преобразований получаем

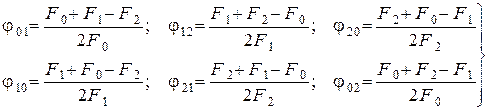
или в сокращённом виде

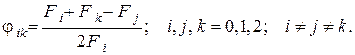
Заметим, что тот же результат будет справедлив и в случае вогнутых изотермических поверхностей с заменой истинных площадей 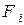площадями 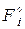плоскостей, «натянутых» на вогнутые поверхности, что иллюстрируется рис. 4.

В общем случае, когда 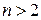, приходится вычислять взаимные поверхности 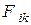и средние угловые коэффициенты 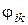. Результаты этих сложных расчётов для различных наиболее важных устройств в высокотемпературной теплообменной технике даются в справочной литературе.

Результирующий лучистый теплообмен между телами с номерами 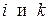будет определяться разностью

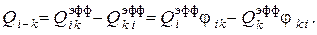
По определению 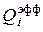представляет собой сумму собственного излучения 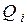и отражённого этим телом падающего на него излучения от всех остальных тел системы включая само себя (если оно вогнуто), т.е.

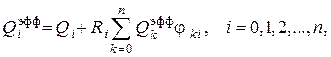
где

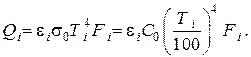
представляет собой систему 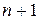линейных алгебраических уравнений с 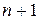неизвестными 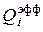. С использованием δ-символа Кронекера эта система уравнений записывается в виде

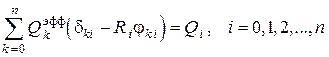
или в развёрнутом виде

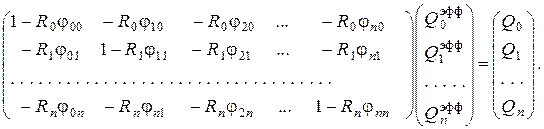
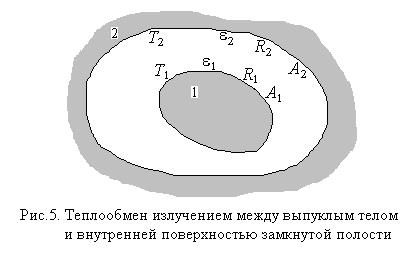
В качестве примера применения вышеизложенного формализма рассмотрим лучистый теплообмен между выпуклым серым непрозрачным телом и внутренней поверхностью окружающей его замкнутой полости (рис. 5).

В этом случае система уравнений и принимает вид

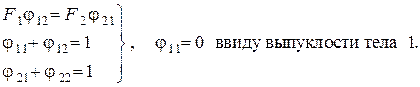
Решение этой системы есть

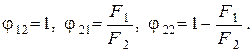
Матричное уравнение приводится тогда к виду

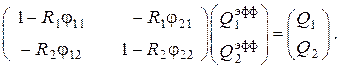
С учётом 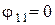получаем

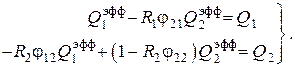
Решая эту систему, находим

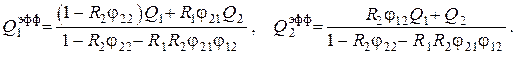
Лучистый поток между телами 1 и 2 определится разностью , что даёт

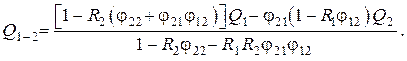
С учётом и получаем окончательно

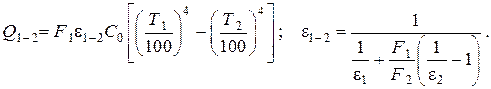
Легко видеть, что при 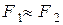этот результат совпадает с ранее полученным для теплообмена излучением между двумя серыми параллельными бесконечными плоскостями.