Задачи оптимизации, решаемые на графах: задача о максимальном потоке в сети, задача о кратчайшем пути.
Пример практической задачи о максимальном потоке. Пусть имеется сеть трубопроводов, соединяющих пункт 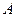 с пунктом
с пунктом 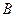 . Трубопроводы могут соединяться и разветвляться в промежуточных пунктах. Количество ресурса, которое может быть перекачено по каждому отрезку трубопровода в единицу времени не безгранично, и определяется диаметром трубы, мощностью насоса и другими параметрами. Вопрос: сколько ресурса можно прокачать через эту сеть трубопровода в единицу времени?
. Трубопроводы могут соединяться и разветвляться в промежуточных пунктах. Количество ресурса, которое может быть перекачено по каждому отрезку трубопровода в единицу времени не безгранично, и определяется диаметром трубы, мощностью насоса и другими параметрами. Вопрос: сколько ресурса можно прокачать через эту сеть трубопровода в единицу времени?
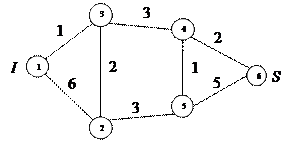
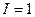 – исток;
– исток; 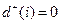 .
.
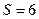 – сток;
– сток; 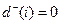 .
.

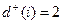 , полустепень исхода
, полустепень исхода
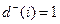 , полустепень захода
, полустепень захода
Пусть 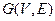 – сеть с двумя особыми вершинами: исток и сток. Дуги сети нагружены неотрицательными вещественными числами и для сети строится матрица пропускных способностей.
– сеть с двумя особыми вершинами: исток и сток. Дуги сети нагружены неотрицательными вещественными числами и для сети строится матрица пропускных способностей.
Множество вещественных чисел будем формулировать следующим образом: 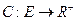 .
.
Числа 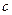 будем называть пропускными способностями дуги. Пропускная способность дуги – максимальное количество ресурса, которое может быть передано по дуге в единицу времени. По дугам сети можно пропустить некоторый поток по пути из истока в сток.
будем называть пропускными способностями дуги. Пропускная способность дуги – максимальное количество ресурса, которое может быть передано по дуге в единицу времени. По дугам сети можно пропустить некоторый поток по пути из истока в сток.
Построим матрицу пропускных способностей транспортной системы:

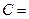
Введем понятие мощности потока по пути и будем обозначать его  . Мощность потока по пути – количество ресурса, пропускаемого по заданному пути в единицу времени. Мощность потока будет определяться выражением
. Мощность потока по пути – количество ресурса, пропускаемого по заданному пути в единицу времени. Мощность потока будет определяться выражением 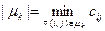 .
.
Будем рассматривать поток из истока в сток.
Рассмотрим поток по пути 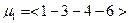 .
. 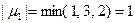 .
.
Рассмотрим поток по пути 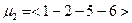 .
. 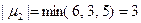 .
.
Дуга, по которой пропущено количество ресурса в единицу времени, совпадающей с пропускной способностью этой дуги называется насыщенной.
Дуги 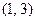 и
и 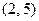 насыщенные.
насыщенные.
Построим матрицу потока по сети:
| -3 | ||||||
| -1 | ||||||
| -1 | ||||||
| -3 | ||||||
| -1 | -3 |
Разобьем множество вершин сети на два непересекающихся подмножества. Чтобы множество вершин сети 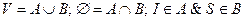 . В этом случае говорят, что на сети произведен разрез, отделяющий исток от стока. Разрез – это совокупность ребер.
. В этом случае говорят, что на сети произведен разрез, отделяющий исток от стока. Разрез – это совокупность ребер. 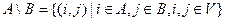 .
.
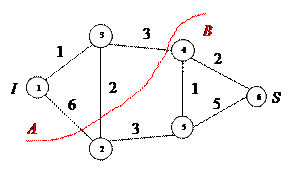
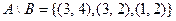 .
.
Для разреза вводят понятие пропускной способности. Пропускная способность разреза 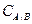 – сумма пропускных способностей ребер этого разреза.
– сумма пропускных способностей ребер этого разреза. 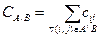 .
.
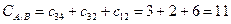 .
.
Теорема Форда-Фалкерсона. На любой сети максимальная величина потока из источника 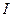 в сток
в сток 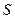 равна минимальной пропускной способности разреза, отделяющего источник от стока.
равна минимальной пропускной способности разреза, отделяющего источник от стока.
Алгоритм нахождения максимального потока:
1. Построить некоторый начальный поток по сети 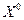 .
.
2. Организовать процедуру построения подмножества 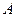 вершин, достижимых из источника
вершин, достижимых из источника 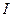 по ненасыщенным ребрам. Если в этом процессе сток
по ненасыщенным ребрам. Если в этом процессе сток 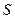 не попадет в подмножество
не попадет в подмножество 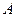 вершин, то построенный поток максимален и задача решена. Если
вершин, то построенный поток максимален и задача решена. Если 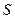 попадает в подмножество
попадает в подмножество 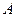 , то перейти к шагу 3.
, то перейти к шагу 3.
3. Выделить путь из источника 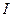 в сток
в сток 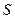 по ненасыщенным ребрам и увеличить поток
по ненасыщенным ребрам и увеличить поток 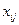 на величину
на величину 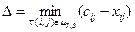 . Тем самым будет построен новый поток по сети. Перейти к шагу 2.
. Тем самым будет построен новый поток по сети. Перейти к шагу 2.
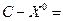
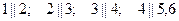
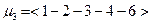 ,
, 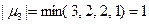 .
.
| -1 | ||||||
| -1 | ||||||
| -1 | ||||||
| -1 |

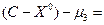
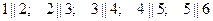
 ,
, 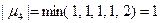 .
.
| -1 | ||||||
| -1 | ||||||
| -1 | ||||||
| -1 | ||||||
| -1 |
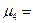
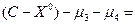
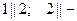
Строим разрез  ,
, 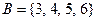 .
.  .
. 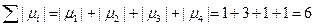 .
.

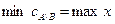 . Т.о. по теореме Форда-Фалкерсона получено: максимальный поток равен 6.
. Т.о. по теореме Форда-Фалкерсона получено: максимальный поток равен 6.
Другой задачей оптимизации на графе является задача нахождения кратчайшего пути в графе. Известно несколько алгоритмов:
1. Флойда – находит кратчайшие пути между всеми парами вершин в орграфе. В этом алгоритме для хранения информации о путях используется матрица 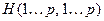 , где
, где 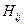 равен
равен 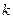 , если
, если 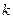 – первая вершина, достигаемая на кратчайшем пути из
– первая вершина, достигаемая на кратчайшем пути из  в
в 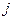 , и равен нулю – если из
, и равен нулю – если из  вершины в
вершины в 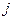 нет вершин.
нет вершин.
2. Дейкстры.
| <== предыдущая лекция | | | следующая лекция ==> |
| Маршруты. Цепи. Циклы. | | | Ориентированные деревья. |
Дата добавления: 2015-12-16; просмотров: 1751;
