Понятие выводимости в логике предикатов.
Исчисление предикатов называют еще теорией первого порядка. В теориях первого порядка не допускается навешивание кванторов по предикатам или по функциям, и не используются предикаты, имеющие в качестве значений своих аргументов другие предикаты. Такие конструкции рассматриваются в теориях предикатов более высоких порядков.
В исчислении предикатов, как и в исчислении высказываний, на первом по важности месте стоит проблема разрешимости. Но в исчислении высказываний проблема разрешимости состояла в решении вопроса: является ли данная сложная функция тождественно истинной, выполнимой или противоречивой?
В исчислении предикатов вопрос следует поставить иначе. Принимает ли данная функция значение «единица»:
- при любых предметных переменных и любых предикатах;
- на некотором множестве предметных переменных и любых предикатах;
- при некоторых значениях предметных переменных и при некоторых предикатах?
- является ли она тождественно ложной, т. е. невыполнимой?
Т.о., в логике предикатов, в отличие от логики высказываний, нет эффективного способа для распознавания общезначимости функций. Поэтому в исчислении предикатов указывается некоторая совокупность формул, которые называются аксиомами и составляют аксиоматическую теорию, и указывается конечное множество отношений между формулами, составляющее правила вывода. Аксиоматическая теория и правила вывода и составляют исчисления предикатов.
Символами исчисления предикатов или алфавитом исчисления предикатов являются символы предметных переменных, символы предикатов, логические символы (отрицание и импликация), символы кванторов, а также скобки и запятая.
Сформулируем аксиомы исчисления предикатов и правила вывода исчисления предикатов.
Аксиомы исчисления предикатов:
Пусть 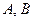 и
и 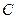 – любые формулы.
– любые формулы.
Аксиома 1.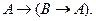
Аксиома 2. 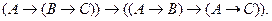
Аксиома 3. 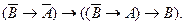
Аксиома 4. 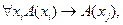 где формула
где формула 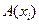 не содержит переменной
не содержит переменной 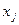 .
.
Аксиома 5.  , где формула
, где формула 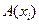 не содержит переменной
не содержит переменной 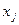 .
.
Правила вывода исчисления предикатов:
1. Пусть 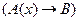 и
и 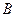 не содержит переменной
не содержит переменной 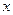 , тогда
, тогда
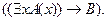
Это правило связывания квантором существования.
2. Пусть 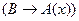 и
и 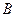 не содержит переменной
не содержит переменной 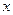 , тогда
, тогда
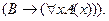
Это правило связывания квантором общности.
3. Связанную переменную формулы 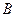 можно заменить другой переменной, не являющейся свободной в
можно заменить другой переменной, не являющейся свободной в 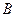 . Это правило переименования связанной переменной.
. Это правило переименования связанной переменной.
Во всякой теории первого порядка правилами вывода являются:
1. Правило Modus Ponens (правило заключения, MP), согласно которому из формул 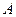 и
и 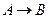 выводится формула
выводится формула 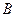 :
: 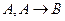 ╞
╞ 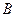 .
.
2. Правило обобщения (связывание квантором общности, GEN), согласно которому из формулы 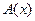 выводится формула
выводится формула 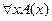 :
: 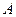 ╞
╞ 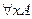 .
.
Для каждой конкретной предметной области могут быть сформулированы собственные аксиомы. Теория 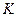 , не содержащая собственных аксиом, называется исчислением предикатов первого порядка. Моделью теории первого порядка называется всякая интерпретация, в которой истины все аксиомы теории
, не содержащая собственных аксиом, называется исчислением предикатов первого порядка. Моделью теории первого порядка называется всякая интерпретация, в которой истины все аксиомы теории 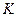 . Если правило вывода MP и GEN применяются к истинным данной интерпретации формулам, то результатом являются формулы, также истинные в той же интерпретации. Следовательно, теория
. Если правило вывода MP и GEN применяются к истинным данной интерпретации формулам, то результатом являются формулы, также истинные в той же интерпретации. Следовательно, теория 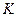 истинна во всякой её модели. Множество формул выводимых по правилам вывода из аксиом теории
истинна во всякой её модели. Множество формул выводимых по правилам вывода из аксиом теории 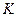 , являются теоремами теории
, являются теоремами теории 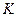 .
.
Кроме теории 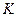 существуют и другие теории. Например, аксиомы
существуют и другие теории. Например, аксиомы 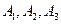 и правило MP определены в теории
и правило MP определены в теории 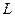 . Следовательно, все теоремы теории
. Следовательно, все теоремы теории 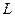 включают множество теорем теории
включают множество теорем теории 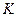 .
.
Говорят, что формула 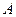 равносильна (логически эквивалентна) формуле
равносильна (логически эквивалентна) формуле 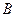 , если каждая из них логически влечет другую:
, если каждая из них логически влечет другую:
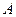 ╞
╞ 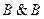 ╞
╞ 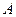
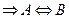 .
.
Из определения следуют следующие утверждения:
1. 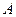 ╞
╞ 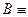 ╞
╞ 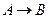 ;
;
2. 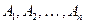 ╞
╞ 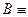 ╞
╞ 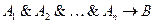 ;
;
3.  ╞
╞ 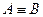 ;
;
4. 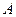 ╞
╞  в некоторой интерпретации;
в некоторой интерпретации;
5. 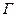 ╞
╞ 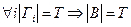 .
.
Аксиомы:
1. 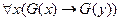 , т.е. если предикат
, т.е. если предикат 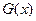 принимает значение истина
принимает значение истина 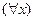 , то он истинен и для
, то он истинен и для  .
.
2. 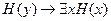 , т.е. если предикат
, т.е. если предикат 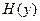 принимает значение истина для какого-нибудь
принимает значение истина для какого-нибудь 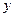 , то существует такой
, то существует такой 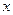 , что
, что 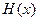 – истина.
– истина.
Пример:
Проверить логическое следование в логике предикатов первого порядка.
Некоторые студенты любят своих преподавателей. Никто не любит невежественных людей. Следовательно, ни один преподаватель не является невежественным.
Все предикаты заданы на области 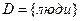 .
.
Пусть
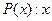 – студент;
– студент;
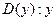 – преподаватель;
– преподаватель;
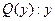 – невежественный;
– невежественный;
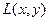 –
– 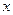 любит
любит 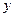 .
.
Формализуем посылки:
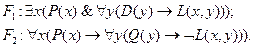
Следствие:
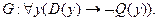
Для доказательства логического следования можно использовать метод от противного.
Предположим, что при истинности посылок 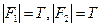 заключение принимает ложное значение:
заключение принимает ложное значение: 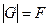 .
.
Из 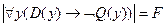 следует, что существует такое
следует, что существует такое 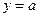 , что
, что 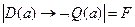 . Тогда
. Тогда 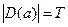 ,
, 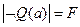 , т.е.
, т.е. 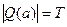 .
.
Из 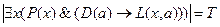 следует, что существует такое
следует, что существует такое 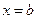 , что
, что 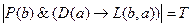 . Тогда
. Тогда 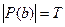 и
и 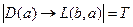 , а т.к.
, а т.к. 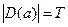 , то
, то 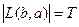 .
.
Посылка  :
:  для всех
для всех 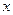 , в том числе для
, в том числе для 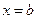 , следовательно,
, следовательно, 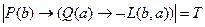 , а т.к.
, а т.к. 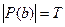 ,
, 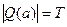 , то из
, то из  следует
следует 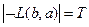 .
.
Т.о., получаем, что истинны оба утверждения: 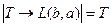 и
и 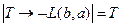 , т.е.
, т.е. 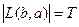 и
и 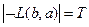 .
.
Полученное противоречие доказывает логическое следование.
| <== предыдущая лекция | | | следующая лекция ==> |
| Правила вынесения кванторов и сколемизация. | | | Правила логического вывода. Вывод на основе принципа резолюций. |
Дата добавления: 2015-12-16; просмотров: 2547;
