Правила логического вывода. Вывод на основе принципа резолюций.
Автоматическое доказательство теорем – краеугольный камень логического программирования, искусственного интеллекта и других современных направлений в программировании.
Постановка задачи.
Алгоритм, который проверяет отношение 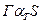 для формулы
для формулы 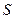 , множества формул
, множества формул 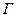 и теории
и теории 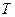 , называется алгоритмом автоматического доказательства теорем. В общем случае такой алгоритм невозможен, т.е. не существует алгоритма, который для любых
, называется алгоритмом автоматического доказательства теорем. В общем случае такой алгоритм невозможен, т.е. не существует алгоритма, который для любых 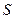 ,
, 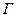 и
и 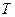 выдавал бы ответ «Да», если
выдавал бы ответ «Да», если 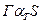 ,и ответ «Нет», если неверно, что
,и ответ «Нет», если неверно, что 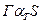 . Более того, известно, что нельзя построить алгоритм автоматического доказательства теорем даже для большинства конкретных достаточно сложных формальных теорий
. Более того, известно, что нельзя построить алгоритм автоматического доказательства теорем даже для большинства конкретных достаточно сложных формальных теорий 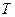 . В некоторых случаях удается построить алгоритм автоматического доказательства теорем, который применим не ко всем формулам теории (то есть частичный алгоритм).
. В некоторых случаях удается построить алгоритм автоматического доказательства теорем, который применим не ко всем формулам теории (то есть частичный алгоритм).
Для некоторых простых формальных теорий (например, исчисление высказываний) и некоторых простых классов формул (например, прикладное исчисление предикатов с одним одноместным предикатом) алгоритмы автоматического доказательства теорем известны.
Поскольку для исчисления высказываний известно, что теоремами являются общезначимые формулы, можно воспользоваться простым методом проверки общезначимости формулы с помощью таблиц истинности, а именно достаточно вычислить истинностное значение формулы при всех возможных интерпретациях (их конечное число). Если во всех случаях получится значение И, то проверяемая формула – тавтология, и, следовательно, является теоремой теории 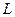 .
.
Наиболее известный классический алгоритм автоматического доказательства теорем называется методом резолюций. Для любого прикладного исчисления предикатов первого порядка 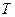 , любой формулы
, любой формулы 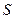 и множества формул
и множества формул 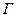 теории
теории 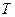 метод резолюций выдает ответ «Да», если
метод резолюций выдает ответ «Да», если 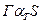 , и выдает ответ «Нет» или не выдает никакого ответа (т.е. «зацикливается»), если неверно, что
, и выдает ответ «Нет» или не выдает никакого ответа (т.е. «зацикливается»), если неверно, что 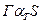 .
.
В основе метода резолюций лежит идея «доказательства от противного».
Метод резолюций в логике высказываний.
Очевидно, что формула 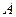 является общезначимой тогда и только тогда, т. е.
является общезначимой тогда и только тогда, т. е. 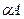 , когда является противоречием формула
, когда является противоречием формула 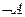 .
.
Формулу 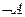 приводим к конъюнктивной нормальной форме (КНФ). КНФ – это формула, равносильная данной формуле и записанная в виде конъюнкции элементарных дизъюнкций, построенных на пропозициональных переменных, т. е. в данном случае
приводим к конъюнктивной нормальной форме (КНФ). КНФ – это формула, равносильная данной формуле и записанная в виде конъюнкции элементарных дизъюнкций, построенных на пропозициональных переменных, т. е. в данном случае
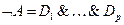 ,
,
где 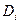 есть дизъюнкция конечного числа пропозициональных переменных или их отрицаний. Тем самым мы формируем множество дизъюнктов
есть дизъюнкция конечного числа пропозициональных переменных или их отрицаний. Тем самым мы формируем множество дизъюнктов 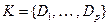 .
.
Два дизъюнкта этого множества 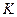
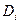 и
и 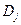 ,содержащие пропозициональные переменные с противоположными знаками, – контрарные литералы, т. е., например,
,содержащие пропозициональные переменные с противоположными знаками, – контрарные литералы, т. е., например, 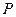 и
и 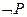 , и, следовательно,
, и, следовательно, 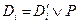 ,
, 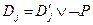 , формируют третий дизъюнкт – резольвенту
, формируют третий дизъюнкт – резольвенту 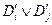 , в которой исключены контрарные литералы:
, в которой исключены контрарные литералы:
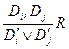 .
.
В частности, если 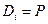 ,
, 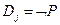 , то резольвента для них – это дизъюнкция, ничего не содержащая (отсутствуют
, то резольвента для них – это дизъюнкция, ничего не содержащая (отсутствуют 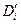 и
и 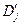 ).Ее называют пустой резольвентой и обозначают знаком □.
).Ее называют пустой резольвентой и обозначают знаком □.
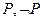
——— 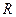 .
.
□
Резольвента 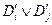 – это логическое следствие дизъюнктов
– это логическое следствие дизъюнктов 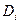 и
и 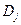 , т. е.
, т. е. 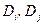 ╞
╞ 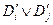 . Неоднократно применяя правило получения резольвент к множеству дизъюнктов, стремятся получить пустой дизъюнкт □. Наличие пустого дизъюнкта □ свидетельствует о получении противоречия, поскольку пустая резольвента получается из двух противоречащих друг другу дизъюнктов
. Неоднократно применяя правило получения резольвент к множеству дизъюнктов, стремятся получить пустой дизъюнкт □. Наличие пустого дизъюнкта □ свидетельствует о получении противоречия, поскольку пустая резольвента получается из двух противоречащих друг другу дизъюнктов 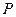 и
и 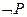 , каждый из которых – логическое следствие формулы
, каждый из которых – логическое следствие формулы 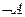 в соответствии с правилом
в соответствии с правилом 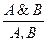 .
.
Получение противоречия с помощью формулы 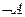 означает общезначимость формулы
означает общезначимость формулы 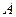 .
.
Алгоритм метода резолюций:
Шаг 1. Принять отрицание формулы 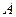 , т. е.
, т. е. 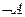 .
.
Шаг 2. Привести формулу 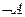 к конъюнктивной нормальной форме.
к конъюнктивной нормальной форме.
Шаг 3. Выписать множество ее дизъюнктов: 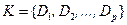 .
.
Шаг 4. Выполнить анализ пар множества 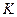 по правилу: если существуют дизъюнкты
по правилу: если существуют дизъюнкты 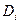 и
и 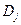 , один из которых (
, один из которых ( 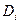 )содержит литерал
)содержит литерал 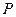 , а другой (
, а другой ( 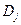 ) – контрарный литерал
) – контрарный литерал 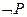 , то нужно соединить эту пару логической связкой дизъюнкции (
, то нужно соединить эту пару логической связкой дизъюнкции ( 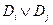 ) и сформировать новый дизъюнкт - резольвенту, исключив контрарные литералы
) и сформировать новый дизъюнкт - резольвенту, исключив контрарные литералы 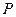 и
и 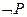 .
.
Шаг 5. Если в результате соединения дизъюнктов, содержащих контрарные литералы, будет получена пустая резольвента □, то результат достигнут (доказательство подтвердило противоречие), в противном случае включить резольвенту в множество дизъюнктов 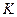 и перейти к шагу 4.
и перейти к шагу 4.
При реализации указанного алгоритма возможны три случая.
1. Среди текущего множества дизъюнктов нет резольвируемых. Это означает, что формула 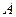 не является общезначимой.
не является общезначимой.
2. На каком-то шаге получается пустая резольвента. Формула 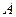 общезначима.
общезначима.
3. Процесс не останавливается, т. е. множество дизъюнкт пополняется все новыми резольвентами, среди которых нет пустых. В таком случае нельзя ничего сказать об общезначимости формулы 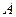 .
.
Метод резолюций в логике предикатов.
Метод резолюций работает с особой стандартной формой формул, которые называются предложениями. Предложение – это бескванторная дизъюнкция литералов. Любая формула исчисления предикатов может быть преобразована в множество предложений.
Если формула 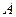 не содержит предикатов и знаков операций (функций), то фактически имеем формулу исчисления высказываний, поскольку предикаты можно рассматривать как пропозициональные переменные. Следовательно, метод резолюций не требует существенных изменений. В случае, если формула
не содержит предикатов и знаков операций (функций), то фактически имеем формулу исчисления высказываний, поскольку предикаты можно рассматривать как пропозициональные переменные. Следовательно, метод резолюций не требует существенных изменений. В случае, если формула 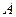 содержит кванторы, то ее надо привести к предваренной форме, а затем устранить кванторы, вводя сколемовские функции. При этом появятся знаки операций (функций). Затем полученную формулу приводят к конъюнктивной нормальной форме и ищут резольвенты для дизъюнктов, которые в данном случае именуют предложениями.
содержит кванторы, то ее надо привести к предваренной форме, а затем устранить кванторы, вводя сколемовские функции. При этом появятся знаки операций (функций). Затем полученную формулу приводят к конъюнктивной нормальной форме и ищут резольвенты для дизъюнктов, которые в данном случае именуют предложениями.
Для применения правила резолюции нужны контрарные литералы в резольвируемых предложениях. Пусть 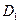 и
и 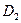 – два предложения в исчислении предикатов. Правило вывода
– два предложения в исчислении предикатов. Правило вывода
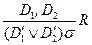
называется правилом резолюции в исчислении предикатов, если в предложениях 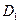 и
и 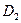 существуют унифицируемые контрарные литералы
существуют унифицируемые контрарные литералы 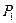 и
и 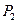 , т.е.
, т.е. 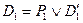 и
и 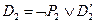 , причем атомарные формулы
, причем атомарные формулы 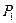 и
и 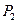 являются унифицируемыми наиболее общим унификатором
являются унифицируемыми наиболее общим унификатором 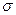 . В этом случае резольвентой предложений
. В этом случае резольвентой предложений 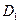 и
и 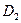 является предложение
является предложение 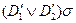 , полученное из предложения
, полученное из предложения 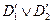 применением унификатора
применением унификатора 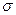 .
.
Пусть два контрарных литерала, в данном случае 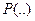 и
и 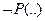 , содержат два разных терма. Например,
, содержат два разных терма. Например, 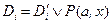 и
и 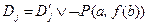 . В этом случае проводят их унификацию, т. е. замену термов (символическая запись
. В этом случае проводят их унификацию, т. е. замену термов (символическая запись 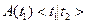 означает замену в формуле
означает замену в формуле 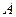 терма
терма 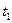 на терм
на терм 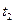 ):
):
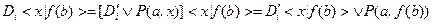 ,
,
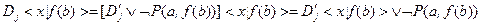 .
.
Далее находят резольвенту
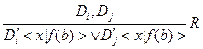 .
.
Сформулируем более строго правила замены термов и понятие унификации.
Замена – это пара вида 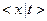 , где
, где 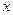 – переменная, а
– переменная, а 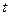 – терм. Применение замены
– терм. Применение замены 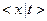 к терму
к терму 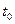 , входящему в некоторую формулу, определяется индуктивно:
, входящему в некоторую формулу, определяется индуктивно:
1) 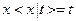 , если
, если 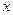 – переменная;
– переменная;
2) 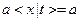 , если
, если 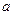 – константа;
– константа;
3) 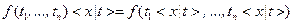 .
.
Т.о., унификация двух последовательных термов 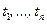 и
и 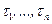 – это замена
– это замена 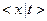 такая, что
такая, что 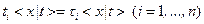 .
.
Резольвенту для дизъюнктов 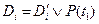 и
и 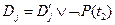 находят с помощью унификации термов
находят с помощью унификации термов 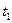 и
и 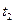 :
:
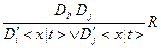 .
.
Пример: Имеется два дизъюнкта:
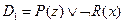 ,
, 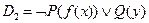 .
.
Заменим
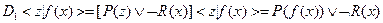 ,
,
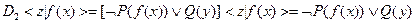 .
.
Тогда резольвента для 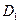 и
и 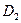 есть дизъюнкт
есть дизъюнкт 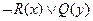 .
.
Пример:Для дизъюнктов 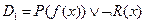 ,
, 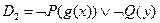 нет унификации.
нет унификации.
Пример: Некоторые студенты любят своих преподавателей. Никто не любит невежественных людей. Следовательно, ни один преподаватель не является невежественным.
Все предикаты заданы на области 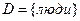 .
.
Пусть
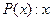 – студент;
– студент;
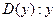 – преподаватель;
– преподаватель;
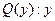 – невежественный;
– невежественный;
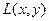 –
– 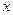 любит
любит 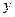 .
.
Формализуем посылки:
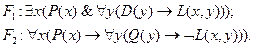
Следствие:
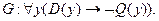
Для доказательства логического следования можно использовать метод резолюций.
Найдем предваренные нормальные формы (ПНФ) для посылок.
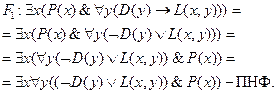
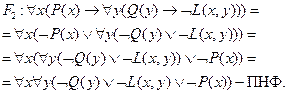
Найдем сколемовскую стандартную форму (ССФ) посылок.
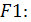 Элиминируем квантор
Элиминируем квантор 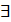 в формуле
в формуле 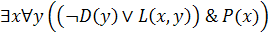 . Положим
. Положим 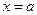 , получим ССФ посылки
, получим ССФ посылки 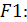 :
:
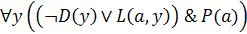 .
.
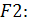
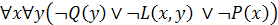 находится в сколемовской стандартной форме.
находится в сколемовской стандартной форме.
Возьмем отрицание от следствия 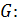 :
:
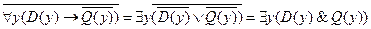 .
. 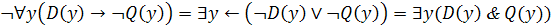
Это ПНФ. Элиминируем квантор 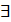 , положив
, положив 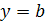 :
:
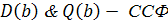
Получим множество дизъюнктов:
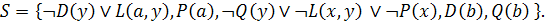 .
.
Построим резолютивный вывод:
1) 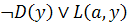 ;
;
2) 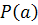 ;
;
3) 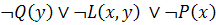 ;
;
4) 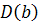 ;
;
5) 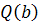 ;
;
6) 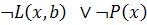
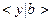
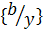 , резольвента 5, 3;
, резольвента 5, 3;
7) 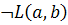
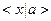
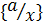 , резольвента 2, 6;
, резольвента 2, 6;
8) 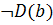
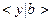
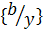 , резольвента 1, 7;
, резольвента 1, 7;
9)  □ резольвента 4, 8.
□ резольвента 4, 8.
| <== предыдущая лекция | | | следующая лекция ==> |
| Понятие выводимости в логике предикатов. | | | Способы задания графов. |
Дата добавления: 2015-12-16; просмотров: 2853;
