Способы задания графов.
Основные понятия и определения теории графов. Способы задания графов. Эйлеровы графы. Деревья. Сети.
Основные задачи, которые привели к созданию теории графов:

| Задача о Кенингсберских мостах. Обойти все четыре части суши, пройдя по каждому мосту один раз и вернуться в исходную точку. |

| Задача о трех домах и трех колодцах. Имеется три дома и три колодца. Провести от каждого дома по тропинке так, чтобы они не пересекались. |
| Задача о четырех красках. Любую карту на плоскости раскрасить четырьмя красками так, чтобы никакие две соседние области не были закрашены одним цветом. |
Графом 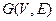 называется совокупность двух множеств: непустого множества вершин
называется совокупность двух множеств: непустого множества вершин 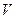 и множества
и множества 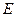 неупорядоченных пар различных элементов множества
неупорядоченных пар различных элементов множества 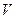 . Множество
. Множество 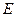 называется множеством ребер
называется множеством ребер 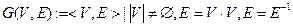 .
.
Число вершин графа 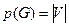 .
.
Число ребер графа 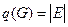 .
.
Пусть 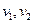 – вершины графа
– вершины графа 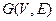 с множеством вершин
с множеством вершин 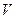 . Тогда
. Тогда 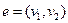 – ребро, соединяющее эти вершины. Вершина
– ребро, соединяющее эти вершины. Вершина 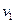 и ребро
и ребро 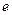 инцидентны, вершина
инцидентны, вершина 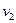 и ребро
и ребро 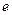 также инцидентны.
также инцидентны.
Две вершины называются смежными, если они соединены ребром (дугой). Смежные вершины – две вершины, инцидентные одному ребру.
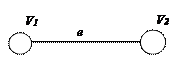
Два ребра называются смежными, если они соединены вершиной (узлом).Смежные ребра – два ребра, инцидентные одной вершине.

Множество вершин, смежных с вершиной 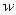 называют множеством смежности вершины
называют множеством смежности вершины 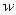 . Обозначают:
. Обозначают: 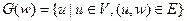 .
.

Способы задания графов.
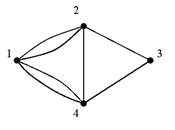
Обычно граф изображают диаграммой в которой вершины представлены окружностями, а ребра – линиями.
Полным является граф, у которого все вершины смежны между собой. 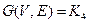 – полный граф с четырьмя вершинами.
– полный граф с четырьмя вершинами.

Если элементами множества 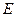 являются упорядоченные пары, то граф называется ориентированным или орграфом. Ребра в таком орграфе называют дугами.
являются упорядоченные пары, то граф называется ориентированным или орграфом. Ребра в таком орграфе называют дугами.

Если элементом множества 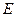 может быть пара одинаковых элементов множества
может быть пара одинаковых элементов множества 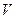 , то такой элемент множества
, то такой элемент множества 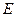 называют петлей. А граф называют – графом с петлями или псевдографом.
называют петлей. А граф называют – графом с петлями или псевдографом.
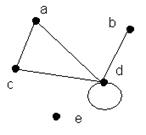
Если  не является множеством, а набором (кортежем), содержащим несколько одинаковых элементов, то эти элементы называют кратными ребрами, а граф – мультиграфом.
не является множеством, а набором (кортежем), содержащим несколько одинаковых элементов, то эти элементы называют кратными ребрами, а граф – мультиграфом.
Если элементами множества 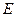 являются необязательно двухэлементные, то такие элементы множества
являются необязательно двухэлементные, то такие элементы множества 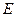 называют гипердугами, а граф – гиперграфом.
называют гипердугами, а граф – гиперграфом.
Если задана функция 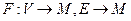 F, то
F, то 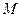 – множество пометок, а граф называется помеченным или нагруженным.
– множество пометок, а граф называется помеченным или нагруженным.
Основной способ задания графа – в виде матрицы смежности вершин. Элемент 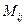 равен 1, если
равен 1, если 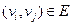 и равен 0, если
и равен 0, если 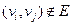 .
.
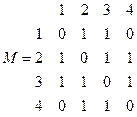
Также графы можно задавать с помощью матрицы инцидентности. Представление графа  с помощью матрицы
с помощью матрицы  , отражающей инцидентность вершин и ребер: для неориентированного графа элемент
, отражающей инцидентность вершин и ребер: для неориентированного графа элемент 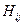 равен 1, если вершина
равен 1, если вершина 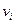 инцидентна ребру
инцидентна ребру 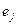 , иначе элемент
, иначе элемент 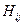 равен 0.
равен 0.
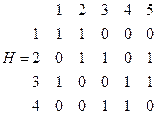
Граф задается также списками смежности. Это списочная структура отражает смежность вершин и состоит из массива указателей на списки смежных вершин.
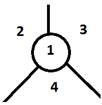
Степень (валентность) вершины 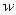 в графе
в графе 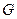 – количество ребер, инцидентных вершине
– количество ребер, инцидентных вершине 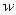 . Обозначают
. Обозначают 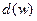 .
.
Для любой 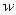 :
: 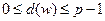 .
.
Минимальная степень вершины графа 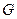 обозначается
обозначается 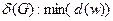 .
.
Максимальная степень вершины графа 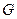 обозначается
обозначается 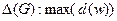 .
.
Если степени всех вершин равны 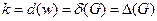 , то граф называется регулярным.
, то граф называется регулярным. 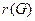 – степень регулярности графа. Для нерегулярных графов
– степень регулярности графа. Для нерегулярных графов 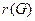 не определена.
не определена.
Для орграфа число дуг, исходящих из вершины 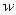 , называют полустепенью исхода и обозначают
, называют полустепенью исхода и обозначают 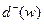 , а число дуг, входящих в вершину
, а число дуг, входящих в вершину 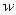 , называют полустепенью захода и обозначают
, называют полустепенью захода и обозначают 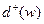 .
.
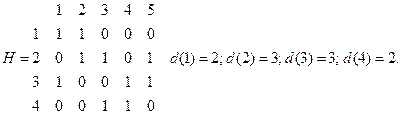
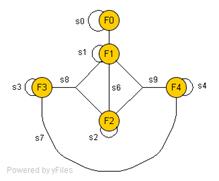
Определим полустепени захода и полустепени исхода всех вершин графа:

d-(1)=2; d-(2)=2; d-(3)=1; d-(4)=0;
d+(1)=0; d+(2)=1; d+(3)=1; d+(4)=3.
Ориентированный граф, имеющий две вершины: в одной (сток), у которой полустепень захода равна нулю, а в другой (исток), у которой полустепень исхода равна нулю называют сетью.
Теорема Эйлера. Сумма степеней вершин графа равна удвоенному количеству ребер.
Теорема справедлива как для неориентированных графов, так и для ориентированных графов.
Для неориентированных графов: 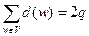 .
.
Для ориентированных графов: 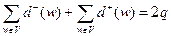 .
.
Дата добавления: 2015-12-16; просмотров: 2017;
