Правила вынесения кванторов и сколемизация.

Определение 14.1. Формулы, в которых из логических символов имеются только символы конъюнкции, дизъюнкции и отрицания, причем символ отрицания встречается над символами предикатов, будем называть приведенными.

Пример:

формула 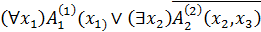– приведенная, формула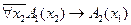 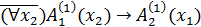– неприведенная.

Определение 14.2. Для любой формулы существует равносильная ей приведенная формула, причем множества свободных и связанных переменных этих формул совпадают. Такая приведенная формула называется приведенной формой данной формулы.

Определение 14.3. Приведенная формула называется нормальной,если она не содержит символов кванторов или все символы кванторов стоят впереди, т.е. логические символы и символы предикатов стоят в области действия каждого квантора.

Определение 14.4. Для любой приведенной формулы существует равносильная ей нормальная формула той же длины (под длиной формулы будем понимать общее число входящих в нее символов предикатов, логических символов и символов кванторов). Нормальная формула называется нормальной формой данной формулы.

Пример:

формула в приведенной нормальной форме: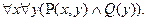

Алгоритм преобразования формул в приведенную нормальную форму:

1. исключить логические связки и с помощью следующих равносильностей:

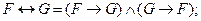
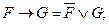
2. протаскивание отрицаний:

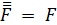
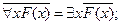
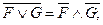
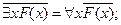
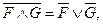
после этого этапа знак 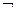находится внутри формулы;

3. разделение связанных переменных:

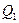, где и 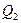– любые кванторы;

после этого этапа формула не содержит случайных совпадающих связанных переменных;

4. использование равносильных формул для вынесения кванторов в начало формулы

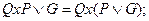
, где 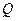– любой квантор;

после этого этапа формула находится в приведенной нормальной форме.

Пример:

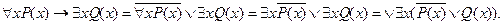
Определение 14.5. Формула 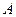находится в предваренной нормальной форме (ПНФ), если она имеет вид: 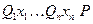, где каждое 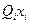есть либо 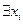, либо 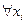, a 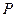– формула в конъюнктивной нормальной форме, не содержащая кванторов.

Определение 14.6. Предваренная нормальная форма (ПНФ), содержащая только кванторы всеобщности, называется сколемовской нормальной формой (СНФ).

Процедура приведения ПНФ к сколемовской форме заключается в элиминации (удалении) кванторов существования.

Пусть формула 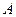находится в предваренной нормальной форм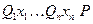е , где 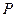– конъюнктивная нормальная форма. Если квантор существования – первый слева квантор в 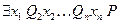, то его можно элиминировать следующим образом. Выберем константу 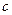, отличную от других констант, входящих в 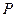, заменим все вхождения 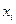, встречающиеся в 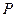, на 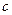и вычеркнем квантор :

.

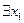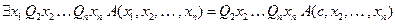Если же перед квантором существования стоит квантор всеобщности, например, 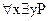, то переменная 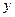попадает в область действия квантора всеобщности и выражение 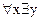означает наличие некоторой функциональной зависимости 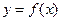. Если квантору существования предшествует несколько кванторов всеобщности, то функция зависит от всех переменных, по которым навешены эти кванторы:

.

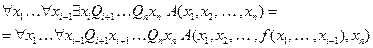Последняя формула и есть сколемовская нормальная форма (СНФ). Иногда ее для краткости именуют стандартной формой формулы 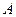. Функции, используемые для замены переменных квантора существования, называются сколемовскими функциями (константы есть нуль-местные функции).

Пример: провести сколемизацию формулы

.

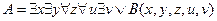Переменные 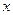и 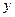заменяем на константы 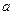и 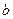соответственно. Переменные 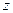и 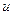оставляем, а вместо 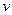вводим сколемовскую функцию 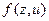. Получаем формулы

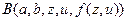и .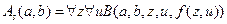

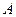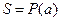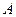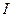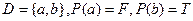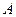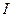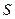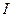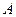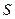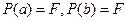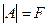Если предваренная нормальная форма эквивалентна исходной формуле, то сколемовская нормальная форма формулы , вообще говоря, не эквивалентна ей. Например, пусть и есть стандартная форма формулы . Пусть есть следующая интерпретация: область . Тогда истинна в , но ложна в . Т.о., не эквивалентна . Однако, если , то и 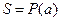также принимает значение для любого 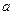. Т.о., 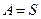в том, и только том случае, если 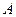противоречива.