Правильно построенные формулы. Тождественные преобразования формул.
Определение 13.1. Формула логики предикатов называется атомарной, т.е. элементарной, если в ней нет связанных переменных.
Пусть  – формула, тогда
– формула, тогда 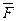 – тоже формула. Свободные и связанные переменные формулы
– тоже формула. Свободные и связанные переменные формулы 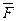 – это соответственно свободные и связанные переменные формулы
– это соответственно свободные и связанные переменные формулы  . Пусть
. Пусть  и
и 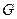 – формулы, причем в них нет предметных переменных, которые были бы связаны в одной формуле и свободны в другой. Тогда
– формулы, причем в них нет предметных переменных, которые были бы связаны в одной формуле и свободны в другой. Тогда 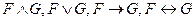 – формулы, в которых свободные переменные формул
– формулы, в которых свободные переменные формул  и
и 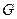 остаются свободными, а связанные – связанными.
остаются свободными, а связанные – связанными.
Пусть  – формула, содержащая свободную переменную
– формула, содержащая свободную переменную 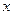 . Тогда
. Тогда 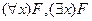 – тоже формулы, в которых переменная
– тоже формулы, в которых переменная 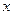 связанная, а остальные свободные переменные, входящие в
связанная, а остальные свободные переменные, входящие в  , остаются свободными.
, остаются свободными.
По определению формулы никакая переменная не может быть одновременно свободной и связанной.
Определение 13.2. Значение формулы определено лишь тогда, когда задана какая-то интерпретация входящих в неё символов. Под интерпретацией понимают систему 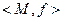 , состоящую из непустого множества
, состоящую из непустого множества 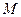 и соответствия
и соответствия 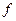 , которое сопоставляет каждой формуле определенный предикат. При заданной интерпретации предметные переменные пробегают множество
, которое сопоставляет каждой формуле определенный предикат. При заданной интерпретации предметные переменные пробегают множество 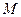 , а логические символы и символы кванторов имеют свой обычный смысл.
, а логические символы и символы кванторов имеют свой обычный смысл.
Пример:
Пусть 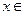 {люди},
{люди}, 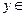 {объекты, которые можно читать и писать}. На этих областях определения заданы предикаты:
{объекты, которые можно читать и писать}. На этих областях определения заданы предикаты: 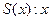 – студент,
– студент, 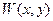 :
: 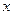 любит читать
любит читать 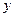 ,
, 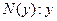 – роман,
– роман, 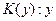 – конспект,
– конспект, 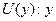 – учебник.
– учебник.
Следующие высказывания запишем в виде формул логики предикатов.
Некоторые учебники представляют собой конспект:
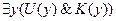 .
.
Ни один роман не является учебником:
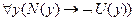 .
.
Каждый читает какие-нибудь учебники:
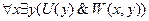 .
.
Некоторые студенты читают только учебники:
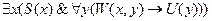 .
.
Пример:
Построить таблицы истинности на области интерпретации 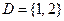 формулы:
формулы:
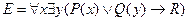
Предикаты 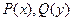 на области интерпретации
на области интерпретации 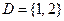 принимают следующие значения:
принимают следующие значения:
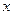
| 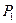
| 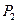
| 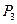
| 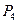
| 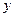
| 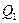
| 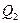
| 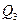
| 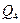
|
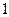
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
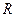 – замкнутая формула, т. е. высказывание, которое принимает значения «истина» (
– замкнутая формула, т. е. высказывание, которое принимает значения «истина» (  ) и «ложь» (
) и «ложь» (  ).
).
Поскольку предикат 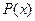 принимает четыре значения, предикат
принимает четыре значения, предикат 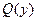 – четыре значения, формула
– четыре значения, формула 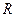 – два значения и в формуле
– два значения и в формуле 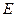 нет свободных переменных, таблица истинности будет состоять из
нет свободных переменных, таблица истинности будет состоять из 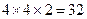 строк. Очевидно, что если интерпретация
строк. Очевидно, что если интерпретация 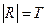 , то
, то 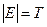 , поэтому остается вычислить значение формулы на оставшихся 16 интерпретациях формулы при
, поэтому остается вычислить значение формулы на оставшихся 16 интерпретациях формулы при 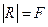 .
.
Пусть 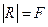 . Рассмотрим вычисление значения формулы на интерпретации
. Рассмотрим вычисление значения формулы на интерпретации 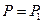 и
и 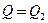 .
.
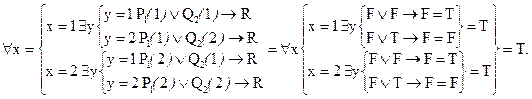
Пусть 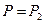 и
и 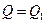 . Тогда
. Тогда
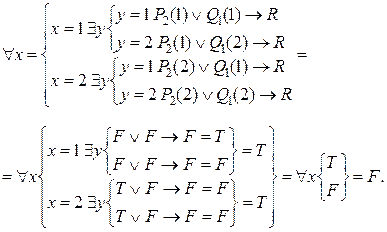
Аналогично находятся остальные значения формулы 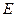 :
:
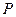
| 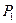
| 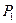
| 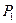
| 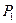
| 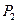
| 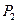
| 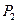
| 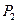
| 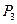
| 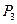
| 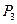
| 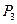
| 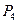
| 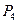
| 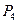
| 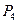
|
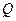
| 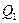
| 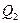
| 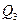
| 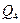
| 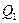
| 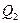
| 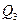
| 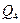
| 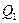
| 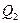
| 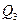
| 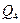
| 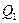
| 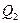
| 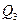
| 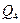
|
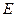
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
Пусть формулы  и
и 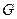 имеют одно и то же множество свободных переменных .
имеют одно и то же множество свободных переменных .
Определение 13.3. Формулы  и
и 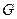 равносильны в данной интерпретации, если они принимают одинаковые значения на любом наборе свободных переменных, т. е. выражают в данной интерпретации один и тот же предикат.
равносильны в данной интерпретации, если они принимают одинаковые значения на любом наборе свободных переменных, т. е. выражают в данной интерпретации один и тот же предикат.
Определение 13.4. Формулы  и
и 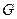 равносильны на множестве
равносильны на множестве 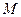 , если они принимают одинаковые значения во всех интерпретациях, заданных на множестве
, если они принимают одинаковые значения во всех интерпретациях, заданных на множестве 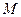 .
.
Определение 13.5. Формулы  и
и 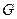 равносильны в логике предикатов, если они равносильны на всех множествах
равносильны в логике предикатов, если они равносильны на всех множествах 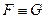 .
.
Рассмотрим правила перехода от одних формул к другим, им равносильным.
1. Перенос квантора через отрицание. Пусть 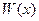 – формула, содержащая свободную переменную
– формула, содержащая свободную переменную 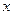 . Тогда справедливы равносильности:
. Тогда справедливы равносильности:
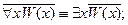
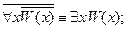
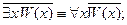
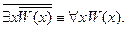
2. Вынос квантора за скобки. Пусть формула 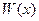 содержит свободную переменную
содержит свободную переменную 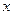 , а формула
, а формула 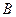 не содержит переменной
не содержит переменной 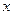 . Формулы
. Формулы 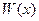 и
и 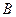 удовлетворяют правилам создания формул. Тогда справедливы равносильности:
удовлетворяют правилам создания формул. Тогда справедливы равносильности:
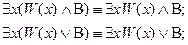
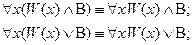
3. Перестановка одноименных кванторов.
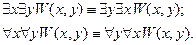
4. Переименование связанных переменных. Заменяя связанную переменную формулы 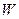 другой переменной, не входящей в эту формулу, в кванторе и всюду в области действия квантора, получим формулу, равносильную
другой переменной, не входящей в эту формулу, в кванторе и всюду в области действия квантора, получим формулу, равносильную 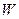 .
.
Рассмотрим обоснование равносильности формул по Готлобу Фреге. Пусть даны две формулы 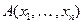 и
и 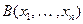 . Формула
. Формула 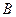 является логическим следствием формулы
является логическим следствием формулы 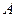 , если во всякой интерпретации формула
, если во всякой интерпретации формула 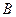 выполнена на каждом наборе переменных
выполнена на каждом наборе переменных 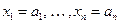 , на котором выполнена формула
, на котором выполнена формула 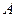 . Обозначение:
. Обозначение: 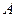 ╞
╞ 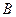 .
.
Теорема: 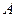 ╞
╞ 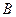
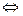
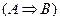 (является тавтологией).
(является тавтологией).
Определение 13.6. Формулы 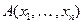 и
и 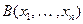 . называются равносильными, если
. называются равносильными, если 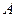 ╞
╞ 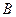 и
и 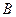 ╞
╞ 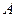 . Для равносильных формул используется следующая запись:
. Для равносильных формул используется следующая запись: 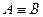 .
.
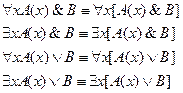
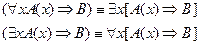
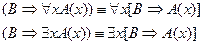
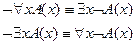
| <== предыдущая лекция | | | следующая лекция ==> |
| Дизъюнктивная нормальная форма. | | | Правила вынесения кванторов и сколемизация. |
Дата добавления: 2015-12-16; просмотров: 2052;
