Дизъюнктивная нормальная форма.

Определение 9.7. Обозначим , если , и , если . Символ называется литералом булевой функции .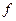

Рассмотрим конъюнкцию . Существует различных наборов значений переменных 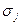. Соответственно имеется различных конъюнкций вида .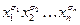

Определение 9.8. Конъюнкция 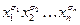равна единице тогда и только тогда, когда для всех и её называют конституентой 1.

Теорема. Любая булева функция может быть представлена в виде дизъюнкции конституент единицы:

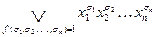, где конституенты записываются для всех таких, что .

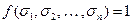Такое представление булевой функции называется совершенной дизъюнктивной нормальной формой (СДНФ).

Пример:

Пусть булева функция задана таблицей истинности. Требуется записать ее в СДНФ.

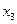
Имеем:

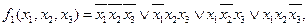
Заметим, что полученная запись функции может быть упрощена следующим образом:

Определение 9.9. Всякую конъюнкцию переменных функции, взятых с отрицанием или без отрицания, называют элементарной. Дизъюнкцию элементарных конъюнкций называют дизъюнктивной нормальной формой (ДНФ).

Так, выше для функции имеем две ДНФ.