Понятие логического базиса. Понятие о полноте системы булевских функций. Полиномы Жегалкина. Дизъюнктивные и конъюнктивные нормальные формы.
Булевы функции из множества функций 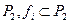 , можно выразить через другие функции. Например:
, можно выразить через другие функции. Например:
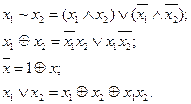
Пусть имеется система булевых функций:
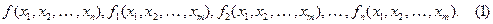
Определение 9.1. Функция 
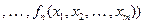 называется суперпозицией функций системы.
называется суперпозицией функций системы.
Определение 9.2. Множество 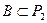 булевых функций называется замкнутым, если в результате суперпозиции функции множества
булевых функций называется замкнутым, если в результате суперпозиции функции множества  могут быть получены только функции, принадлежащие множеству
могут быть получены только функции, принадлежащие множеству  .
.
Определение 9.3. Система булевых функций (1) называется функционально полной в множестве 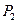 всех булевых функций, если в результате суперпозиции функций этой системы можно получить любую булеву функцию.
всех булевых функций, если в результате суперпозиции функций этой системы можно получить любую булеву функцию.
Функции из множества 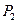 обладают определенными свойствами, в соответствии с которыми выделяют классы булевых функций. Пусть имеется булева функция
обладают определенными свойствами, в соответствии с которыми выделяют классы булевых функций. Пусть имеется булева функция 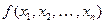 , зависящая от
, зависящая от 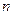 переменных. Пусть переменным этой функции присвоены значения:
переменных. Пусть переменным этой функции присвоены значения: 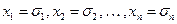 , где
, где  . Тогда
. Тогда 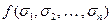 есть значение функции
есть значение функции 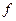 при заданных значениях аргумента.
при заданных значениях аргумента.
Классы булевых функций:
1. Булева функция сохраняет константу 0, если 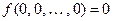 . (Класс K0).
. (Класс K0).
2. Булева функция сохраняет константу 1, если 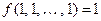 . (Класс K1).
. (Класс K1).
3. Булева функция называется самодвойственной, если она совпадает с двойственной себе функцией, т.е. имеет место равенство 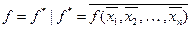 . (Класс S).
. (Класс S).
4. Булева функция называется линейной, если она может быть записана в виде: 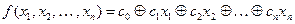 , где
, где 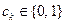 . (Класс L).
. (Класс L).
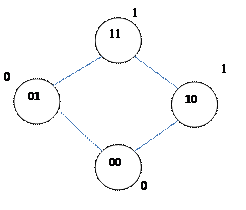
5. Булева функция называется монотонной, если для любых двух наборов, таких что 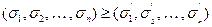 имеет место неравенство:
имеет место неравенство: 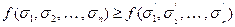 . (Класс M).
. (Класс M).
Будем говорить, что набор значений переменных  не меньше набора
не меньше набора 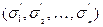 , если
, если  . Тогда
. Тогда 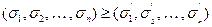 . В противном случае функции несравнимы.
. В противном случае функции несравнимы.
Теорема: каждый из классов булевых функций (K0, K1, S, L, M) и множество всех булевых функций, является замкнутым.
Доказательство замкнутости всех булевых функций: в самом деле, каждая из функций определена и принимает свои значения из множества 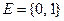 , откуда следует, что при суперпозиции вместо переменных некоторой булевой функции могут быть взяты булевы функции. Т.к. переменные новой функции принимают значения из множества
, откуда следует, что при суперпозиции вместо переменных некоторой булевой функции могут быть взяты булевы функции. Т.к. переменные новой функции принимают значения из множества 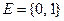 , сама новая функция также будет булевой функцией, т.е. будет принимать значения из множества
, сама новая функция также будет булевой функцией, т.е. будет принимать значения из множества 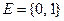 .
.
Теорема Поста: для того чтобы система булевых функций была полной, необходимо и достаточно, чтобы она содержала хотя бы одну функцию:
1. не сохраняющую константу 1;
2. не сохраняющую константу 0;
3. не самодвойственную;
4. не линейную;
5. не монотонную.
Доказательство: если какое-либо из перечисленных условий полноты не будет выполнено, то будем иметь класс булевых функций, который является собственным подмножеством множества 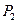 всех булевых функций.
всех булевых функций.
| Функция | K0 | K1 | L | M | S |
| Отрицание | – | – | + | – | + |
| Дизъюнкция | + | + | – | + | – |
| Конъюнкция | + | + | – | + | – |
| Импликация | – | + | – | – | – |
| Сложение по модулю 2 | + | – | + | – | – |
| Эквивалентность | – | + | + | – | – |
Из таблицы можно определить, что системы булевых функций, содержащие отрицание и конъюнкцию, отрицание и дизъюнкцию, являются функционально полными. Естественно, полной будет и система, содержащая отрицание, конъюнкцию и дизъюнкцию.
Алгебра Жегалкина.
Определение 9.4. Система элементов 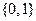 , на которой определены операции конъюнкция и сложение по модулю 2 и для которой выполняются соотношения:
, на которой определены операции конъюнкция и сложение по модулю 2 и для которой выполняются соотношения:
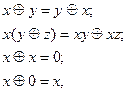
называется алгеброй Жегалкина.
Мета определения:
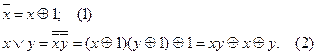
Определение 9.5. Всякая формула алгебры Жегалкина, имеющая вид суммы по сложению по модулю 2 конъюнкций булевых переменных, называется полиномом Жегалкина.
Определение 9.6. Если в каждый член полинома Жегалкина каждая переменная входит один раз и полином не содержит одинаковых членов, то такой полином Жегалкина называется каноническим или бисуммарной нормальной формой.
Теорема: всякая булева функция единственным образом представима в виде канонического полинома Жегалкина или в виде совершенной бисуммарной нормальной формы (СБНФ).
Доказательство: всякую булеву формулу можно представить в виде полинома Жегалкина, используя мета определения (1) и (2). Из метаопределения (2) следует, что если две функции 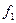 и
и 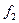 таковы, что
таковы, что 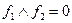 , то
, то 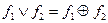 . Отсюда следует правило для представления булевой функции в виде полинома Жегалкина: для булевой формулы, заданной в виде СДНФ, достаточно:
. Отсюда следует правило для представления булевой функции в виде полинома Жегалкина: для булевой формулы, заданной в виде СДНФ, достаточно:
- заменить знак 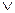 на знак
на знак 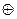 ;
;
- представить отрицания переменных как 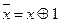 ;
;
- раскрыть скобки по закону дистрибутивности;
- привести подобные члены.
Пример:
приведем к каноническому полиному Жегалкина булеву функцию:
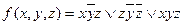 .
.
Поскольку функция находится в СДНФ, заменим символ 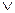 на символ
на символ 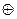 . Получим:
. Получим:
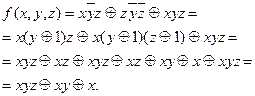
Дата добавления: 2015-12-16; просмотров: 1657;
