УСЛОВИЕ ПЕРЕДАЧИ ИСТОЧНИКОМ МАКСИМУМА МОЩНОСТИ ПРИ ЗАДАННОМ КОЭФФИЦИЕНТЕ МОЩНОСТИ ПРИЕМНИКА

На практике часто возникает необходимость подбора комплекс­ного сопротивления нагрузки таким образом, чтобы при заданных комп­лексном сопротивлении источника и коэффициенте мощности прием­ника обеспечивалась передача ма­ксимума полной и соответственно средней мощности от источника приемнику.

Пользуясь условными обозначе­ниями, принятыми в предыдущем параграфе, находим полную мощ­ность на зажимах нагрузки:

,

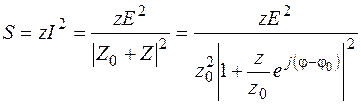где φ и φ₀ - аргументы комплексных со­противлений Z и Z₀.

После преобразования получим:

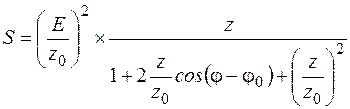. (3.18)

Приняв величину z за перемен­ную, записываем условие максиму­ма функции S

,

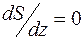откуда

,

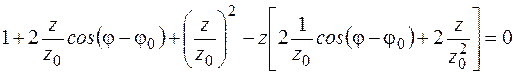или

.

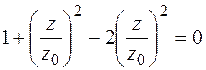Следовательно,

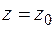. (3.19)

Подстановка (3.19) в (3.18) дает

.

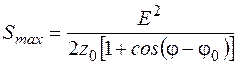Таким образом, передача макси­мума мощности в нагрузку при за­данном cosφ достигается при ра­венстве полных сопротивлений на­грузки и источника. При этом передаваемая мощность тем боль­ше, чем больше разность углов со­противлений нагрузки и источника ôφ - φ₀ô.

Если условие (3.19) не соблюдается, то относительное отклонение передаваемой полной мощности от максимальной состав­ляет

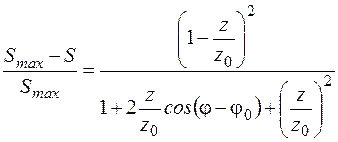. (3.20)

Практически допустимы отклонения от условия (3.19), при которых величина (3.20) не превышает заданного предела.

Условия передачи максимума мощности широко используются в радиотехнике, электропроводной связи, автоматике и приборострое­нии. В энергетических же системах, генерирующих и потребляющих большие мощности, стремятся обес­печить высокий к.п.д. генераторов; поэтому сопротивления нагрузок значительно превышают сопротив­ления генераторов.

БАЛАНС МОЩНОСТЕЙ

Из закона сохранения энергии следует, что для любой электриче­ской цепи соблюдается закон баланса активных мощностей: активная мощность, генерируемая источника­ми, равна активной мощности, по­требляемой всеми приемниками.

В свою очередь можно показать, что сумма отдаваемых реактивных мощностей равна сумме потребляе­мых реактивных мощностей.

Если воспользоваться комплекс­ной формой записи токов, напряже­ний и мощностей, то высказанные положения будут вытекать из сле­дующих рассуждений.

Для электрической цепи, содер­жащей q узлов, можно написать по первому закону Кирхгофа q – 1 уравнений вида

,

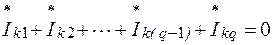где положительные направления всех токов приняты от узла k к уз­лам 1, 2,..., q.

Умножим каждое из этих урав­нений на комплексное напряжение, отсчитываемое от соответствующе­го узла к узлу q, и просуммируем эти произведения

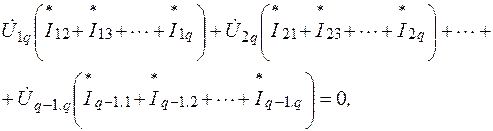
откуда с учетом того, что

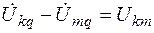
и

,

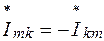получим

.

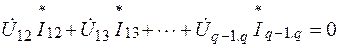Итак, сумма комплексных мощ­ностей, потребляемых всеми ветвя­ми электрической цепи, равна ну­лю; следовательно, также равны нулю в отдельности алгебраические суммы действительных и мнимых частей мощностей.

Иначе говоря, равна нулю как алгебраическая сумма потребляе­мых всеми ветвями цепи средних мощностей, так и алгебраическая сумма потребляемых реактивных мощностей.

Поскольку отрицательные по­требляемые мощности представля­ют собой мощности отдаваемые, то отсюда следует закон баланса как средних, так и реактивных мощ­ностей.

В случае цепи постоянного тока сумма мощностей источников равна сумме мощностей, расходуемых в сопротивлениях, причем знаки мощностей источников определяют­ся по указанному выше правилу:

мощность положительна при совпа­дении направлений ЭДС E и тока I, проходящего через источник, и от­рицательна при встречном направ­лении ЭДС и тока. В последнем случае, если источником энергии служит аккумулятор, то мощность EI расходуется на его зарядку; если же источником служит генератор, то мощность EI расходуется на механическую работу (генератор ра­ботает в режиме двигателя).