ЗАКОНЫ ОМА И КИРХГОФА В КОМПЛЕКСНОЙ ФОРМЕ
Рассмотрим применение метода комплексных амплитуд в случае последовательного и параллельного соединений элементов R, L, С.
Последовательное соединение R, L, С.
Положим, что в уравнении Кирхгофа

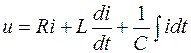 (3.4)
(3.4)
заданными являются параметры R, L, С и гармоническое напряжение u = Umcos(wt+y)на зажимах цепи, а искомой величиной является ток i. Ввиду того, что здесь рассматривается установившийся режим цепи гармонического тока, решение этого дифференциального уравнения должно дать гармоническую функцию вида
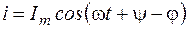 ,
,
где Im и (y – j) – пока неизвестные амплитуда и начальная фаза тока.
Пусть в соответствии с предыдущим параграфом заданное гармоническое напряжение символизируется комплексной функцией 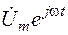 , а искомый гармонический ток – комплексной функцией
, а искомый гармонический ток – комплексной функцией 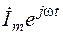 , комплексные амплитуды напряжения и тока равны соответственно:
, комплексные амплитуды напряжения и тока равны соответственно:
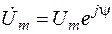 ;
; 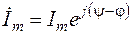 .
.
Сложение, дифференцирование и интегрирование гармонических функций в уравнении (3.4) заменяются теми же математическими операциями над действительными частями комплексных функций:
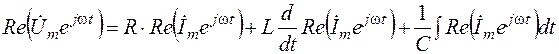 . (3.5)
. (3.5)
Операции над действительными частями комплексных функций могут быть заменены операциями над самими комплексными функциями с последующим выделением действительной части полученного результата. Объясняется это коммутативностью операций сложения, дифференцирования и интегрирования относительно символической операции Re. Итак, (3.5) преобразуется следующим образом:
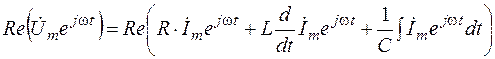 .
.
Полученное уравнение удовлетворяется для любого момента времени. Поэтому заключенные в скобки комплексные выражения, от которых берется действительная часть, должны быть равны друг другу. Производя дифференцирование и интегрирование, получаем:
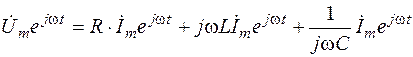 . (3.6)
. (3.6)
Здесь следует обратить внимание на то, что при интегрировании функции еjwt постоянная интегрирования опущена, так как в рассматриваемом установившемся режиме цепи гармонического тока электрические заряды или напряжения на емкостях представляют гармонические функции, не содержащие постоянных слагающих.
В результате сокращения всех частей уравнения (3.6) на множитель еjwt получается алгебраическое комплексное уравнение
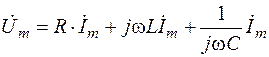 . (3.7)
. (3.7)
Ток Im может быть вынесен за скобки. При этом вводится условное обозначение для комплексного сопротивления рассматриваемой электрической цепи
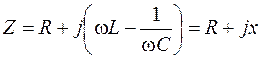 . (3.8)
. (3.8)
Таким образом, получается уравнение
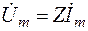 , (3.9)
, (3.9)
выражающее закон Ома для комплексных амплитуд.
Разделив обе части уравнения (3.9) на  , получим закон Ома для комплексных действующих значений
, получим закон Ома для комплексных действующих значений
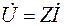 . (3.10)
. (3.10)
Следовательно, комплексное сопротивление электрической цепи равно отношению комплексного напряжения на зажимах данной цепи к комплексному току в этой цепи.
Комплексное сопротивление Z представлено в выражении (3.8) в алгебраической форме. Та же величина в тригонометрической и показательной (полярной) формах имеет вид:
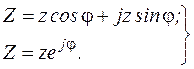 (3.11)
(3.11)
Здесь 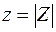 – модуль комплексного числа Z – представляет полное сопротивление цепи, а j - аргумент комплексного числа Z:
– модуль комплексного числа Z – представляет полное сопротивление цепи, а j - аргумент комплексного числа Z:
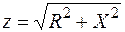 ;
; 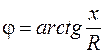 .
.
На основании (3.9) комплексная амплитуда тока
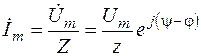 ,
,
где y - φ – начальная фаза тока. Следовательно, искомый ток в тригонометрической форме
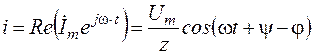 ,
,
что совпадает с результатом, полученным ранее.
На рисунке 3.4 дана геометрическая интерпретация на комплексной плоскости уравнения (3.10). Рисунок 3.4, а относится к случаю, когда реактивное сопротивление цепи имеет индуктивный характер (Х > 0) и соответственно ток отстает по фазе от напряжения (φ > 0). Рисунок 3.4, б относится к случаю, когда реактивное сопротивление цепи имеет емкостный характер (Х < 0), и поэтому ток опережает по фазе напряжение (φ < 0).
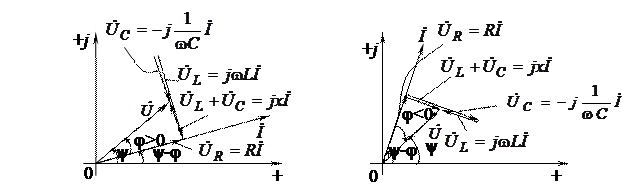
а б
Рисунок 3.4 Векторные диаграммы для последовательной цепи R, L, С
при х > 0(а) и x < 0 (б)
В случае чисто реактивной цепи (R = 0) ток отстает от напряжения по фазе на p/2, если сопротивление цепи индуктивное, и опережает напряжение на p/2 при емкостном сопротивлении цепи.
Как видно из векторных диаграмм, приведенных на рисунке 3.4, UR = RI – напряжение на сопротивлении R (совпадает по фазе с током I), UL = jwLI – напряжение на индуктивности L (опережает ток I на угол p/2) и UC = –jI ×1/(wC) – напряжение на емкости С (отстает от тока I на угол p/2).
Геометрическая сумма векторов  дает вектор приложенного к цепи напряжения
дает вектор приложенного к цепи напряжения
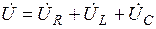 .
.
Активная слагающая напряжения Ua = UR, реактивная слагающая Up = UL + Uc и суммарное напряжение U образуют треугольник напряжений.
Треугольник сопротивлений, подобный треугольнику напряжений и повернутый относительно него на угол y - j (рисунок 3.5), представляет геометрическую интерпретацию уравнений (3.11). Его положение не зависит от начальных фаз  и
и 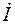 ; сопротивление R откладывается на комплексной плоскости в положительном направлении действительной оси, а реактивное сопротивление х в зависимости от его знака откладывается в положительном (х > 0) или отрицательном (х < 0) направлении мнимой оси (рисунок 3.5, а и б).
; сопротивление R откладывается на комплексной плоскости в положительном направлении действительной оси, а реактивное сопротивление х в зависимости от его знака откладывается в положительном (х > 0) или отрицательном (х < 0) направлении мнимой оси (рисунок 3.5, а и б).
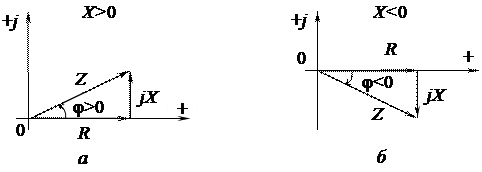
Рисунок 3.5 Треугольник сопротивлений при х > 0 (а) и х < 0 (б)
Параллельное соединение R,L, С.
Пользуясь рассуждениями, аналогичными приведенными выше, можно прийти к комплексной форме законов Ома и Кирхгофа для электрической цепи, состоящей из элементов R, L и С, соединенных параллельно.
Ограничиваясь записью для комплексных действующих значений, пропорциональных комплексным амплитудам, имеем в соответствии с первым законом Кирхгофа
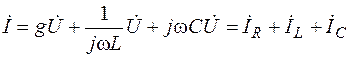 ; (3.12)
; (3.12)
здесь 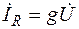 – ток в сопротивлении R (совпадает по фазе с напряжением U);
– ток в сопротивлении R (совпадает по фазе с напряжением U);
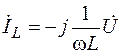 – ток в индуктивности (отстает от напряжения на p/2);
– ток в индуктивности (отстает от напряжения на p/2);
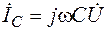 – ток в емкости (опережает напряжение на p/2).
– ток в емкости (опережает напряжение на p/2).
Выражение
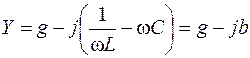 (3.13)
(3.13)
представляет собой комплексную проводимость рассматриваемой цепи; g и b – активная и реактивная проводимости цепи.
Уравнение
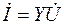 (3.14)
(3.14)
выражает закон Ома в комплексной форме. Следовательно, комплексная проводимость электрической цепи равна отношению комплексного тока в данной цепи к комплексному напряжению на ее зажимах.
Тригонометрическая и показательная (полярная) формы комплексной проводимости имеют следующий вид:
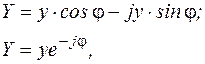
здесь 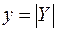 – модуль комплексного числа Y – представляет полную проводимость цепи, а (-φ) – аргумент комплексного числа Y:
– модуль комплексного числа Y – представляет полную проводимость цепи, а (-φ) – аргумент комплексного числа Y:
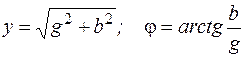 .
.
На основании (3.14) комплексное действующее значение тока равно
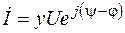 ,
,
что соответствует гармоническому току
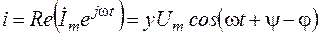 .
.
На рисунке 3.6 дана геометрическая интерпретация на комплексной плоскости уравнения (3.12). Рисунок 3.6, а относится к случаю, когда реактивная проводимость цепи имеет индуктивный характер (b > 0) и соответственно ток отстает по фазе от напряжения (φ > 0). Рисунок 3.6, б относится к случаю, когда реактивная проводимость цепи имеет емкостный характер (b < 0) и соответственно ток опережает по фазе напряжение (φ < 0).
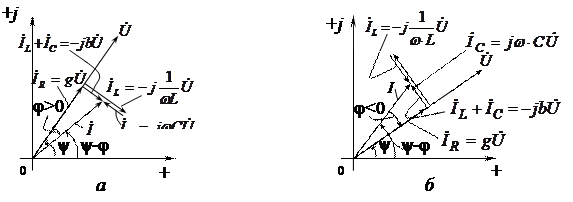
Рисунок 3.6 Векторные диаграммы для параллельной цепи R, L, С
при b > 0 (а) и b < 0 (б)
Активная слагающая тока Ia = IR, реактивная слагающая Ip =IL + IC и суммарный ток I образуют треугольник токов.
Треугольник проводимостей, подобный треугольнику токов и повернутый относительно последнего на угол y против хода часовой стрелки (рисунок 3.7), служит геометрической интерпретацией выражения (3.13): активная проводимость g откладывается на комплексной плоскости в положительном направлении действительной оси, а реактивная проводимость b в зависимости от ее знака откладывается в отрицательном (b > 0) или положительном (b < 0) направлении мнимой оси (рисунок 3.7, а и б).
|
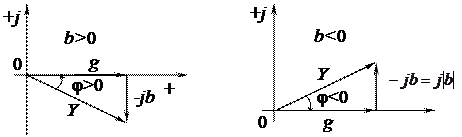
а б
Рисунок 3.7 Треугольник проводимостей при b > 0 (а) и b < 0 (б)
В таблице 3.1 дана сводка уравнений элементов цепи в комплексной форме.
Таблица 3.1 Комплексная запись уравнений элементов цепи
| Элемент | Напряжение | Ток |
| Сопротивление | 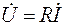
| 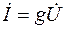
|
| Индуктивность | 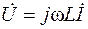
| 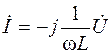
|
| Емкость | 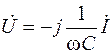
| 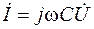
|
Следует обратить внимание на то, что комплексное сопротивление индуктивного элемента равно jwL, а емкостного элемента равно 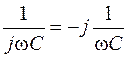 ; комплексная проводимость составляет соответственно:
; комплексная проводимость составляет соответственно:
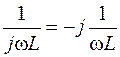 и
и 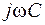 .
.
При последовательном соединении R, L и С складываются в комплексной форме сопротивления, а при параллельном соединении – проводимости.
В таблице 3.2 приведены выражения комплексных сопротивлений и проводимостей цепи для различных сочетаний элементов R , L, С.
Таблица 3.2 Выражение комплексных сопротивлений
и проводимостей
| Цепь | Z при последовательном соединении | Y при параллельном соединении |
| R, L | 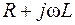
| 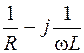
|
| R, C | 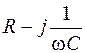
| 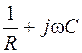
|
| R, L, C | 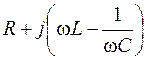
| 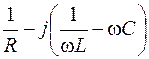
|
Дата добавления: 2015-12-16; просмотров: 2066;
