Непараметрические методы. Непараметрические методы не основываются на оценке параметров

Непараметрические методы не основываются на оценке параметров. Они разработаны для тех ситуаций, достаточно часто возникающих на практике, когда исследователь ничего не знает о параметрах исследуемой выборки. Поэтому эти методы иногда также называются свободными от параметров или свободно распределенными.

Подход без использования критериев оценки альтернатив позволяет:

· сформировать множество альтернативных вариантов решения;

· получить результаты сравнения (например, попарного) альтернатив;

· выбрать лучшую альтернативу, которая и выдается системой в качестве рекомендации.

По существу, для каждого параметрического критерия имеется, по крайней мере, один непараметрический аналог. Эти критерии можно отнести к одной из следующих групп:

· критерии различия между группами (независимые выборки);

· критерии различия между группами (зависимые выборки);

· критерии зависимости между переменными.

В качестве непараметрического способа упорядочения могут применять ранжирование. Оценки, присваиваемые при ранжировке, называют рангами. В такой методике одинаковые ранги могут иметь разные альтернативы. В этом случае ранжировка называется нестрогой. При строгой ранжировке каждой альтернативе присваивается уникальный ранг.

При наличии дискретных экспертных кривых, созданных на аналитической основе с использованием экономико-математических методов, эксперту позволяют выбрать предпочтительный вариант.

Анализ альтернатив в этом случае становится важнейшим этапом разработки решения, так как выбранные альтернативы еще предстоит оценить, проанализировать и отобрать лучшие из них (рис. 3.14).

Рис. 3.14. Методы анализа альтернатив

Непосредственная количественная оценка используется в двух случаях:

а) когда необходимо экспертно определить значение показателя путем сбора мнений экспертов о числовом предполагаемом значении показателя или о диапазоне, в который он должен уложиться;

б) когда необходимо оценить степень сравнительной предпочтительности объекта в баллах.

Метод средней точкиприменяется, когда есть возможность определить значение признака как промежуточное по формуле 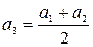, а значение 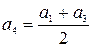и т.д.

Метод Акоффаиспользуется при количественной оценке сравнительной предпочтительности альтернативных вариантов и допускает корректировку оценок, даваемых экспертами. Все варианты ранжируются по предпочтительности, каждому из них в долях единицы дается количественная оценка. Вариант определяется числом и его количественной весовой оценкой. Эксперт сопоставляет вариант и сумму остальных альтернативных вариантов и делает предпочтение.

Метод лотерейоснован на том, что берется любая тройка альтернативных вариантов а₁, а₂и а₃, упорядоченных в порядке убывания предпочтительности, и эксперт указывает такую вероятность р, при которой а₂=а; р=а₃(1- р).

Формула позволяет сравнивать по предпочтительности варианты, имеющие различные степени реализации.

Суть экспертной классификации- отнесение варианта к какому-нибудь сорту, классу, уровню, категории. Эксперт получает объект (его описание) и относит его к определенному классу и т.д., и так по всем объектам с последующей корректировкой всей картины в целом.

Метод парных сравненийоснован на попарном сравнении первого решения со вторым, выбранного из них с третьим, выбранного из этой пары со следующим, и так до оценки всей совокупности решений.

Ранжировка альтернативных вариантовзаключается в выборе экспертом по определенным критериям первого предпочтительного варианта, затем из оставшегося списка – снова одного наиболее предпочтительного и т.д.