Примеры описательных моделей
| Тип задачи | Вид модели | Математический метод решения |
| Задачи планирования без оптимизации (расчет объемов производства по видам продукции, увязка планов производства с ресурсами и т.п.) | Балансовые модели | Аппарат линейной алгебры, матричное исчисление |
| Задачи сетевого планирования и управление (СПУ) без оптимизации | Расчет по формулам модели СПУ | Аппарат теории графов |
| Задача учета и статистики (оперативный учет, получение различных форм отчетности и т.п.) | Расчет по формулам | |
| Задачи контроля и анализа (анализ влияния и факторов, выявление тенденций, отслеживание отклонений и установление их причин) | Статистические модели обработки реализаций случайных величин | Факторный анализ, дисперсионный анализ, регрессионный анализ |
| Задача создания нормативной базы | Статистические модели обработки реализаций случайных величин | То же |
| Расчет параметров функционирования сложных систем с неформализованными связями | Расчет по формулам имитационных моделей | То же |
| Задачи прогнозирования | Модели регрессионного анализа, оценка параметров и проверка статистических гипотез | Факторный анализ, дисперсионный анализ, регрессионный анализ, аппарат математической статистики |
| Прочие задачи, связанные с рутинными процессами переработки информации, т.е. с расчетами по заданным формулам (расчеты подетальных спецификаций, потребности в оборудовании и производственных площадях и другие расчеты технической подготовки производства) |
В зависимости от степени формализованности связей f и gi между факторами моделей в выражениях (2.4) и (2.5) различают аналитические и алгоритмические модели.
Аналитической формой записи называется запись математической модели в виде алгебраических уравнений или неравенств, не имеющих разветвлений вычислительного процесса при определении значений любых переменных состояния модели, целевой функции и уравнений связи. Если в математических моделях единственная целевая функция f и ограничения gj заданы аналитически, то подобные модели относятся к классу моделей математического программирования. Характер функциональных зависимостей, выраженных в функциях f и gj , может быть линейным и нелинейным. Соответственно этому ЭММ делятся на линейные и нелинейные, а среди последних в специальные классы выделяются дробно-линейные, кусочно-линейные, квадратичные и выпуклые модели.
Если мы имеем дело со сложной системой, то зачастую гораздо легче построить ее модель в виде алгоритма, показывающего отношения между элементами системы в процессе ее функционирования, задаваемые обычно в виде логических условий – разветвлений хода течения процесса. Математическое описание для элементов может быть очень простым, однако взаимодействие большого количества простых по математическому описанию элементов и делает эту систему сложной. Алгоритмически же можно описывать даже такие объекты, которые в силу их сложности или громоздкости в принципе не допускают аналитического описания. В связи с этим к алгоритмическим моделям относятся такие, в которых критерии и (или) ограничения описываются математическими конструкциями, включающими логические условия, приводящие к разветвлению вычислительного процесса. К алгоритмическим моделям относятся и так называемые имитационные модели – моделирующие алгоритмы, имитирующие поведение элементов изучаемого объекта и взаимодействие между ними в процессе функционирования.
В зависимости от того, содержит ли ЭММ случайные факторы, она может быть отнесена к классу стохастических или детерминированных.
В детерминированных моделях ни целевая функция f , ни уравнения связи gj не содержат случайных факторов. Следовательно, для данного множества входных значений модели на выходе может быть получен только один-единственный результат. Для стохастических ЭММ характерно наличие среди факторов 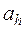 модели, описываемой соотношениями (2.4) и (2.5), таких, которые имеют вероятностную природу и характеризуются какими-либо законами распределения, причем среди функций f и gj могут быть и случайные функции. Значения выходных характеристик в таких моделях могут быть предсказаны только в вероятностном смысле. Реализация стохастических ЭММ в большинстве случаев осуществляется на ЭВМ методами имитационного статистического моделирования.
модели, описываемой соотношениями (2.4) и (2.5), таких, которые имеют вероятностную природу и характеризуются какими-либо законами распределения, причем среди функций f и gj могут быть и случайные функции. Значения выходных характеристик в таких моделях могут быть предсказаны только в вероятностном смысле. Реализация стохастических ЭММ в большинстве случаев осуществляется на ЭВМ методами имитационного статистического моделирования.
Следующим признаком, по которому можно различать ЭММ, является связь с фактором времени. Модели, в которых входные факторы, а следовательно, и результаты моделирования явно зависят от времени, называются динамическими, а модели, в которых зависимость от времени t либо отсутствует совсем, либо проявляется слабо или неявно, называют статическими. Интересны в этом отношении имитационные модели: по механизму функционирования они являются динамическими (в модели идет имитация работы объекта в течение некоторого периода времени), а по результатам моделирования – статическими (например, определяется средняя производительность объекта за моделируемый период времени).
Статические модели представляют собой известную степень приближения к реальным объектам и системам, функционирующим во времени. Во многих случаях степень такого приближения, проявляющаяся в допущениях о неизменности или различного рода осреднениях факторов во времени (косвенно или приблизительно учитывающих фактор времени в определенных границах его изменения), является достаточной для практического применения статических моделей.
Дата добавления: 2015-12-16; просмотров: 3184;
