Общая характеристика проблемы проектирования систем

Моделирование начинается с формирования предмета исследований – системы понятий, отражающей существенные для моделирования характеристики объекта. Эта задача является достаточно сложной, что подтверждается различной интерпретацией в научно-технической литературе таких фундаментальных понятий, как система, модель, моделирование. Подобная неоднозначность не говорит об ошибочности одних и правильности других терминов, а отражает зависимость предмета исследований (моделирования) как от рассматриваемого объекта, так и от целей исследования; оно становится неотъемлемой частью всего жизненного цикла системы. Объясняется это в первую очередь технологичностью моделей, реализованных на базе средств вычислительной техники: достаточно высокой скоростью получения результатов моделирования и их сравнительно невысокой себестоимостью [39].

Модель может быть подробно обоснована на словесном уровне. Это именно модель, т.е. созданное в результате умственного усилия представление о реальном бизнес-процессе. Словесная модель сформулирована достаточно убедительно для того, чтобы на ее основе разрабатывать, принимать и выполнять ряд управленческих решений [26].

При более тщательном анализе ситуации словесных моделей, как правило, недостаточно. Необходимо применение достаточно сложных математических моделей. Так, при принятии решений в менеджменте производственных систем используются:

· модели технологических процессов (прежде всего модели контроля и управления);

· модели обеспечения качества продукции (в частности, модели оценки и контроля надежности);

· модели массового обслуживания;

· модели управления запасами (модели логистики);

· имитационные и эконометрические модели деятельности предприятия в целом и др.

В процессе подготовки и принятия решений часто используют имитационные модели и системы. Имитационная модель позволяет отвечать на вопрос: "что будет, если…?" Это совокупность моделей, имитирующих протекание изучаемого процесса, объединенная со специальной системой вспомогательных компьютерных программ и информационной базой, позволяющих достаточно просто и оперативно реализовать вариантные расчеты.

Большинство моделей содержит различные параметры. Упрощенно построение модели можно рассматривать как выбор набора параметров и организацию связи между ними. Параметры могут отличаться качественно и количественно [5, 37, 52].

Выражение, состоящее из совокупности связанных между собой математических зависимостей (формулы, уравнения, неравенства, логические условия величин – факторов), все или часть которых имеют экономический смысл, называется экономико-математической моделью (ЭММ). По своей роли в ЭММ эти факторы целесообразно подразделить на параметры и характеристики (рис. 2.1).

Рис. 2.1. Классификация факторов по их роли в ЭВМ

При этом параметрами объекта называются факторы, характеризующие свойства объекта или составляющих его элементов. В процессе исследования объекта ряд параметров может изменяться, поэтому они называются переменными, которые, в свою очередь, подразделяются на переменные состояния и переменные управления. Как правило, переменные состояния объекта являются функцией переменных управления и воздействий внешней среды. Характеристиками (выходными характеристиками) называются интересующие исследователя непосредственные конечные результаты функционирования объекта (естественно, что выходные характеристики являются переменными состояния). Соответственно характеристики внешней среды описывают свойства внешней среды, которые сказываются на процессе и результате функционирования объекта. Значения ряда факторов, определяющие начальное состояние объекта или внешней среды, называются начальными условиями.

Критерием оптимальности называется некоторый показатель, имеющий экономическое содержание, служащий формализацией конкретной цели управления и выражаемый при помощи целевой функции через факторы модели. Критерий оптимальности определяет смысловое содержание целевой функции. В ряде случаев в качестве критерия оптимальности может выступать одна из выходных характеристик объекта.

Целевая функция математически связывает между собой факторы модели, ее значение определяется значениями этих величин. Содержательный смысл целевой функции придает только критерий оптимальности.

Не следует смешивать критерий оптимальности и целевую функцию. Так например, критерии прибыли и стоимости произведенной продукции могут описываться одной и той же целевой функцией:

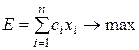, (2.2)

где 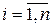– номенклатура производимой продукции; 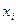– объем выпуска i-й номенклатуры; 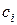– прибыль от выпуска единицы i-й номенклатуры или стоимость единицы i-й номенклатуры в зависимости от смысла критерия оптимальности.

Критерий прибыли может рассчитываться и по нелинейной целевой функции:

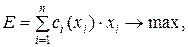(2.3)

если прибыль от выпуска единицы i-й номенклатуры является функцией от объема выпуска .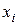

При наличии нескольких критериев оптимальности каждый из них будет формализован своей частной целевой функцией 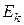, где 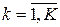– число критериев оптимальности. Для однозначного выбора оптимального решения исследователь может сформулировать новую целевую функцию

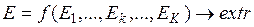. (2.4)

Однако целевая функция может уже не нести экономического смысла, в этом случае критерий оптимальности для нее отсутствует.

Система ограничений определяет пределы, сужающие область осуществимых, приемлемых или допустимых решений и фиксирующие основные внешние и внутренние свойства объекта. Ограничения определяют область протекания процесса, пределы изменения параметров и характеристик объекта.

Уравнения связи являются математической формализацией системы ограничений. Между понятиями "система ограничений" и "уравнения связи" существует точно такая же аналогия, как между понятиями "критерий оптимальности" и "целевая функция": различные по смыслу ограничения могут описываться одинаковыми уравнениями связи, а одно и то же ограничение в разных моделях записываться различными уравнениями связи.

Таким образом, именно критерий оптимальности и система ограничений в первую очередь определяют концепцию построения будущей математической модели, т.е. концептуальную модель, а их формализация, т.е. целевая функция и уравнения связи представляют собой математическую модель.

Решением математической модели называется такой набор (совокупность) значений переменных, который удовлетворяет ее уравнениям связи. Решения, имеющие экономический смысл, называют структурно допустимыми. Модели, имеющие много решений, называются вариантными в отличие от безвариантных, имеющих одно решение. Среди структурно допустимых решений вариантной модели, как правило, находится одно решение, при котором целевая функция в зависимости от смысла модели имеет наибольшее или наименьшее значение. Такое решение, как и соответствующее значение целевой функции, называется оптимальным (в частности, наименьшим или наибольшим).

Использование ЭММ, особенно оптимальных, предполагает не только построение модели, соответствующей поставленной задаче, но и ее решение при помощи подходящего метода. В связи с этим иногда под моделированием (в узком смысле) понимается этап нахождения решения модели, т.е. вычисления значений исследуемых характеристик и определение оптимальности различных вариантов изучаемого объекта с целью выбора наилучшего варианта его построения и функционирования. Данный этап представляет собой реализацию и исследование ЭММ на определенном наборе вычислительных средств. Выбор метода решения оптимизационных ЭММ зависит от математической формы, связывающей факторы модели, наличия тех или иных признаков (учет динамики, учет стохастичности и т.д.). С точки зрения корректного выбора метода решения модели наиболее существенными признаками являются характер цели исследования, формализованность связей между параметрами и характеристиками, учет вероятностной природы объекта, а также фактора времени.

По характеру цели исследования ЭММ делятся на оптимизационные (нормативные) и описательные (дескриптивные или ЭММ прямого счета).

Характерной чертой оптимизационных моделей является наличие одной или нескольких целевых функций. При этом в первом случае оптимизационные ЭММ называются монокритериальными, а во втором – многокритериальными. В общем виде монокритериальная ЭММ может быть представлена следующей системой отношений:

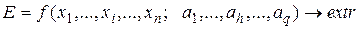; (2.5)

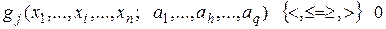, (2.6)

где Е – критерий оптимальности объекта; 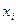– управляемые переменные, 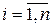; 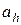– неуправляемые факторы модели; 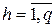; 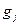– уравнения связи, представляющие собой формализацию системы ограничений, 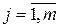; 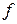– целевая функция – формализованное выражение критерия оптимальности.

Выражение 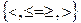означает, что в ограничениях может стоять любое из приведенных в фигурных скобках логических условий.

Решение модели, заданной соотношениями (2.5) и (2.6), заключается в нахождении совокупности значений переменных

,

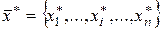обращающей в max (или min) целевую функцию Е при заданных уравнениях связи .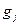

Специфика конкретных задач управления производством определила разнообразие типов оптимизационных ЭММ. Для ряда наиболее часто повторяющихся типов ситуаций это вызвало разработку "стандартных" экономико-математических методов их описания, например, распределительные задачи различных классов, задачи управления запасами, ремонта и замены оборудования, проектирования сетей и выбора маршрутов и т.д.

Существенным признаком описательных моделей является отсутствие в них критерия оптимальности. Решение, даваемое ЭММ прямого счета, обеспечивает либо вычисление набора выходных характеристик объекта для одного или нескольких вариантов начальных условий и входных характеристик объекта, либо нахождение какой-либо совокупности значений в структурно допустимой области решений. Примеры типовых задач управления производством, решаемых с помощью описательных моделей, приведены в табл. 2.1.

Таблица 2.1