Часть 2. Модели и моделирование при принятии решений

Одной из проблем, с которой сталкиваются специалисты при проверке качества управления какой-либо системой, является проблема эксперимента. Для определения параметров системы можно использовать статистические данные, наблюдения или измерения. Но при исследовании поведения системы в динамике требуется проведение эксперимента.

Эксперимент при исследовании новых методов чреват своей непредсказуемостью. Не стоит упоминать, что иногда его проведение нарушает законы морали или безопасности, связано с материальными затратами и значительными потерями информации.

Опыт человеческой деятельности подсказывает проводить вместо реальных дорогостоящих и порой небезопасных экспериментов над объектом исследование его моделей и применение моделирования при изучении его динамики.

Под термином "модель" не надо понимать обязательно модель физическую, т.е. копию объекта в уменьшенном или увеличенном виде. В большинстве случаев реальные процессы можно моделировать методами математики. Поэтому чаще всего приходится прибегать к математическому моделированию.

В то же время математическое моделирование означает всего лишь формализацию и исследование объекта методами математики.

Определяющим при построении модели является не форма ее представления, а соответствие реальному объекту и его поведению в реальной обстановке.

В реальных системах возможен адекватный выбор элементов моделей. Эта адекватность может быть без проблем экспериментально проверена для отдельных элементов системы. Но уже для подсистем, а тем более системы в целом, существует возможность серьезной методической ошибки, связанная с объективной невозможностью оценить адекватность модели большой системы на логическом уровне.

Один из принципов построения моделей, в частности, их элементов, носит название "минимальной достаточности" и требует построения их минимально простыми, насколько это возможно без потери сущности. Взаимодействие десятков, сотен элементов моделей создает дополнительные эффекты и последствия, которые сложно предугадать.

Можно построить логически безупречную модель реальной системы с использованием моделей элементов и производить анализ такой модели. Но при их взаимодействии возможны ситуации, непредсказуемые с позиций первоначального математического описания. Именно это требует дополнительно к построению модели проведение модельного эксперимента применительно к условиям реального функционирования объекта.

Другой причиной проведения модельного эксперимента является отсутствие информации. С позиции теории информации моделирование уменьшает или устраняет информационную неопределенность во всех областях решения задачи. По этой причине область решения задач разбивают на более мелкие, для которых можно строить адекватные модели. Существуют разные подходы использования моделей для поддержки принятия решений. Один из общих подходов к построению модели основан на аналитическом описании изучаемой системы или объекта управления. Модель изучаемой системы в общем виде можно представить в виде зависимости:

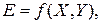(2.1)

где E – критерий эффективности – количественный показатель эффективности системы в плане достижения цели Т; Х – управляющие воздействия – управляемые переменные системы, на которые ЛПР может воздействовать; Y – состояния внешней среды (природы) – неуправляемые возможные или вероятностные, внешние по отношению к системе воздействия.

Возможны ситуации (как правило, жестко детерминированные или информационно определенные), в которых нет необходимости учитывать вероятностные состояния природы. В таком случае принято говорить о принятии управляющих решений или об управлении в условиях определенности.

Если воздействие окружающей среды значимо и не определено однозначно, то приходится управлять системой в условиях неопределенности или при наличии противодействия.

Рассмотрим первую ситуацию. Одним из распространенных методов поддержки принятия решений для таких ситуаций является метод, основанный на исследовании операций и последующем построении моделей, чаще всего экономико-математических.