Программа решения задачи.
Предлагается решить задачу в интерактивном режиме, вводя команды в окно ANSYS Input и отслеживая получаемые результаты.
/PREP7 ! Вход в препроцессор
/UNITS, SI ! Задать единицы измерения СИ !* Геометрические параметры рамы
c=2
a=2
b=4
!* Геометрические параметры сечения
B1=0.01
H1=0.03
!* Задание ключевых точек
K,1,0,0,0,
K,2,0,0,c,
K,3,b+2*a,0,0,
K,4,b+2*a,0,c,
K,5,a,0,c,
K,6,a,0,0,
K,7,a+b,0,0,
K,8,a+b,0,c,
! Ключевые точки, образующие дуги окружности
K,9,a,c/2,c/2,
K,10,a+b,c/2,c/2, K,11,a,c*(sqrt(2)/4),c/2-c*(sqrt(2)/4), K,12,a,c*(sqrt(2)/4),c/2+c*(sqrt(2)/4), K,13,a+b,c*(sqrt(2)/4),c/2-c*(sqrt(2)/4), K,14,a+b,c*(sqrt(2)/4),c/2+c*(sqrt(2)/4), !* Действующие нагрузки
P=1000
q=100
!* Задание линий
LSTR, 2, 5
LSTR, 5, 8
LSTR, 8, 4
LSTR, 4, 3
LSTR, 3, 7
LSTR, 7, 6
LSTR, 6, 1
LSTR, 1, 2
LSTR, 5, 6
LSTR, 8, 7
LSTR, 3, 4
LSTR, 9, 10
! Построение дуг – сплайнов
SPLINE,5,12,9,11,6
SPLINE,8,14,10,13,7
! Склеивание линий
! Операция склеивания необходима для того, чтобы ANSYS воспринимал
! конструкцию, как единое целое
LGLUE,ALL
! Задание свойств материала
UIMP,1,EX, , ,2e11, ! Модуль Юнга первого материала UIMP,1,DENS, , ,7800, ! Плотность первого материала UIMP,1,NUXY, , ,0.3, ! Коэффициент Пуассона первого материала UIMP,2,EX, , ,2.9e10, ! Модуль Юнга второго материала UIMP,2,DENS, , ,2700, ! Плотность второго материала UIMP,2,NUXY, , ,0.3, ! Коэффициент Пуассона второго материала ! Задание параметров экрана – косоугольная проекция
/VIEW, 1 ,1,2,3 /ANG, 1 /REP,FAST
LPLOT ! Прорисовать линии
!* Задание типа элемента – элемент пространственный балочный BEAM4
ET,1,BEAM4
!* Задание опций элемента
KEYOPT,1,2,0
KEYOPT,1,6,0
KEYOPT,1,7,0
KEYOPT,1,9,9 ! 9 промежуточных точек для построения эпюр
KEYOPT,1,10,0
!* Задание констант элемента. Сечение первое
! Через запятую заданы:
! Площадь сечения: B1*H1
! Момент инерции сечения Izz: (B1*H1**3)/12
! Момент инерции сечения Iyy: (H1*B1**3)/12
! Высота сечения вдоль оси z: B1
! Высота сечения вдоль оси y: H1
! Угол поворота сечения вдоль продольной оси: -90
! Начальная деформация: 0
! Момент инерции сечения Ixx: (H1*B1**3)/12+(B1*H1**3)/12 R,1, B1*H1, (H1*B1**3)/12, (B1*H1**3)/12, H1, B1, -90 , RMORE, ,(B1*H1**3)/12+(H1*B1**3)/12, , , , ,
!* Задание констант элемента. Сечение второе
R,2, B1*B1, (B1**4)/12, (B1**4)/12, B1, B1, , RMORE, ,(B1**4)/6, , , , ,
!* Присвоение атрибутов линии и числа разбиений на элементы
LSEL,S,LOC,Y,0 ! Выделить линию
! Присвоить атрибуты: материал, номер констант, номер типа элемента
LATT, 1, 1, 1, 0
LESIZE,ALL, , ,10,1, ! Присвоить число разбиений на элементы: 10 на линию
!*
LSEL,INVE ! Обратить выделение LATT, 2, 2, 1, 0 ! Присвоить атрибуты
LESIZE,ALL, , ,5,1, ! Присвоить число разбиений на элементы: 5 на линию
ALLSEL,ALL ! Выделить все
LMESH,ALL ! Построить сетку FINISH ! Выход из препроцессора
Группа операторов управления экраном, позволяющая просмотреть построенное сечение балки и присвоенные атрибуты.
! *******
/PNUM,MAT,1 ! Пронумеровать линии по свойствам материала /ESHAPE,1.0 ! Показать форму сечения
/REPLOT ! Перерисовать
! ******
Замечание.
На этом этапе для контроля зайдите в Utility Menu > PlotCtrls > Pan Zoom Rotate. В
меню Pan Zoom Rotate выберем Box Zoom и растянем мышью область около какого-либо узла. Получим следующую картину.
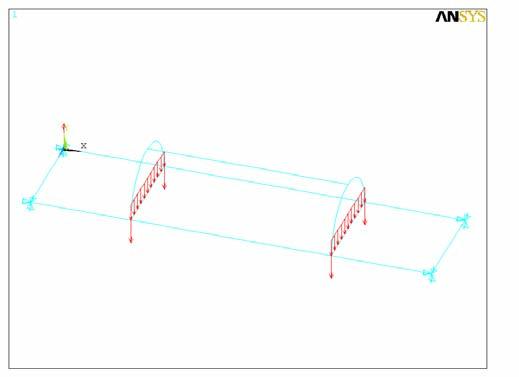
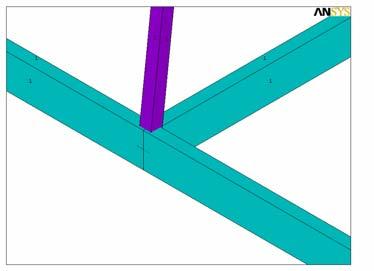
/SOLU ! Вход в процессор решения !* Условия закрепления узлов
! Выделить узел с координатами (0, 0, 0) NSEL,S,LOC,X,0
NSEL,R,LOC,Y,0
NSEL,R,LOC,Z,0
! Закрепить у всех (ALL) выделенных узлов степени свободы UX,UY,UZ D,ALL, , , , , ,UX,UY,UZ
! Выделить узел с координатами (0, 0, с)
NSEL,S,LOC,X,0
NSEL,R,LOC,Y,0
NSEL,R,LOC,Z,C
! Закрепить у всех (ALL) выделенных узлов степени свободы UX,UY,UZ D,ALL, , , , , ,UX,UY,UZ
! Выделить узел с координатами (b+2*a, 0, 0)
NSEL,S,LOC,X,B+2*A
NSEL,R,LOC,Y,0
NSEL,R,LOC,Z,0
! Закрепить у всех (ALL) выделенных узлов степени свободы UX,UY,UZ D,ALL, , , , , ,UX,UY,UZ
! Выделить узел с координатами (b+2*a, 0, с)
NSEL,S,LOC,X,B+2*A
NSEL,R,LOC,Y,0
NSEL,R,LOC,Z,C
! Закрепить у всех (ALL) выделенных узлов степени свободы UX,UY,UZ D,ALL, , , , , ,UX,UY,UZ
!* Задание локальных нагрузок
! Выделить узел с координатами (a, 0, 0) NSEL,S,LOC,X,A
NSEL,R,LOC,Z,0
NSEL,R,LOC,Y,0
! Приложить нагрузку по координате Y величины -P F,ALL,FY,-P,
! Выделить узел с координатами (a, c, 0) NSEL,S,LOC,X,A
NSEL,R,LOC,Z,C
NSEL,R,LOC,Y,0
! Приложить нагрузку по координате Y величины -P F,ALL,FY,-P
! Выделить узел с координатами (a+b, 0, 0) NSEL,S,LOC,X,A+B
NSEL,R,LOC,Z,0
NSEL,R,LOC,Y,0
! Приложить нагрузку по координате Y величины -P F,ALL,FY,-P
! Выделить узел с координатами (a+b, c, 0) NSEL,S,LOC,X,A+B
NSEL,R,LOC,Z,C
NSEL,R,LOC,Y,0
! Приложить нагрузку по координате Y величины -P F,ALL,FY,-P
ALLSEL,ALL
LSWRITE,1, ! Записать приложенную нагрузку, как первый шаг нагружения
! *********
! Приложение распределенной нагрузки
! *********
Распределенная нагрузка прикладывается только на элементы, но элементы можно выделить, только зная, на которой линии они находятся. Поэтому:
LSEL,S,LOC,X,a ! Выделяем слой с координатой X = a LSEL,A,LOC,X,a+b ! Добавляем слой с координатой X = a + b LSEL,R,LOC,Y,0 ! Из слоя выделяем линии с координатой Y = 0 ESLL,S ! Выделяем элементы на выделенных линиях SFBEAM,ALL,1,PRES,q,q, , , , , ! Приложить распределенную нагрузку
ALLSEL, ALL ! Выделить все
LSWRITE,2, ! Записать, как второй шаг нагружения
! Учет веса в ANSYS производится с помощью задания поля ускорений
! В данном случае по Y: 9,8
ACEL,0,9.8,0, ! Ускорение по X, Y, Z
LSWRITE,3, ! Записать, как третий шаг нагружения !* Запуск на решение
LSSOLVE,1,3,1, ! Решать, используя пошаговое нагружение с 1 по 3 с шагом 1 FINISH ! Выход из процессора решения
!* Вход в постпроцессор
/POST1
! Результаты постпроцессорной обработки,
! вводить поблочно в окно ANSYS Input
! Первый шаг нагружения – только узловые силы SET,FIRST ! Считать первый ряд рассчитанных результатов PLDISP,1 ! Показать деформированную форму PLNSOL,U,Y,0,1 ! Показать перемещения вдоль OY
! Второй шаг нагружения – узловые силы + распределенная нагрузка SET,NEXT ! Считать следующий ряд результатов
PLNSOL,U,Y,0,1 ! Показать перемещения вдоль OY
! Третий шаг нагружения – узловые силы + распределенная нагрузка + учет веса SET,NEXT ! Считать следующий ряд результатов
PLNSOL,U,Y,0,1 ! Показать перемещения вдоль OY
! Следующие операторы служат для построения эпюр
! и могут быть использованы после любого шага считывания
!* Задать таблицу значений: максимальные напряжения
ETABLE, SMAXI, NMISC, 1
ETABLE, SMAXJ, NMISC, 21
PLLS, SMAXI,SMAXJ ! Построить графически эпюры
!* Задать таблицу значений: усилия вдоль OX в глобальной системе координат
ETABLE,FXI,SMISC,1
ETABLE,FXJ,SMISC,61
PLLS, FXI, FXJ ! Построить графически эпюры
!* Задать таблицу значений: усилия вдоль OY в глобальной системе координат
ETABLE,FYI,SMISC,2
ETABLE,FYJ,SMISC,62
PLLS,FYI,FYJ ! Построить графически эпюры
!* Задать таблицу значений: усилия вдоль OZ в глобальной системе координат
ETABLE,FZI,SMISC,3
ETABLE,FZJ,SMISC,63
PLLS,FZI,FZJ ! Построить графически эпюры
!* Задать таблицу значений: моменты вдоль OX в глобальной системе координат
ETABLE,MXI,SMISC,4
ETABLE,MXJ,SMISC,64
PLLS, MXI, MXJ ! Построить графически эпюры
!* Задать таблицу значений: моменты вдоль OY в глобальной системе координат
ETABLE,MYI,SMISC,5
ETABLE,MYJ,SMISC,65
PLLS,MYI,MYJ ! Построить графически эпюры
!* Задать таблицу значений: моменты вдоль OZ в глобальной системе координат
ETABLE,MZI,SMISC,6
ETABLE,MZJ,SMISC,66
PLLS,MZI,MZJ ! Построить графически эпюры
FINISH
Для того чтобы получить значения реакций в закрепленных узлах, необходимо выполнить Main Menu > General Postproc > List Results > Reaction Solu. В меню List Reaction Solution выбрать OK. Результатом выполнения будет таблица значений реакций в зависимости от номера узла. Вывести конструкцию на экран, содержащую номера узлов, можно с помощью команд:
/PNUM,NODE,1
/REPLOT
Задание.
Используя данные эпюры максимальных напряжений, подобрать размеры сечения из условия прочности по допускаемым напряжениям: первый материал [σ] = 400 МПа, второй материал [σ] = 270 МПа.
4.5. УСТОЙЧИВОСТЬ ПЛОСКОЙ КОНСТРУКЦИИ.
Дана плоская рама. Материал – сталь, часть рамы имеет кольцевое сечение, часть – круговое сечение. Необходимо найти критическую нагрузку и рассмотреть формы потери устойчивости.
Геометрические размеры:
L = 3 м, d1 = 5 см, d2 = 3 см, d = 3 см, R = 1 м, H = 10 м.
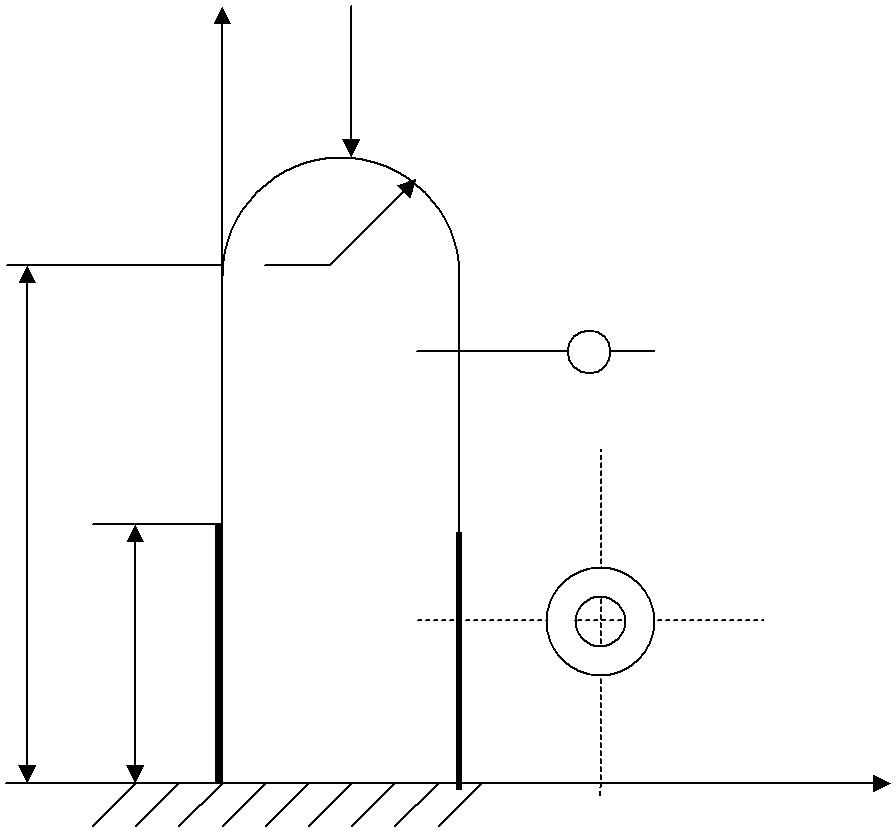
P
| d | ||
| H | d1, d2 | |
| l |
Для анализа задачи на устойчивость в линейной постановке необходимо:
1. Решить задачу статики с соответствующей единичной нагрузкой, при этом необходимо учитывать опции расчета предварительно напряженного состояния –
PRESTRESS.
2. Перейти в решение линейной задачи устойчивости и получить соответствующие критические нагрузки и формы устойчивости.
/PREP7
/UNITS,SI
PI=4*ATAN(1) ! Определим число Пи ! Геометрические параметры
L=3
R=1
H=10
! Геометрические параметры сечения d1=5e-2
d2=3e-2 d=3e-2
!* Задание ключевых точек
K,1,0,0,,
K,2,0,L,,
K,3,0,H,,
K,4,2*R,H,,
K,5,2*R,L,,
K,6,2*R,0,,
K,7,R,H,,
!* Построение дуги окружности
CIRCLE,7,R ! Построить полный круг с центром в точке 7
! Выделение нижнего полукруга
LSEL,S,RADIUS, ,R
LSEL,R,LOC,Y,H-R,H
! Удаление нижнего полукруга
LDELE,ALL
!* Построение линий
LSTR, 1, 2
LSTR, 2, 3
LSTR, 6, 5
LSTR, 5, 4
! Выделить все
ALLSEL, ALL
! Склеить линии для образования единой конструкции
LGLUE, ALL
!* Задание свойств материала
UIMP,1,EX, , ,2e11, ! Модуль Юнга UIMP,1,NUXY, , ,0.3, ! Коэффициент Пуассона
!* Задание типа элемента
ET,1,BEAM3
!* Задание опций элемента
KEYOPT,1,6,0
KEYOPT,1,9,9
KEYOPT,1,10,0
!* Задание констант элемента, первое сечение
! Номер констант, площадь сечения, момент инерции, высота сечения
R,1, PI*(D1**2-D2**2), PI*(D1**4-D2**4)/64, D1, , , ,
!* Задание констант элемента, второе сечение
R,2, PI*D**2/4, PI*D**4/64, D, , , ,
!* Задание атрибутов элемента, первое сечение
LSEL,S,LOC,Y,0,L ! Выделение линии
LATT,1,1,1 ! Присвоить атрибуты
LESIZE, ALL, , ,5,1, ! Число разбиений линии – 10, коэф. сжатия – 1 !* Задание атрибутов элемента, второе сечение
LSEL,S,LOC,Y,L,H+R ! Выделить линию
LATT,1,2,1 ! Присвоить атрибуты
LESIZE, ALL, , ,10,1, ! Число разбиений линии – 10, коэф. сжатия – 1 ALLSEL,ALL ! Выделить все
LMESH,ALL ! Построить сетку на всех линиях
! Закрепление узлов
! Выделить узел с координатами (0, 0) NSEL,S,LOC,X,0
NSEL,R,LOC,Y,0
! Закрепить узел – степени свободы UX,UY D,ALL, , , , , ,UX,UY
! Выделить узел с координатами (2*R, 0) NSEL,S,LOC,X,2*R
NSEL,R,LOC,Y,0
! Закрепить узел – степени свободы UX,UY D,ALL, , , , , ,UX,UY
! Выделить узел с координатами (R, H+R) NSEL,S,LOC,X,R
NSEL,R,LOC,Y,H+R
! Приложить единичную нагрузку
F,ALL,FY,-1, ALLSEL, ALL
FINISH ! Выход из препроцессора /SOLU ! Вход в процессор решения
PSTRES,ON ! Установить вычисление напряженного состояния SOLVE ! Запуск на решение
FINISH ! Выход из процессора /SOLU ! Вход в процессор решения
ANTYPE,1 ! Установить опции решения –
! анализ на устойчивость в линейной постановке
!* Определение метода решения и количества собственных форм,
! подлежащих определению
BUCOPT,SUBSP,4,0,4 ! Определить 4 формы MXPAND,4,0,0,0,0.001,
SOLVE ! Решение
FINISH ! Выход из процессора решения /POST1 ! Вход в постпроцессор
SET,FIRST ! Прочитать первый ряд расчетных значений PLDISP,1 ! Вывести деформированную форму графически
! Просмотреть следующую деформированную форму
SET,NEXT
PLDISP,1
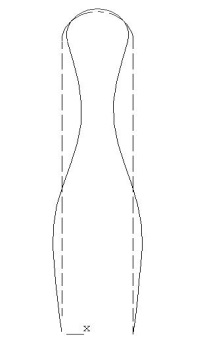
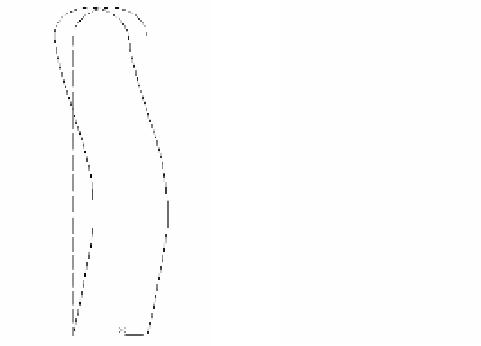
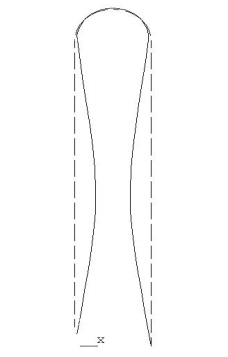
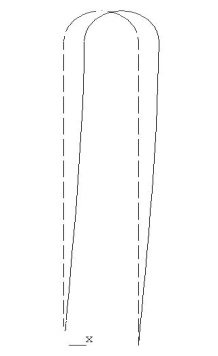
На данном этапе можно просмотреть значения критических сил. Для этого: Main Menu > General Postproc > Results Summary. В файле будут упорядоченные значения критических сил.
***** INDEX OF DATA SETS ON RESULTS FILE *****
| SET | TIME/FREQ | LOAD STEP | SUBSTEP | CUMULATIVE |
| 347.26 | ||||
| 2797.0 | ||||
| 3599.7 | ||||
| 9293.8 |
Задание.
Усилить конструкцию так, чтобы конструкция выдерживала двойную нагрузку, т.е. чтобы критическая нагрузка была бы 347.26*2.
4.6. ОПРЕДЕЛЕНИЕ СОБСТВЕННОЙ ЧАСТОТЫ ПРОСТЕЙШЕЙ МЕХАНИЧЕСКОЙ СИСТЕМЫ.
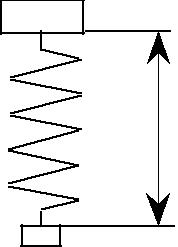
Определить собственную частоту системы пружина-масса. В данной задаче изучается принцип прямого конечно-элементного моделирования и спецификация решения для определения собственных частот.
C
| l |
M
Масса груза 10 кг, жесткость пружины 10 Н/м, длина 1 м.
Для моделирования данной системы применяется элемент пружины COMBIN14 и элемент точечной массы MASS21.
/PREP7
!*
C=10
M=10
L=1
ET,1,COMBIN14 ! Задание элемента пружины
!*
KEYOPT,1,2,0 ! Опции пружины – модель продольной деформации KEYOPT,1,3,2 ! Опции пружины – 2-х мерная пружина
!*
R,1,C, , , ! Коэффициент жесткости
!* Задание геометрических положений узлов
N,1,,,,,,,
N,2,,L,,,,,
E,1,2 ! Провести элемент через два узла
!*
ET,2,MASS21 ! Задание элемента массы
!*
KEYOPT,2,2,0 ! Опции – свойства задаются в глобальной системе координат KEYOPT,2,3,4 ! Опции – масса точечная
!*
R,2,M, ! Масса
!* Далее необходимо задать программе тип элемента и константы, !* которые будут действовать при задании элемента
TYPE, 2
REAL, 2
!* Задать элемент в узле 1 E, 1
!* Опции нумерации элементов
/PNUM,ELEM,1
/REPLOT EPLOT FINISH /SOLU
! Закрепление узлов
D,2, , , , , ,ALL, , , , ,
D,1, , , , , ,UX, , , , ,
!* Задание типа анализа – модальный анализ
ANTYPE,2
!*
MODOPT,SUBSP,1 ! Задание метода решения
EQSLV ,FRONT ! Определения типа решателя
MXPAND,1, , ,0 ! Число определяемых частот
!*
SUBOPT,8,4,6,0,0,ALL ! Опции для метода решения !*
OUTPR,BASIC,LAST, ! Управление выводом данных
!*
OUTRES,ALL,LAST, ! Управление записью данных в файл базы данных
SOLVE
FINISH
Для просмотра значений собственной частоты необходимо выполнить: Main Menu > General Postproc > Results Summary. Получим значение 0,15915.
Изучим возможности временного постпроцессора POST26, представления данных в виде массивов и вывода данных в файл. Файл с нижеследующим содержанием необходимо выполнять только в командном режиме.
/POST26 ! Вход во временной постпроцессор
! Получить значение первой собственной частоты и
! присвоить ее значение переменной FREQ *GET,FREQ,MODE,1,FREQ
! Создать массив для строковой переменной LABEL размерностью 1*2 *DIM,LABEL,CHAR,1,2
! Создать массив для действительной переменной VALUE размерностью 1*3 *DIM,VALUE,,1,3
! Присвоение значений переменной
LABEL(1,1) = ' F,'
LABEL(1,2) = ' (Hz) '
! Вычислить теоретическое значение собственной частоты
FreqTh=SQRT(C/M)/(8*ATAN(1))
! Заполнить массив данными
*VFILL,VALUE(1,1),DATA, FreqTh *VFILL,VALUE(1,2),DATA, FREQ *VFILL,VALUE(1,3),DATA, (FreqTh-FREQ)*100/FREQ
! Задать файл MODE.txt, в который напечатаны значения
/OUT, MODE,txt
! Следующие значения будут содержать комментарии в файле
/COM
/COM,_________________________ RESULTS ___________________________
/COM,
/COM, | THEORY | ANSYS | Eps (%)
/COM,
! *VWRITE – это оператор печати в файл, следующая за ним строка
! содержит формат вывода данных. Синтаксис форматного вывода аналогичен
! оператору FORMAT в FORTRAN *VWRITE,LABEL(1,1),LABEL(1,2),VALUE(1,1),VALUE(1,2),VALUE(1,3) (1X,A8,A8,' ',F18.14,' ',F18.14,' ',F5.3) /COM,_____________________________________________________________
/OUT FINISH
Результат выполнения программы будет в файле MODE,txt в следующем виде:
____________________________ RESULTS ___________________________
| THEORY | ANSYS | Eps (%)
F, (Hz) 0.15915494309190 0.15915494309190 0.000
____________________________________________________________________
Замечание.
В ANSYS выдается значение не круговой частоты ω, а обычной частоты ν = 2ωπ . Из решения
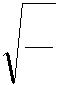
| данной задачи следует, что ω = | c | =1 , | ν = | = 0,15915 . | ||
| m | 2π | |||||
Задание.
Определить частоты колебаний системы с двумя степенями свободы.
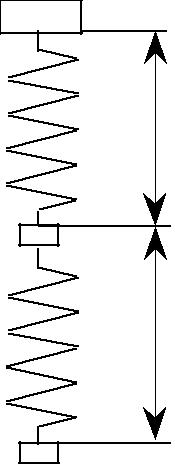
| l1 |
m1
| l2 |
M2
c1
c2
4.7. ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ЧАСТОТ ПЛОСКОЙ РАМЫ.
Дана плоская рамная конструкция. Найти собственные формы и собственные частоты конструкции.
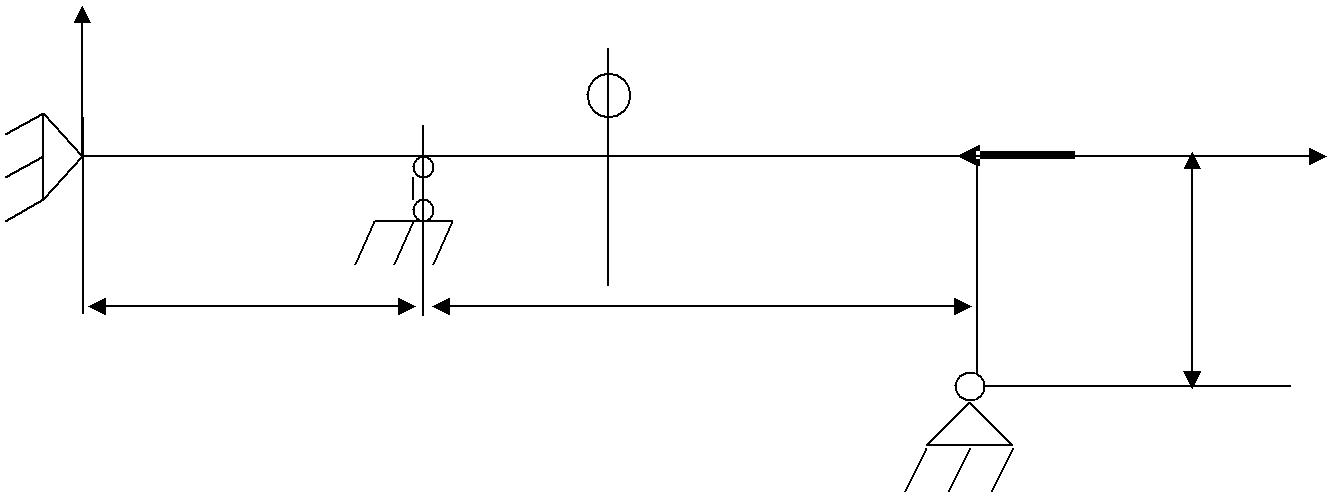
| d | P | |||
| a | b | c | ||
Рама сделана из стали, поперечное сечение – круг диаметром 2 см. Геометрические параметры: а = 1 м, b = 1.5 м, с = 0.5 м. Приложенная сила Р = 1000 Н.
/PREP7
/UNITS,SI
PI=4*ATAN(1) ! Определим число Пи
! Геометрические параметры рамы a=1
b=1.5
c=0.5
! Диаметр сечения
d=1e-2
! Сила
P=1000
! ********
!* Построение точек
K,1,0,0,,
K,2,a,0,,
K,3,a+b,0,,
K,4,a+b,-c,,
!* Построение линий
LSTR, 1, 2
LSTR, 2, 3
LSTR, 3, 4 ALLSEL, ALL
!* Задаем тип элемента
ET,1,BEAM3
! Задание опций элемента
KEYOPT,1,6,0
KEYOPT,1,9,9
KEYOPT,1,10,0
! Задание констант элемента
R,1, PI*D**2/4, PI*D**4/64,D, , , ,
! Свойства материала
UIMP,1,EX, , ,2e11, ! Модуль Юнга UIMP,1,DENS, , ,7800, ! Плотность материала UIMP,1,NUXY, , ,0.3, ! Коэффициент Пуассона
!* Построение сетки
LESIZE, ALL, , , 10, 1, ! Задание числа разбиений LMESH,ALL ! Построение сетки
!* Задаем условия закрепления узлов
NSEL,S,LOC,X,0
NSEL,R,LOC,Y,0 D,ALL, , , , , , ,UX, UY
!
NSEL,S,LOC,X,A
NSEL,R,LOC,Y,0
D,ALL, , , , , , ,UY
!
NSEL,S,LOC,X,A+B
NSEL,R,LOC,Y,-C
D,ALL, , , , , ,UX,UY !* Задание силы
NSEL,S,LOC,X,A+B
NSEL,R,LOC,Y,0 F,ALL,FX,-P,
!
ALLSEL, ALL
!
/SOLU
!* Анализ на собственные частоты
ANTYPE,2
!*
MODOPT,SUBSP,4 ! Спецификация метода решения и количества частот
EQSLV,FRONT ! Тип решателя
MXPAND,4, , ,0 ! Записывать решения 4 собственных форм
!* SOLVE FINISH
Результаты постпроцессорной обработки.
Лист со значениями собственных частот доступен через следующее меню: Main Menu > General Postproc > Results Summary.
***** INDEX OF DATA SETS ON RESULTS FILE *****
| SET | TIME/FREQ | LOAD STEP | SUBSTEP | CUMULATIVE |
| 13.650 | ||||
| 25.607 | ||||
| 44.718 | ||||
| 79.535 |
Первая форма колебаний. /POST1
SET,FIRST
PLDISP,1
Следующая форма колебаний. SET,NEXT
PLDISP,1
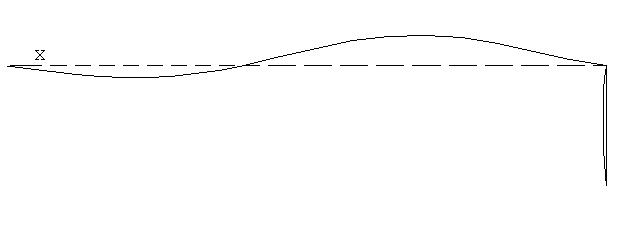

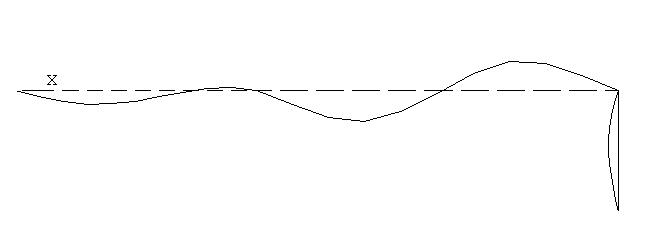
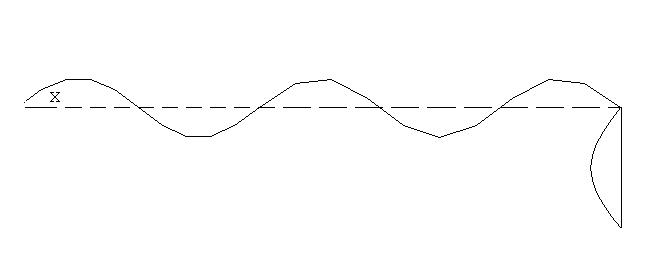
Форму колебаний можно анимировать. Utility Menu > PlotCtrls > Animate > Mode Shape. OK. Далее последует операция создания видео файла формата .avi, который можно просматривать стандартными средствами Windows.
4.8. ОПРЕДЕЛЕНИЕ ДИНАМИЧЕСКОГО ОТКЛИКА ПРИ ВНЕЗАПНОМ ПРИЛОЖЕНИИ НАГРУЗКИ НА ПЛОСКУЮ РАМУ.
Плоскую рамную конструкцию рассмотрим из предыдущего примера. Система покоится и в начальный момент прикладывается сила P. Найти динамическую реакцию на внезапное приложение нагрузки.
Данные предыдущего анализа на собственные частоты используются для динамического анализа для определения характерного времени динамической реакции. Поскольку в ANSYS реализована устойчивая схема интегрирования Ньюмарка, то для определения характерного времени можно взять время, равное собственному периоду, например, в данном примере 1/13.650 = 0.07326.
Блок создания геометрии будет точно такой же, как и в предыдущем примере.
/PREP7
/UNITS,SI
PI=4*ATAN(1) ! Определим число Пи
! Геометрические параметры рамы a=1
b=1.5
c=0.5
! Диаметр сечения
d=1e-2
! Сила
P=1000
! Параметры времени
T=0.07326
! ********
!* Построение точек
K,1,0,0,,
K,2,a,0,,
K,3,a+b,0,,
K,4,a+b,-c,,
!* Построение линий
LSTR, 1, 2
LSTR, 2, 3
LSTR, 3, 4 ALLSEL, ALL
!* Задаем тип элемента
ET,1,BEAM3
! Задание опций элемента
KEYOPT,1,6,0
KEYOPT,1,9,9
KEYOPT,1,10,0
! Задание констант элемента
R,1, PI*D**2/4, PI*D**4/64,D, , , ,
! Свойства материала
UIMP,1,EX, , ,2e11, ! Модуль Юнга UIMP,1,DENS, , ,7800, ! Плотность материала UIMP,1,NUXY, , ,0.3, ! Коэффициент Пуассона
!* Построение сетки
LESIZE, ALL, , , 10, 1, ! Задание числа разбиений LMESH,ALL ! Построение сетки
!* Задаем условия закрепления узлов
NSEL,S,LOC,X,0
NSEL,R,LOC,Y,0 D,ALL, , , , , , ,UX, UY
!
NSEL,S,LOC,X,A
NSEL,R,LOC,Y,0
D,ALL, , , , , , ,UY
!
NSEL,S,LOC,X,A+B
NSEL,R,LOC,Y,-C
D,ALL, , , , , ,UX,UY !* Задание силы
NSEL,S,LOC,X,A+B
NSEL,R,LOC,Y,0 F,ALL,FX,-P,
!
ALLSEL, ALL
! Блок решения для динамической задачи /SOLU ! Вход в процессор решения
ANTYPE,4 ! Спецификация решения – нестационарный анализ !* Печатать в файл данные анализа каждый шаг
OUTPR,BASIC,ALL,
!* Печатать в файл основные величины анализа
OUTRES,ALL,ALL,
TIME, T ! Конечное время интегрирования
AUTOTS,0 ! Автоматический выбор шага интегрирования выключен
! Шаг интегрирования задаем самостоятельно T/100
DELTIM,T/100, , ,1
KBC,1 ! Нагрузка от шага к шагу прикладывается ступенчато
! Задание начальных условий
IC,ALL,ALL,0,0,
! ко всем узлам (ALL), на все степени свободы (ALL) –
! начальные перемещения u0 = 0,
! начальная скорость v0 = 0
SOLVE ! Запуск на решение
FINISH
Для анализа результатов можно использовать как постпроцессор POST1, так и POST26. Постпроцессор POST26 позволяет строить графики вида u = u (t).
Постпроцессор POST1 – построение пошагового результата и анимация.
! Построение графика Uy(t) для узла с координатами (A+B, 0) /POST26
! Выделить узел с координатами (A+B, 0) NSEL,S,LOC,X,A+B
NSEL,R,LOC,Y,0
! Переменной ND присвоить номер узла
*GET, ND, NODE, , NUM, MAX
! Создать файл значений для узла с номером ND,
! получаемая переменная имеет номер 2 и имя UY
! U, Y – перемещения вдоль оси OY NSOL,2,ND,U,Y,UY
!*
PLVAR,2, , , , , , , , , , ! Построить график FINISH
Задание.
Изучить влияние густоты сетки и шага интегрирования на результат решения задачи.
[3] Построение матриц жесткости при выполнении учебных заданий по методу конечных элементов может быть выполнено с помощью входящей в состав настоящего учебника программы “Библиотека плоских стержневых конечных элементов”, разработанной кафедрой строительной механики и теории упругости СПбГТУ.
Дата добавления: 2015-12-16; просмотров: 995;
