Классификация математических моделей 3 страница

Легко увидеть, что каждый столбец этой матрицы состоит из усилий, действующих на узлы элемента при единичном смещении по направлению какой-либо из его степеней свободы при условии, что перемещения по направлению остальных степеней свободы равны нулю.

Например, первый столбец представляет собой усилия, действующие на узлы элемента при единичном смещении узла 1 (4-ый индекс при коэффициентах) по направлению 1 (2-ой индекс при коэффициентах) при условии, что перемещения по направлению остальных степеней свободы равны нулю. Второй столбец представляет собой усилия, действующие на узлы элемента при единичном смещении узла 1 (4-ый индекс при коэффициентах) по направлению 2 (2-ой индекс при коэффициентах) при условии, что перемещения по направлению остальных степеней свободы равны нулю (рис.13). И так далее.

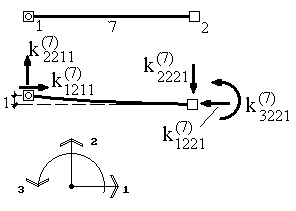Рис. 13

Докажем, что это действительно так, например, для первого стобца матрицы жесткости.

Зададим перемещение узла 1 по направлению 1 элемента равным 1, в то время как все его остальные узловые перемещения будем считать равными нулю. В этом случае вектор узловых перемещений приобретает вид:

,

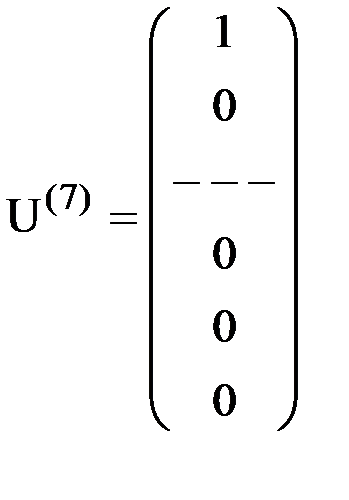и равенство (2) становится следующим:

.

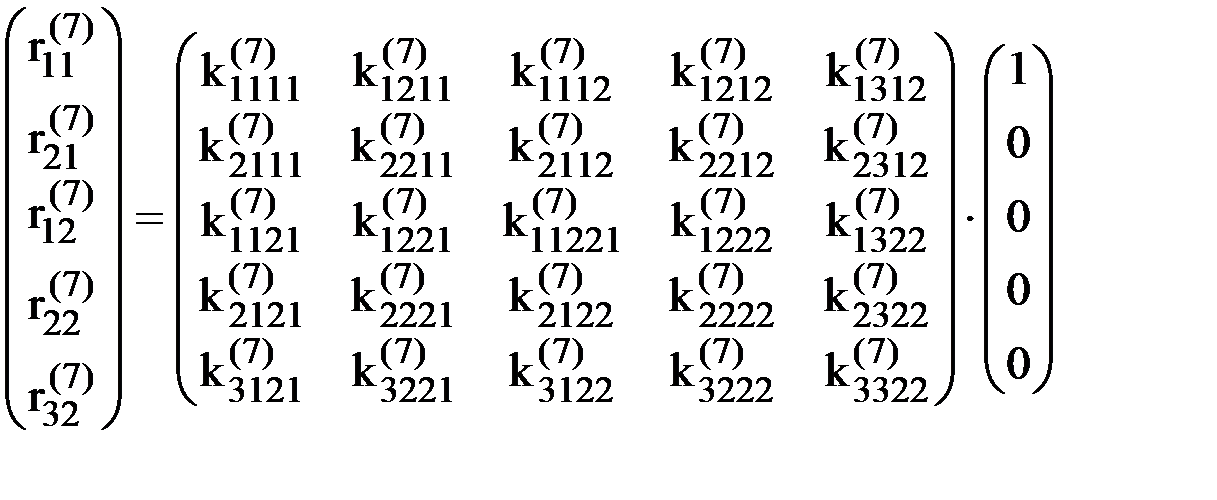Отсюда:

,

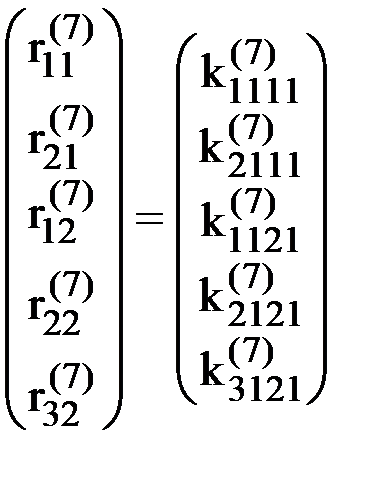т.е. компоненты первого столбца матрицы жесткости на самом деле оказались равными компонентам вектора усилий, действующих на узлы элемента при заданном смещении.

Придавая соответствующий вид вектору узловых перемещений, можно выполнить аналогичное доказательство для любого другого столбца матрицы жесткости элемента.

Для рассматриваемого элемента (рис.9) запишем матричное равенство (2) в развернутом виде:

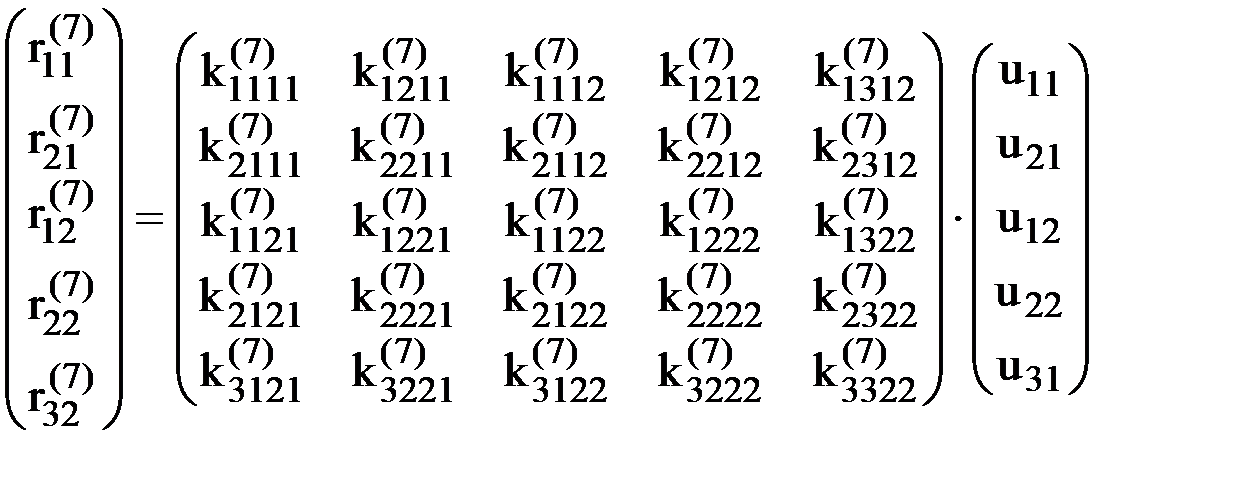
или:

.

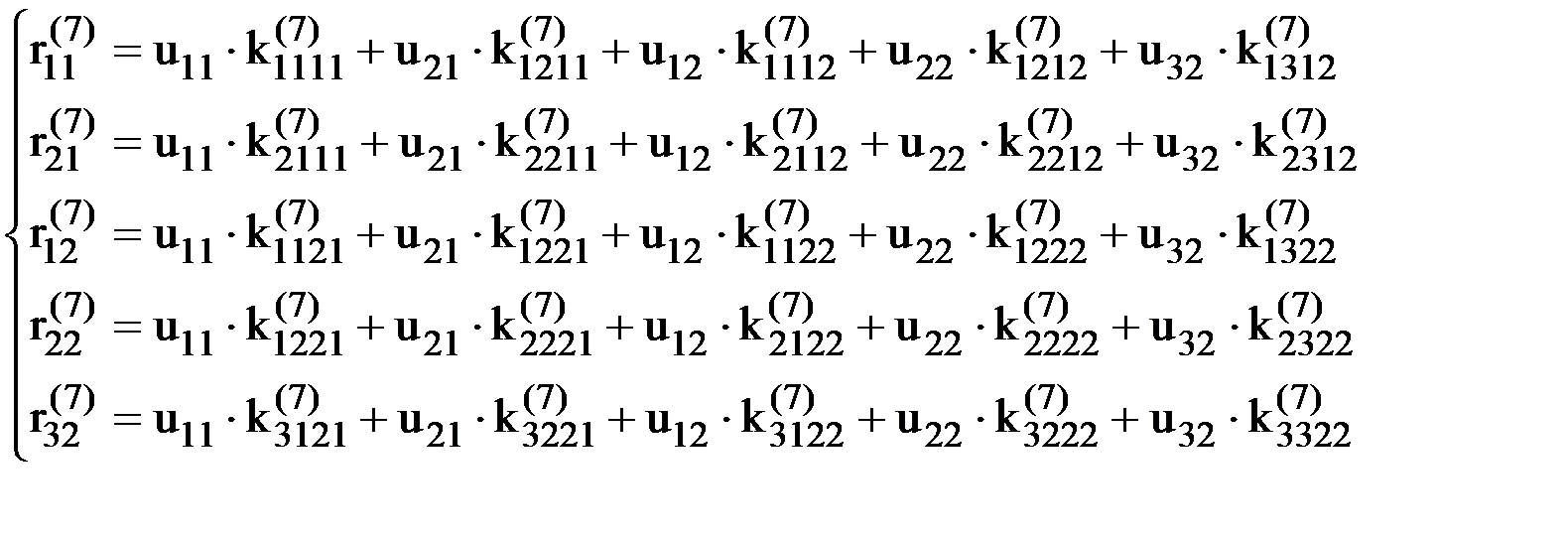Физический смысл любого из уравнений данной системы очевиден.

Если узел k элемента е получает по направлению j единичное перемещение, то усилие, действующее при этом на узел m по направлению i равно 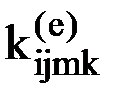. Если же это перемещение будет равно не единице, а 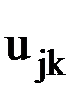, то в соответствии с линейным законом связи между усилиями и перемещениями, рассматриваемое усилие увеличится также в 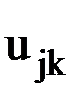раз и составит .

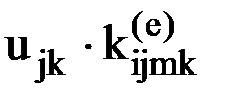Пусть теперь все узлы элемента получают смещения по направлению всех имеющихся у элемента степеней свобод. Тогда, в соответствии с принципом суперпозиций, усилие 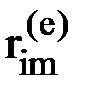, т.е. усилие, действующее на какой- либо узел m по какому-либо направлению i, будет представлять собой сумму усилий, вызванных смещениями всех узлов элемента по направлению всех имеющихся степеней свобод (рис.14). Поскольку, как мы только что выяснили, при перемещении какого-либо узла k по направлению j на величину 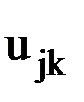на узел m по направлению i будет действовать усилие 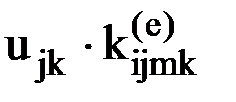, суммарное усилие, действующее на узел m по направлению j, будет представлять собой сумму величин 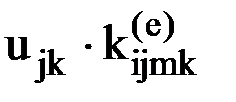для всех степеней свободы элемента (рис.14).

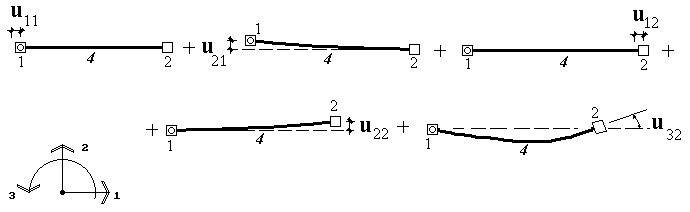Рис. 14

Формально это можно записать следующим образом:

,

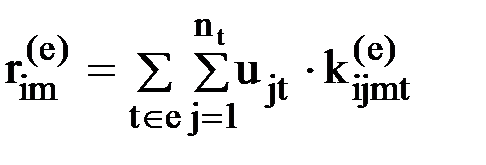(3)

где t- номер узла, входящего в элемент е, запись 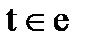означает, что суммирование производится по всем узлам, входящим в элемент е, n_t - число степеней свободы в узле t. Причем, n_t=2, если узел t - шарнирный, и n_t=3, если узел t жесткий.

Как мы уже выяснили, элементы, стоящие на главной диагонали матрицы жесткости элемента должны быть положительными. Кроме того, матрица жесткости элемента должна быть симметричной. Действительно, в соответствии с теоремой взаимности реакций, усилие, действующее на узел m по направлению i, от единичного перемещения узла k этого же элемента по направлению j должно равняться усилию, действующему на узел k по направлению j, от единичного перемещения узла m этого же элемента по направлению i, т.е. .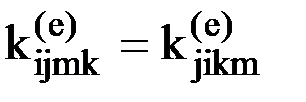

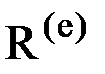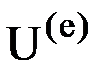Аналогично векторам и матрица жесткости элемента K^(e) также является блочной. Она состоит из блоков 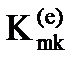, каждый из которых содержит коэффициенты, связывающие перемещения k-го узла элемента и реакции, возникающие при этом, в m-ом узле данного элемента.

Например, для рассматриваемого элемента (рис.9):

.

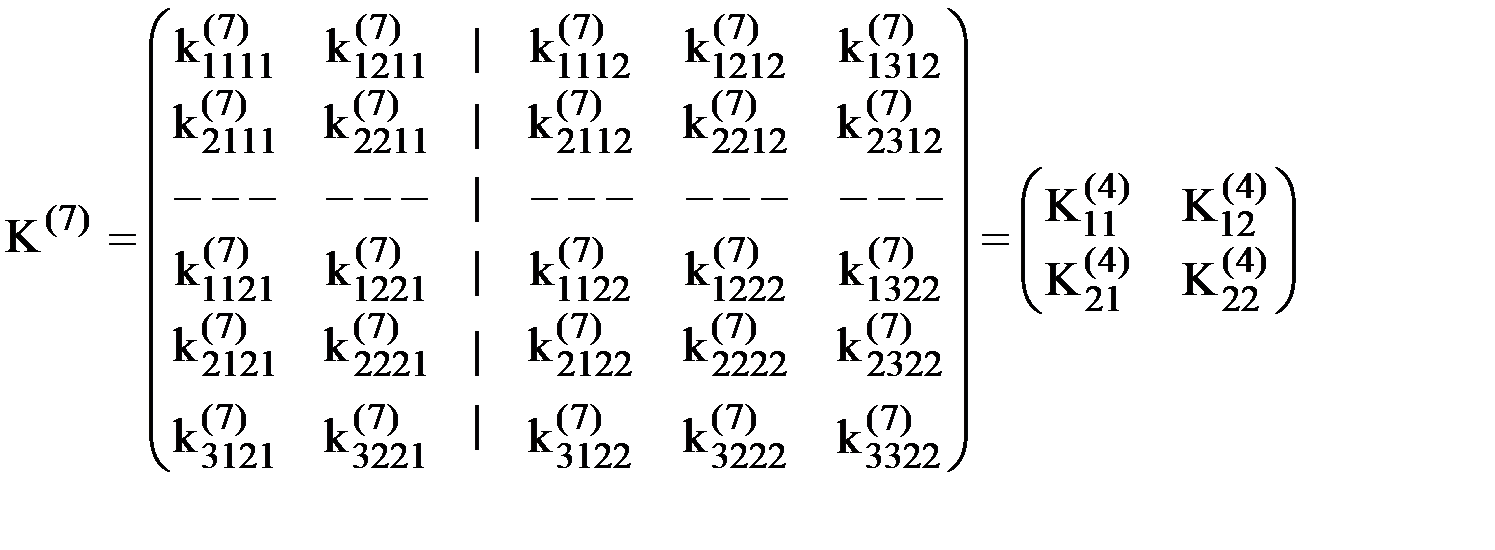Преобразование матрицы жесткости при переходе от одной системы координат к другой.

Обычно матрицу жесткости строят в удобной для данного элемента системе координат, которую принято называть локальной или местной. При переходе от отдельных элементов к системе элементов необходимо осуществить переход от локальных систем координат к общей для всех элементов системе координат, которую принято называть глобальной.

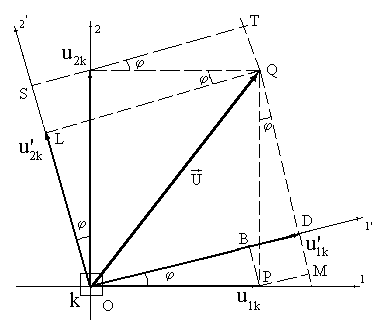Рис. 15

Пусть известны перемещения какого-либо жесткого узла k элемента в локальной системе координат, оси которой 1` и 2` повернуты на угол j относительно осей 1 и 2 глобальной системы координат. Оси 3 и 3`, очевидно, будут совпадать, т.к. в обоих случаях рассматривается одна и та же плоскость (рис.15). 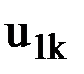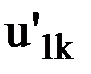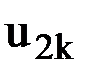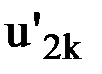Пусть и - перемещения узла k по направлению 1 в глобальной и локальной системах координат соответственно, а и - перемещения по направлению 2 в глобальной и локальной системах координат соответственно.

Из рис.15 следует:

,

.

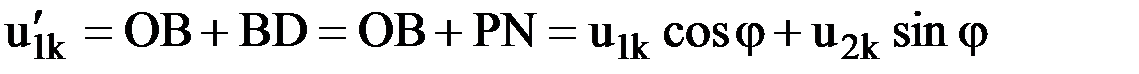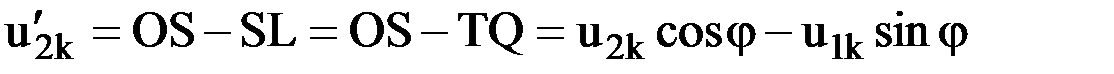Очевидно, угловое смещение в обоих системах осей координат будет одинаковым, т.е. 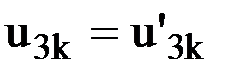. Полученные соотношения, связывающие перемещения узла в локальной и в глобальной системах координат, в матричной форме будут выглядеть следующим образом:

.

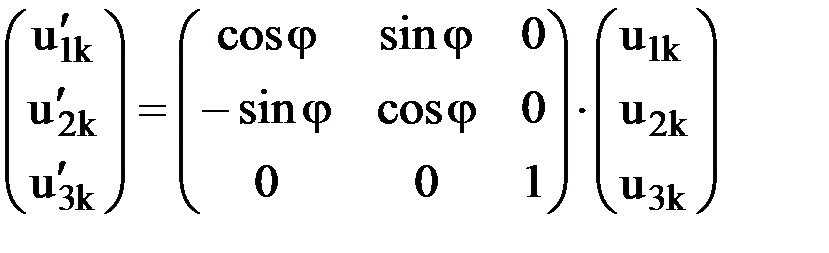Матрица 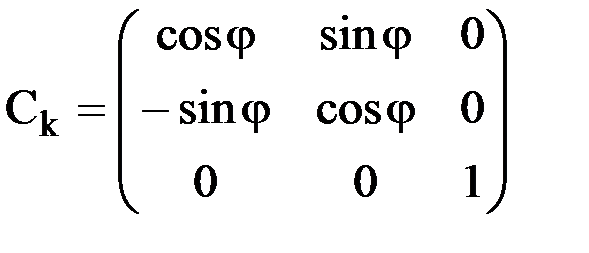называется матрицей направляющих косинусов для k-го узла. Легко убедиться, что элемент, стоящий в ее i-ой строке и j-ом столбце равен косинусу угла между i-ой осью в локальной системе координат и j-ой осью в глобальной системе координат.

Для шарнирного элемента связь между перемещениями в локальной и глобальной системах осей будет аналогичной:

.

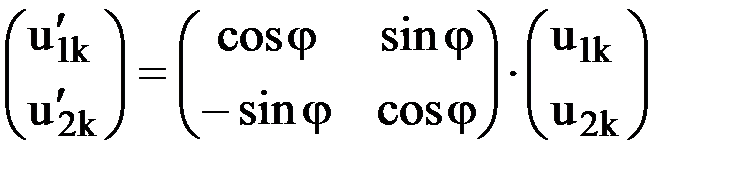Для элемента, содержащего несколько узлов, связь между вектором узловых перемещений U в глобальной системе осей координат и вектором узловых перемещений U` в локальной системе осей координат осуществляется при помощи квазидиагональной матрицы направляющих косинусов C^(e) элемента, составленной из матриц направляющих косинусов входящих в элемент узлов:

.

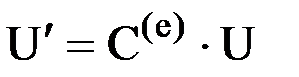(4)

Например, для элемента, изображенного на рис.9, выражение (4) будет выглядеть следующим образом:

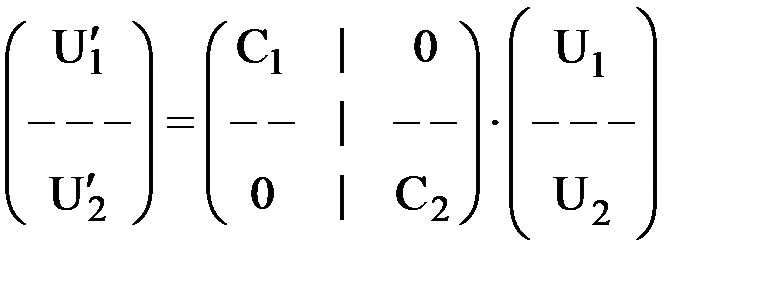
или

.

Легко убедиться, что это равенство соответствует уравнениям, связывающим перемещения в локальной и глобальной системах осей координат:

,

,

,

,

.

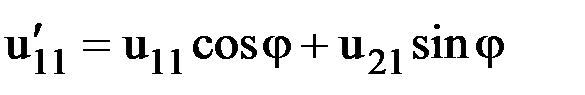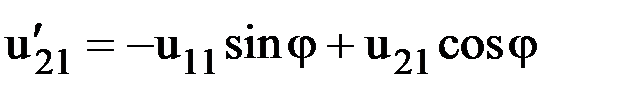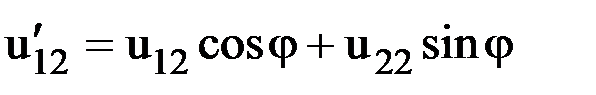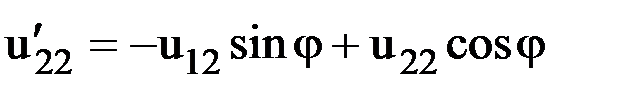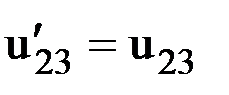Повторив те же рассуждения для усилий, действующих на узлы элемента, получим аналогичную (4) зависимость между векторами усилий, действующих на элемент, построенных для глобальной системы координат R^(e) и для локальной системы координат R`^(e):

.

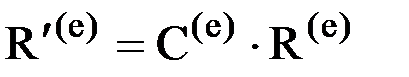(5)

Усилия, действующие на узлы элемента и узловые перемещения связаны зависимостью (2). Запишем ее также и для локальной системы осей координат:

.

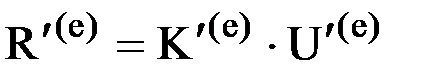(6)

Заменим в (6) вектора усилий и перемещений согласно зависимостям (4) и (5): 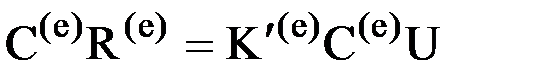и умножим получившееся равенство слева на матрицу 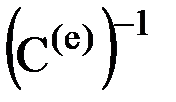, т.е. на матрицу, обратную матрице направляющих косинусов элемента: 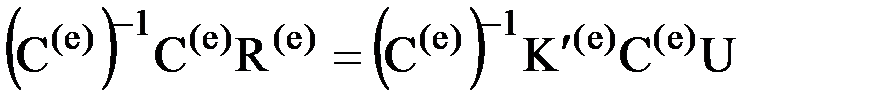. Сопоставляя это выражение с (2), получим зависимость, связывающую матрицы жесткости, построенные в глобальной и локальной системах координатных осей: 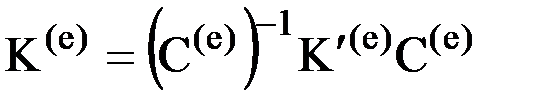. Известно, что у матрицы направляющих косинусов С^(е) обратная матрица совпадает с транспонированной матрицей. Поэтому, окончательно получаем:

.

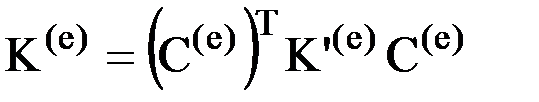(7)

Итак, если матрица жесткости элемента построена в локальной системе осей координат, то по формуле (7) можно получить из нее матрицу жесткости элемента в глобальной системе осей координат.

Примеры построения матрицы жесткости элемента.

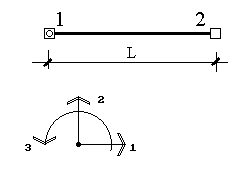Рис. 16

Построим матрицу жесткости элемента на рис. 16. Пусть L - длина элемента, EF - жесткость стержня на растяжение-сжатие, EI - жесткость стержня на изгиб.

Рассматриваемый элемент имеет 5 степеней свободы - две степени свободы в узле 1 и три в узле 2. Соответственно, матрица жесткости элемента имеет размер 5´5 и блочную структуру:

.

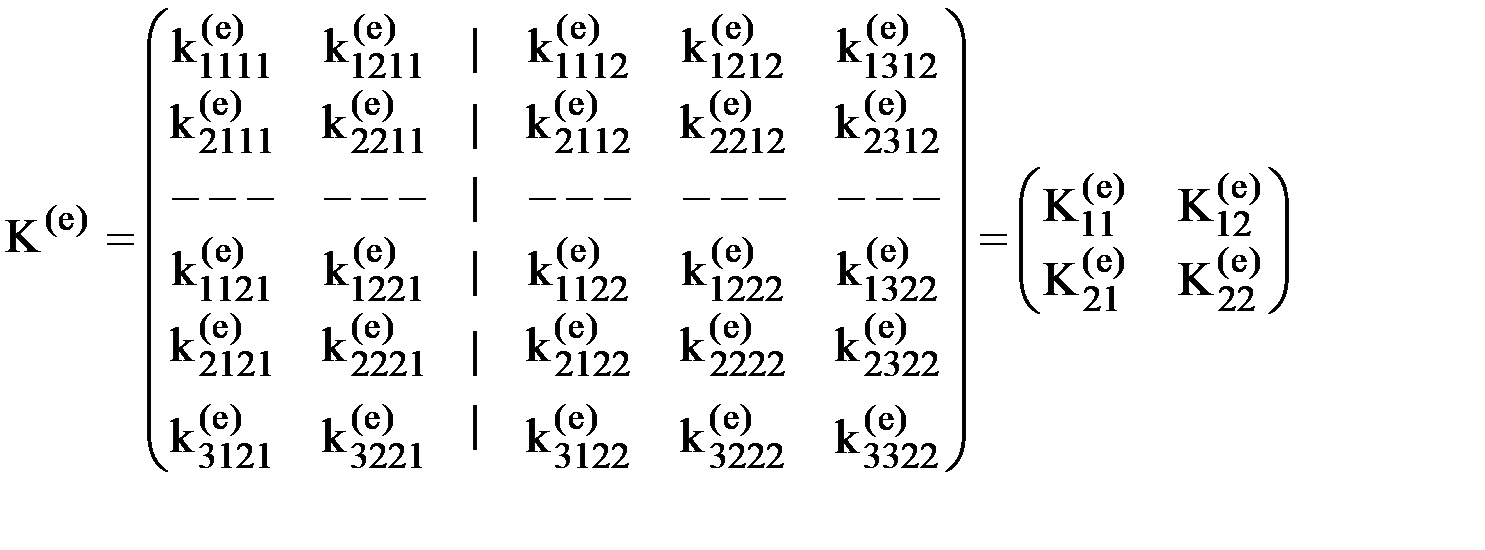Как известно, каждый столбец матрицы жесткости элемента представляет собой усилия, действующие на элемент в узлах при единичном смещении по направлению какой-либо степени свободы. Поэтому, для построения любого столбца матрицы жесткости элемента следует задать единичное смещение по направлению соответствующей степени свободы элемента и найти усилия, действующие при этом на его узлы. Выполнив последовательно эту операцию для всех степеней свободы элемента, по столбцам построим всю матрицу жесткости элемента.

Закрепим от смещения все узлы рассматриваемого элемента (рис.17). Тогда, задавая единичное смещение в одной из опорных связей, наложенных на полученную систему, мы обеспечим отсутствие перемещений по направлению остальных связей. Реакции в опорах при этом будут представлять собой искомые усилия.

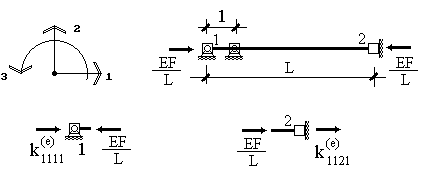Рис. 18

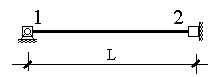Рис. 17

Первый столбец матрицы жесткости рассматриваемого элемента представляет собой усилия в узлах элемента при единичном смещении узла 1 по направлению 1. При этом на элемент со стороны опорных связей будут действовать только усилия по направлению 1 (рис.18), вызывающие его сжатие, причем усилие в узле 1 совпадает по направлению с осью 1, а в узле 2 оно направлено в обратную сторону. Величина этого усилия будет равна 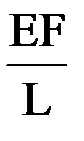. Действительно, продольное усилие N, возникающее в стержне при его растяжении или сжатии, связано с продольной деформацией (относительным удлинением) 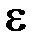посредством закона Гука: 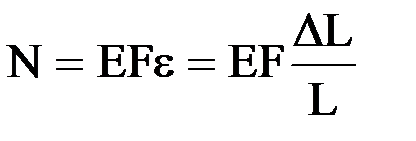. При 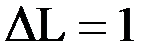отсюда имеем 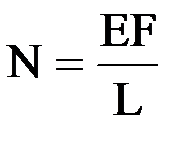. Таким образом, с учетом знака элементы первого столбца матрицы жесткости элемента будут равны:

.

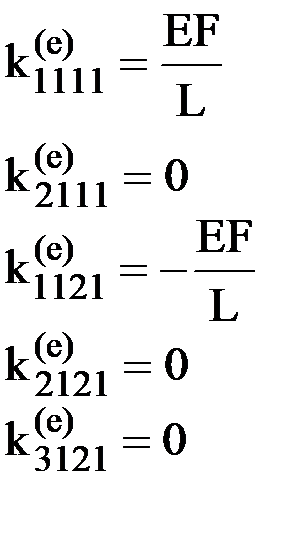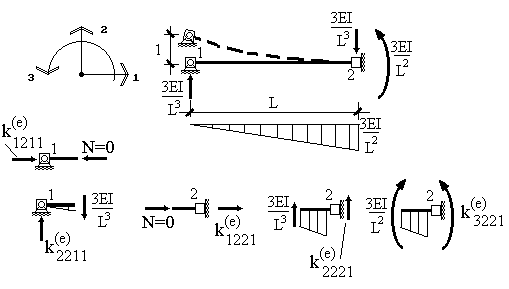Рис. 19

Для построения второго столбца зададим единичное смещение в узле 1 по направлению 2 (рис.19). Для данной задачи существует известное табличное решение (см.табл.11.1), на основании которого путем рассмотрения равновесия вырезанных из элемента узлов (рис.19) определяются элементы второго столбца матрицы жесткости элемента:

.

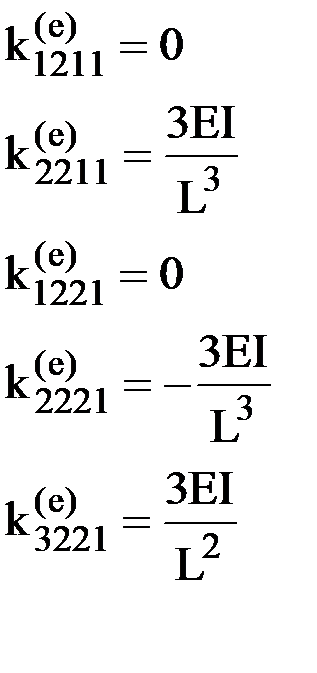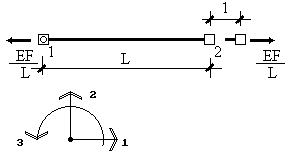Рис. 20

Теперь зададим единичное смещение узла 2 по направлению 1 (рис.20) и построим третий столбец матрицы жесткости элемента. В этом состоянии элемент будет испытывать продольное растяжение. Повторяя рассуждения аналогичные сделанным при построении первого столбца матрицы жесткости, получим:

.

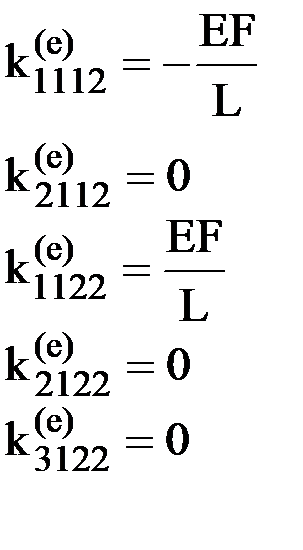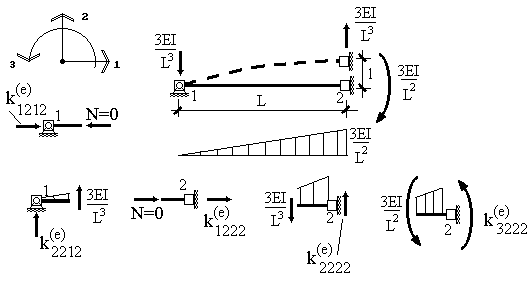Рис. 21

Для построения четвертого столбца матрицы жесткости зададим единичное смещение узла 2 по направлению 2 (рис.21):

.

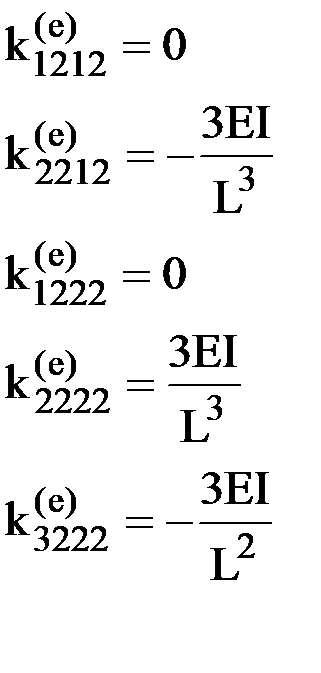И наконец, для построения пятого столбца матрицы жесткости зададим единичное смещение узла 2 по направлению 3 (рис.22):

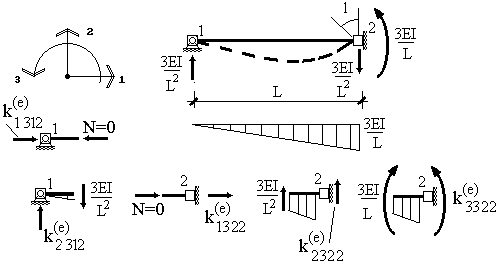Рис. 22

.

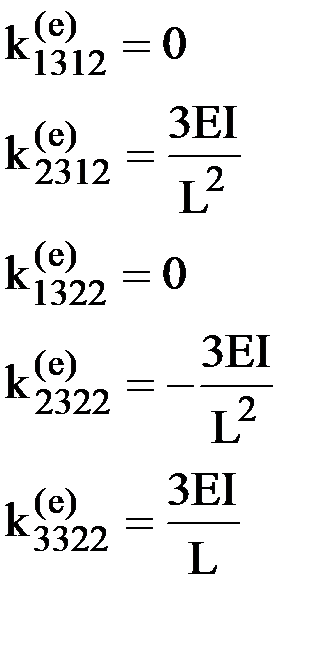Итак, матрица жесткости рассматриваемого элемента принимает вид:

.

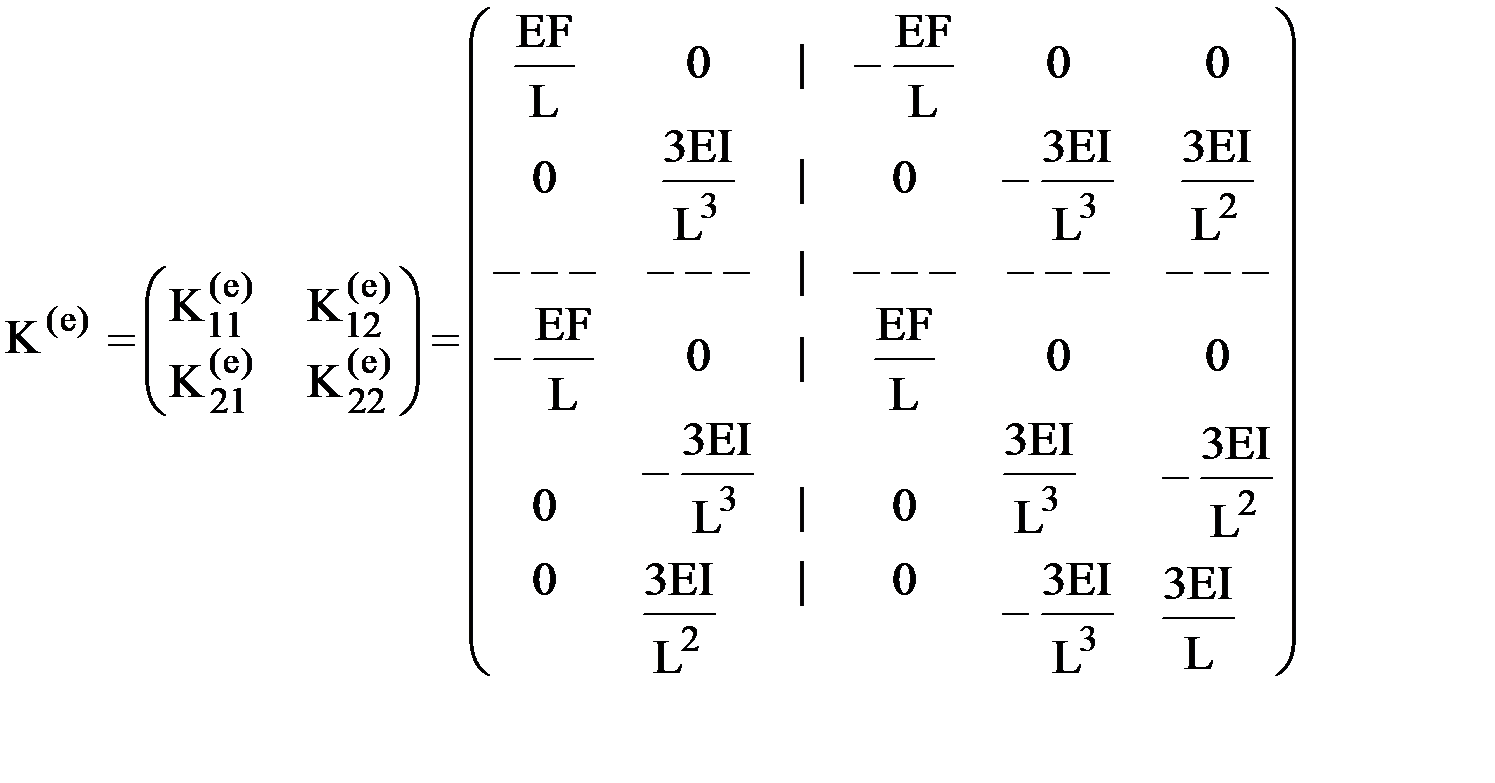Как и следовало ожидать, построенная матрица оказалась симметричной, а элементы, стоящие на ее главной диагонали, оказались положительными. Проверка выполнения этих условий - одно из средств контроля правильности построения матрицы жесткости.

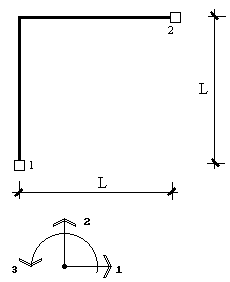Рис. 23

Рассмотрим теперь Г-образный элемент (рис.23). Будем считать, что жесткости обоих стержней элемента равны. Ограничимся построением для него только пятого столбца матрицы жесткости, предоставив построение остальных столбцов читателю.

В данном элементе два жестких узла, следовательно, элемент имеет шесть степеней свободы, а матрица жесткости элемента имеет следующую блочную структуру:

.

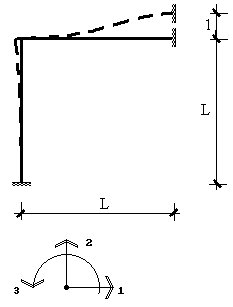Рис. 24

Элементы интересующего нас пятого столбца матрицы жесткости представляют собой усилия, действующие на узлы элемента при единичном смещении узла 2 по направлению 2. Для их определения нужно найти опорные реакции в стержневой системе, полученной при наложении связей по напрвлению всех степеней свободы элемента (рис.24), при единичном смещении ее верхней опоры по направлению 2.

Данная задача три раза статически неопределима ( 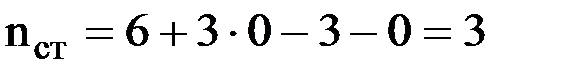) и один раз кинематически неопределима ( 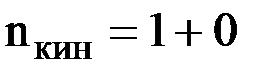), следовательно, для ее решения выгоднее использовать метод перемещений. При этом, как обычно в методе перемещений, будем пренебрегать продольными деформациями стержней по сравнению с их изгибными деформациями.

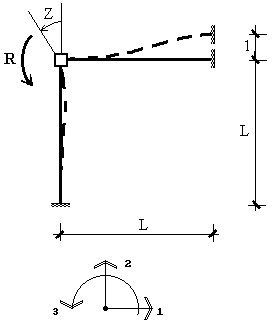Рис. 25

Основную систему метода перемещений образуем введением в жесткий узел связи, препятствующей его повороту. Потребовав, чтобы при повороте этого узла на величину Z реакция R во введенной связи равнялась нулю, получим задачу эквивалентную исходной (рис.25).

Далее построим основное и вспомогательное состояния основной системы (рис.26). Из равновесия узла (рис.26) находим реакции во введенной связи в основном и вспомогательном состояниях: 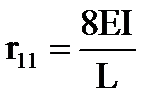, 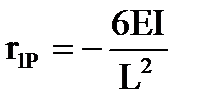. Из уравнения, выражающего условие отсутствия реакции во введенной связи в эквивалентной задаче 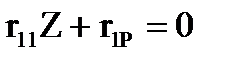, находим: .

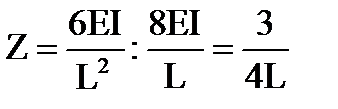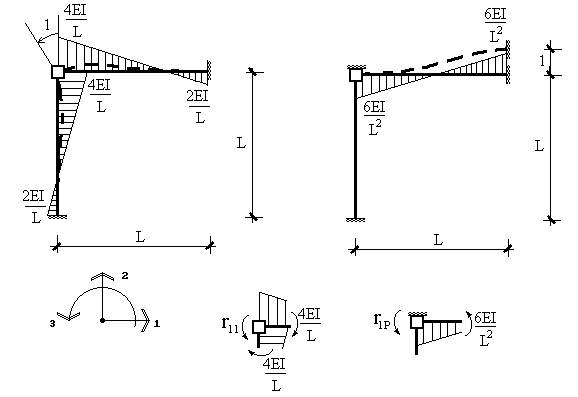Рис. 26

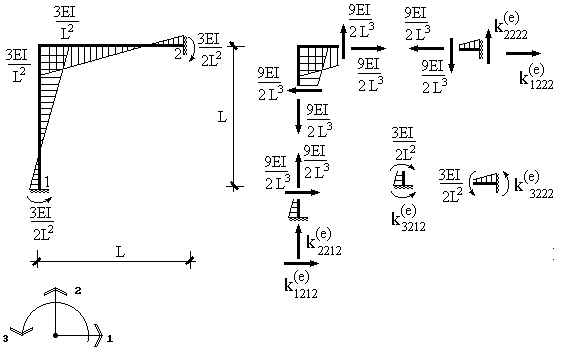Рис. 27

Найдя лишнее неизвестное, можем построить окончательную эпюру моментов (рис.27), пользуясь формулой 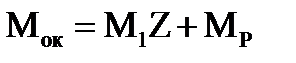. По построенной эпюре моментов путем вырезания узлов легко определить действующие в стержнях продольные и поперечные силы, а по ним и реакции в опорах (рис.27). Таким образом, по реакциям в опорах определяются элементы искомого столбца матрицы жесткости:

.

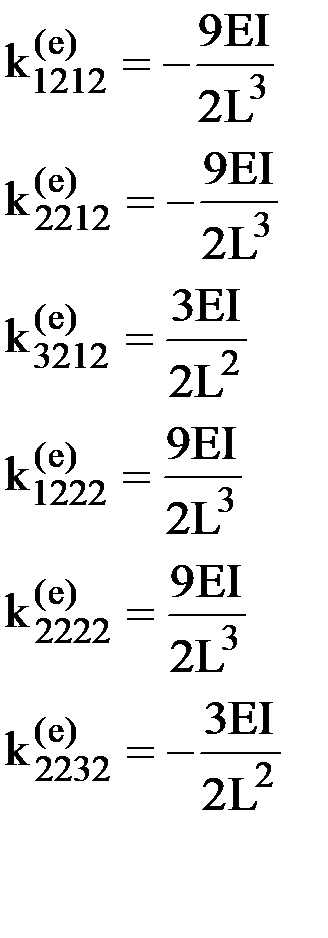Важно иметь в виду, что продольные деформации в стержнях при определении этих значений не учитывались, поэтому использование построенной подобным образом матрицы жесткости элемента в расчетах будет приводить к погрешностям в решении. В элементах, представляющих собой один стержень (рис.4), учет продольных деформаций проблем не вызывает. Поэтому использование в конечно-элементной схеме только таких элементов позволит получить точное решение задачи, если не учитывать погрешностей округления.

Формирование и решение системы уравнений МКЭ. Определение внутренних усилий в элементах.

Обозначим 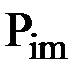-внешнее усилие, приложенное к узлу m и действующее по направлению i. Введем для каждого из n узлов конечно-элементной схемы вектор внешних узловых усилий, приложенных к узлу m. Если узел m - жесткий, то 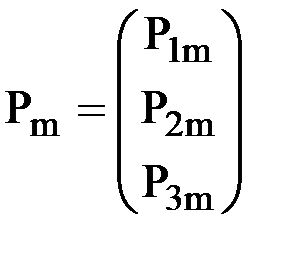, если шарнирный, то .

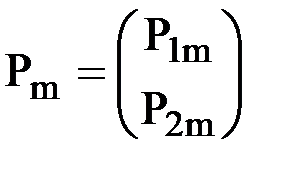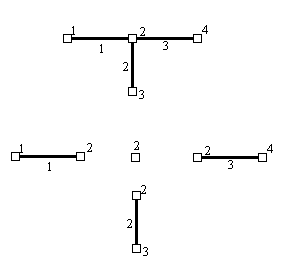Рис. 28

Рассмотрим равновесие любого свободного узла (т.е. такого узла, на перемещения которого не наложены связи) конечно-элементной сетки. Пусть это будет узел под номером 2 конечно-элементной сетки, изображенной на рис.28. Будем считать пока, что все узлы этой сетки свободны, т.е. на узлы не наложено связей. Об учете связей речь пойдет далее.

На узел действует внешняя узловая нагрузка, характеризующаяся вектором 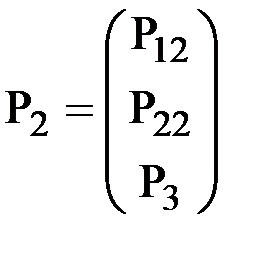, передаваемая на элементы, которые соединяются в этом узле. Пусть это будут три элемента под номерами 1, 2 и 3 (рис.28). Усилия, передаваемые на элемент е в узле 2, в соответствии с введенным ранее обозначением образуют вектор 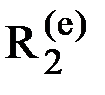Соответственно, со стороны элементов на узел передаются равные, но противоположно направленные усилия. Т.е. со стороны элемента е на узел действует система усилий, образующих вектор 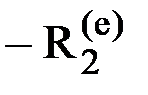. Узел элемента должен находиться в равновесии под действием внешних усилий и усилий, приложенных к узлу со стороны элементов. Следовательно можно записать:

.

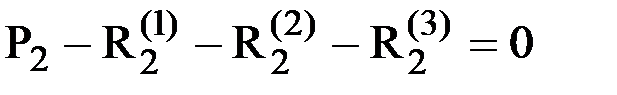(8)

Следует помнить, что данное равенство - матричное равенство и соответствует системе равенств, каждое из которых представляет собой уравнение равновесия усилий, действующих на узел по одному из направлений. Так как узел 2- жесткий, это равенство принимает следующий вид (рис.29):

.

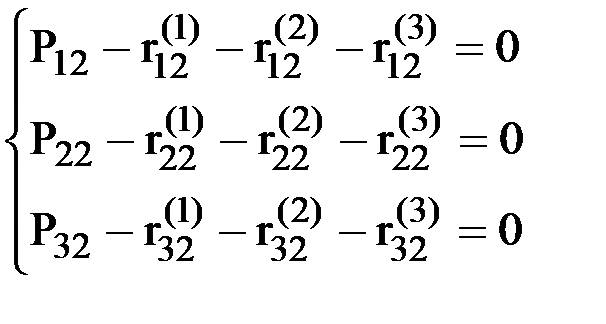В дальнейшем, для упрощения выкладок будем пользоваться матричной формой записи, не раскладывая равенства покомпонентно.

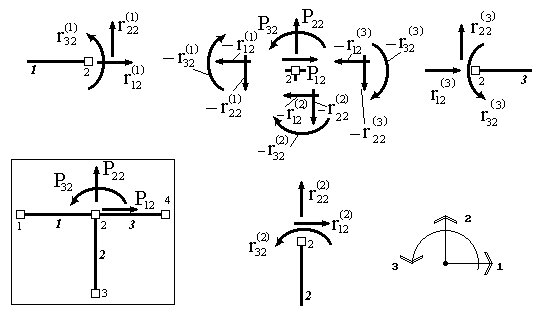Рис. 29

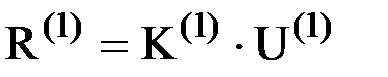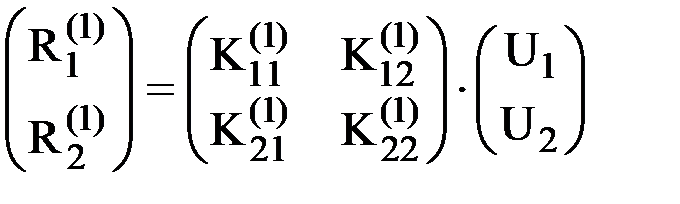В соответствии с (2) для элемента 1 справедливо соотношение или . Из него вектор усилий, действующих на узел 2 со стороны элемента 1, окажется равным .

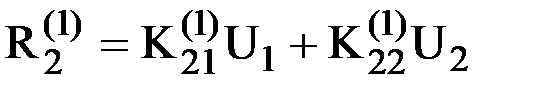Аналогично, для элемента 2 будем иметь: 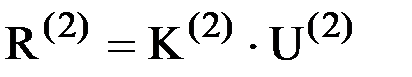или 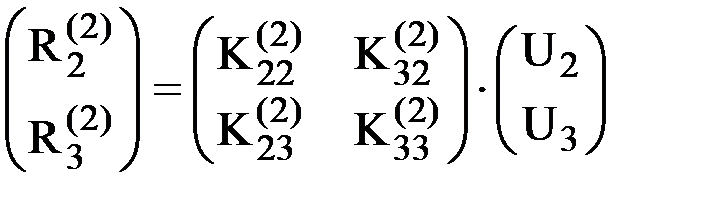. Из него вектор усилий, действующих на узел 2 со стороны элемента 2 окажется равным .

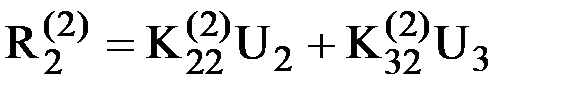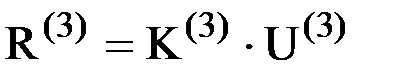Аналогично, для элемента 3 будем иметь: или 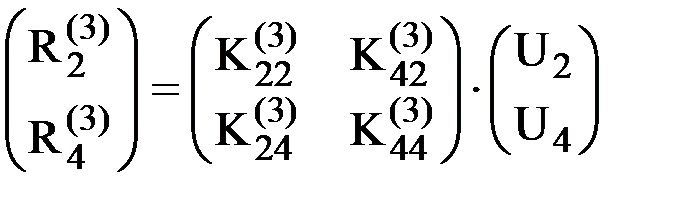. Из него вектор усилий, действующих на узел 2 со стороны элемента 3 окажется равным .

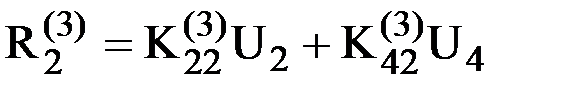Подставив полученные выражения в (8), получим:

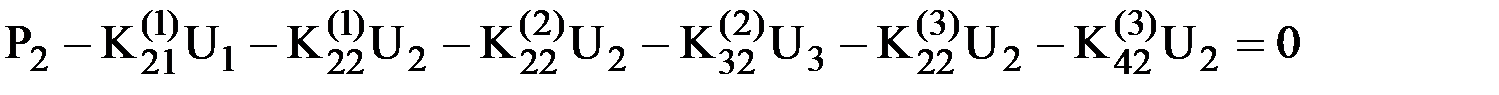, откуда:

.

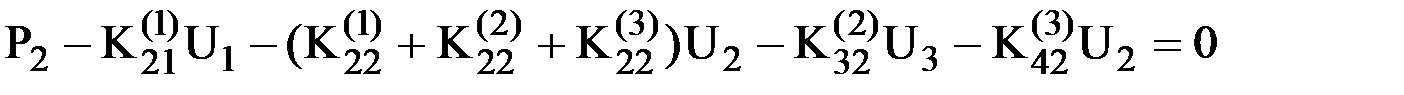Отсюда видно, что в уравнение равновесия для узла входят компоненты матриц жесткости только тех элементов, которые примыкают к этому узлу. Кроме того, в это уравнение входят перемещения только тех узлов, которые принадлежат элементам, примыкающим к рассматриваемому узлу.

Повторив аналогичные операции для всех узлов конечно-элементной схемы, изображенной на рис.28, получим:

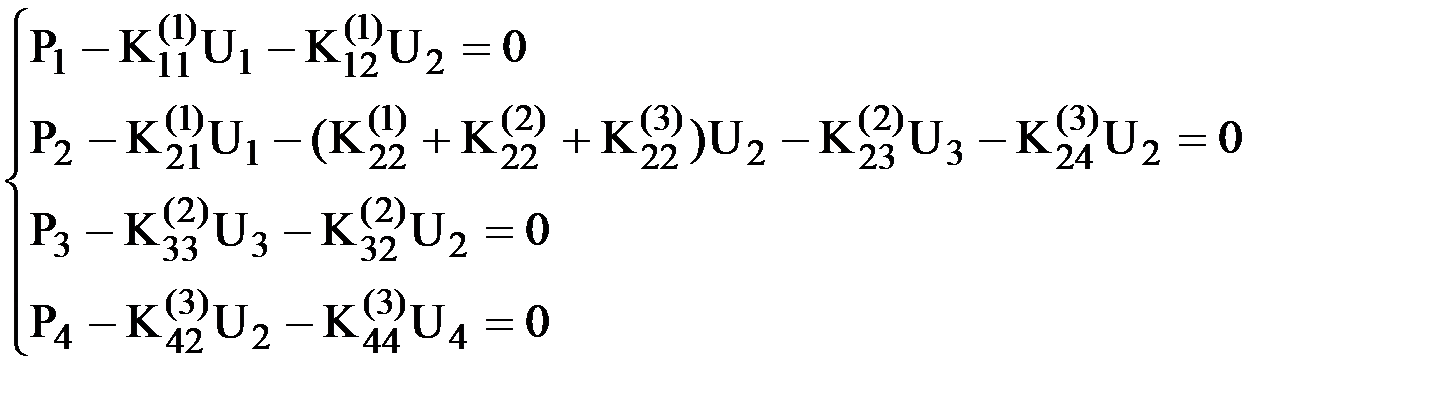
Запишем эту систему в матричной форме:

.

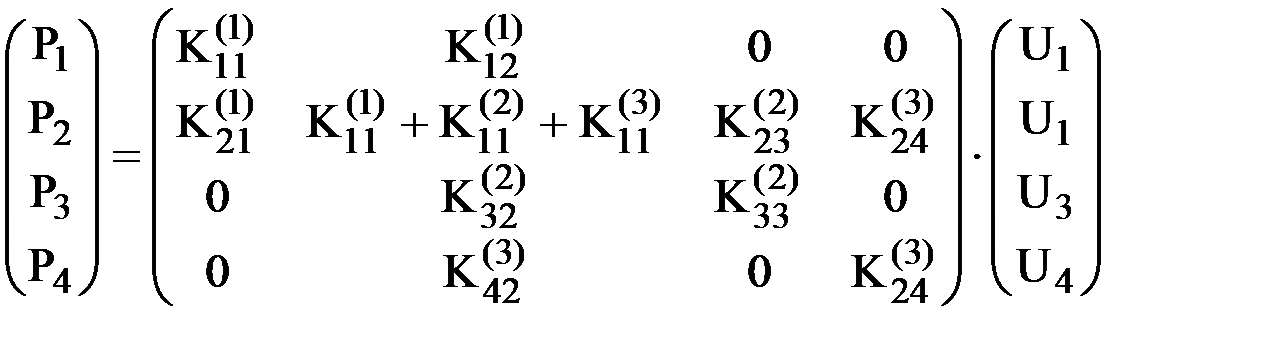(9)

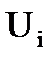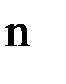Введем вектор перемещений узлов конечно-элементной сетки U, компонентами которого являются перемещения по направлению всех степеней свободы системы. Очевидно, этот вектор состоит из блоков - векторов перемещений всех узлов системы: .

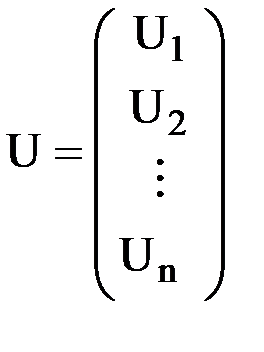Аналогично, введем вектор внешних узловых усилий P, действующих на конечно-элементную схему. Этот вектор также будет состоять из блоков - векторов усилий Р_i, действующих на каждый узел системы:

.

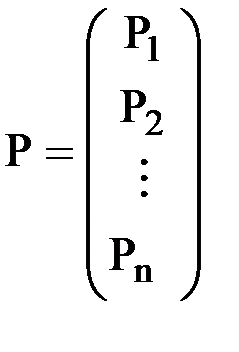Тогда полученная выше система уравнений (9) может быть записана в виде:

Зависимость (10) устанавливает связь между перемещениями узлов конечно-элементной сетки и приложенными к ним узловыми воздействиями. Зависимость (10) аналогична зависимости (2), но она построена не для отдельного элемента, а для всей конечно-элементной схемы. Матрица К, как и матрица жесткости элемента, связывает перемещения узлов и приложенные к ним воздействия, но не для одного элемента, а сразу для всей системы. Поэтому ее называют матрицей жесткости конечно-элементной схемы или глобальной матрицей жесткости.

Глобальная матрица жесткости - квадратная матрица, размером равным числу степеней свободы системы, имеющая, как видно из (9) блочную структуру.

Из (9) легко заключить, что блок 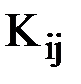глобальной матрицы жесткости формируется из блоков 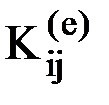матриц жесткости элементов е, входящих в конечно-элементную схему, причем представляет собой сумму блоков 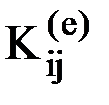для тех элементов конечно-элементной схемы, в состав которых входит узел i:

,

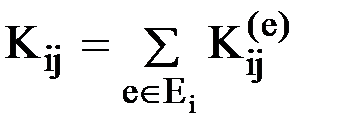(11)

где запись 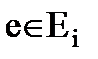и означает, что элемент е должен принадлежать множеству элементов, в состав которых входит узел i.

Действительно, в рассмотренном примере (рис.21) узел 2 входит в состав трех элементов 1, 2 и 3, значит блок 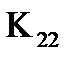формируется из соответствующих блоков матриц жесткости этих трех элементов путем их прямого суммирования. Но ни один элемент не соединяет, например, узлов 1 и 3, следовательно блок 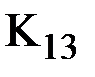глобальной матрицы жесткости представляет собой нулевую матрицу.

В системе (10) вектор внешних сил Р задается, глобальная матрица жесткости К, как мы только что выяснили, формируется из матриц жесткости элементов, входящих в конечно-элементную сетку. Неизвестными в этой системе являются перемещения узлов сетки, составляющие компоненты вектора U.

Таким образом, после построения вектора внешних нагрузок и формирования глобальной матрицы жесткости конечно-элементной схемы перемещения ее узлов определяются посредством решения системы линейных алгебраических уравнений МКЭ (10).

Легко показать, что в силу симметрии матриц жесткости элементов и в соответствии с (11) глобальная матрица жесткости также будет симметричной.

Рис. 30

Если на перемещения какого-либо из узлов конечно-элементной схемы наложены ограничения (рис.30), то уравнения равновесия для этого узла теряют смысл. Действительно, все приложенные к этому узлу силы, как внешняя нагрузка, так и усилия, действующие со стороны стержней, будут восприниматься опорными связями. Зато, заранее известны перемещения по направлениям закрепленных степеней свободы такого узла. Поэтому, в системе уравнений (10) для тех степеней свободы, на которые наложены ограничения, соответствующие уравнения равновесия заменяются уравнениями, в которых перемещениям присваиваются заданные значения.