Классификация математических моделей 2 страница
Как правило, построение математической модели - процесс итерационный. Например, на этапе составления математического описания приходится периодически возвращаться к предыдущим этапам для корректировки и дополнения их результатов. При этом могут вноситься изменения в состав входных параметров для упрощения математического описания и исключаться часть выходных параметров, если не обеспечивается необходимая точность их оценки с помощью располагаемых методов описания зависимостей между "входом" и "выходом" и т.п. Важным элементом этого процесса является разработка и использование имеющегося программного обеспечения. Средства программного обеспечения в системах автоматизированного проектирования представляют инженеру ряд возможностей при подготовке вычислительного эксперимента, а именно:
- возможность построения различных вычислительных схем из отдельных программных модулей;
- возможность декомпозиции модели для уменьшения требуемой оперативной памяти ЭВМ;
- возможность автономного программирования отдельных элементов-модулей математической модели и т.д.
Традиционно сложилась определенная схема выполнения экспериментов с математическими моделями (технология моделирования), которая в значительной мере повторяет технологию физического (натурного) эксперимента. В соответствии с этой технологией модель рассматривается как "черный ящик", имеющий входы 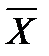 и выходы
и выходы 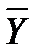 . В качестве первого шага производится выбор параметров X и Y, которые представляют интерес для исследователя или проектировщика на данном этапе его работы. Далее определяется план эксперимента, т.е. процедура выбора входных параметров Х1, Х2, Х2, ……. , на которые требуется знать отклик модели, т.е. значения Y1, Y1, ….. . Выбор плана зависит от конкретной цели исследования. В задачах оптимизации в качестве выхода рассматривается тот или иной критерий, а план эксперимента представляет собой выбор последовательности значений Х2, Х2, ……. в соответствии с принятым методом оптимизации.
. В качестве первого шага производится выбор параметров X и Y, которые представляют интерес для исследователя или проектировщика на данном этапе его работы. Далее определяется план эксперимента, т.е. процедура выбора входных параметров Х1, Х2, Х2, ……. , на которые требуется знать отклик модели, т.е. значения Y1, Y1, ….. . Выбор плана зависит от конкретной цели исследования. В задачах оптимизации в качестве выхода рассматривается тот или иной критерий, а план эксперимента представляет собой выбор последовательности значений Х2, Х2, ……. в соответствии с принятым методом оптимизации.
В результате экспериментов, помимо решения непосредственных задач исследований, определяется и эффективность используемой модели, что позволяет провести ее доработку. Так, при слабой зависимости выходных параметров от того или иного входного параметра (или параметров) появляется возможность исключить этот параметр из рассмотрения и тем самым упростить математическую модель. Таким образом, итерационные циклы характерны и для этой фазы моделирования. В последнее время данная технология моделирования видоизменяется в направлении учета структуры и динамики реализованных на ЭВМ моделей при организации экспериментов, т.е. модель является уже "прозрачным" ящиком. Это позволяет сделать процесс более эффективным как с точки зрения получения обоснованных оценок показателей так и с точки зрения затрат вычислительных ресурсов. Общая идея таких экспериментов заключается в использовании аналитических методов для определения перечня показателей, требующих оценки, и реализованных на ЭВМ вычислительных процедур - для нахождения значений этих показателей. Подобный подход является более целесообразным, нежели традиционный, в особенности при изучении класса систем, что имеет место, в частности, при проектировании.
ЛЕКЦИЯ № 7. Железнодорожный вагон как объект моделирования.
7.1. Виды моделируемых динамических процессов, возникающих при движении вагонов по рельсовой колее.
При эксплуатации подвижного состава на него действуют силы и под их воздействием перемещаются элементы и узлы вагона, изменяются усилия в несущих узлах вагона, появляются напряжения. Под динамическим процессом понимается временная зависимость действующих в узлах и элементах вагонов усилий, напряжений, ускорений и т.д.
Когда нужно регистрировать эти процессы ?
1. При испытаниях на прочность.
2. При испытаниях на ходовые качества вагона.
В вагоностроении различают:
1. Ходовые динамические испытания.
2. Ходовые прочностные испытания.
3. Испытания на соударения.
4. Стендовые испытания – на усталость.
Дадим определения этих видов испытаний:
1. Ходовые динамические испытания – это определение и оценка ходовых качеств вагона при различных скоростях движения и режимах нагружения на характерных участках ж.д. пути.
2. Ходовые прочностные испытания – это определение динамических напряжений в основных несущих элементах и узлах конструкций вагонов, а также динамических усилий при различных скоростях движения и режимах нагружения на характерных участках ж.д. пути. С целью уточнения прочности несущих конструкций и локализации зон концентрации напряжений.
3. Испытания на соударения – это исследование и оценка НДС, прочности и устойчивости вагона и его отдельных конструктивных узлов при ударе в автосцепку с заданными силой или скоростью соударения.
4. Стендовые испытания на усталость – это исследование сопротивления усталости несущей конструкции вагона в целом и его отдельных узлов при заданных режимах вибрационного или ударного нагружения.
При ходовых динамических испытаниях регистрируют:
- статический и динамический прогибы рессорного подвешивания.
- характер и частоты колебаний вагонов при его движении ( колебания кузова, рам тележек и т.д.).
- вертикальные и горизонтальные ускорения кузова вагона в зоне пятников (для пассажирских вагонов – в средней части кузова).
- динамические напряжения в надрессорных балках и раме тележки.
- динамические боковые (рамные) силы, действующие на буксы к.п.
При ходовых прочностных испытаниях регистрируют:
- динамические напряжения в исследуемых элементах и узлах конструкций вагонов.
- динамические усилия, действующие на исследуемые узлы и элементы вагона, а также их ускорения.
По результатам ходовых испытаний определяют:
- коэффициенты динамической перегрузки рессор.
- величины боковых (рамных) сил.
- вертикальный и горизонтальный коэффициент динамики.
- показатели плавности хода вагона.
- коэффициенты запаса устойчивости к.п. от схода вагона с рельсов.
Для пассажирских вагонов – основной динамический критерий – показатель плавности хода вагона.
Для грузовых вагонов –это вертикальный коэффициент динамики, величины боковых (рамных) сил, коэффициенты запаса устойчивости к.п. от схода вагона с рельсов.
7.2. Статистическая их обработка и оценка ходовых динамических и прочностных качеств вагонов.
Рассмотренные в 3.1. динамические показатели – случайные величины. Их предельные значения регламентированы “Нормами для расчета и проектирования…”. Для получения достоверных результатов используются методы математической статистики.
Процессы:
1. Периодические.
2. Непериодические.
3. Случайные.
Периодические процессы:
1. Гармонические.
2. Полигармонические.
Эти типы процессов чаще всего встречаются при стендовых испытаниях вагонов и т.д.
Рассказать о видах процессов, возникающих при испытаниях вагонов и методах их статистической обработки – минимум, максимум, среднее, стандарт, дисперсия, автокорреляционная функция, спектральная плотность мощности.
ЛЕКЦИЯ № 8. Метод конечных элементов.
8.1. Краткая история создания и использования МКЭ.
Возникновение метода конечных элементов (МКЭ) связано с решением задач космических исследований (1950 г.). Этот метод возник из строительной механики и теории упругости, а уже потом был осмыслен математиками, которые часто называют данный метод вариационно-разностным, подчеркивая тем самым его математическую природу. Они занимаются математическим обоснованием МКЭ, т.е. проводят теоретический анализ его сходимости и точности результатов. Представители же инженерного направления решают довольно сложные технические задачи, часто не задумываясь над строгим обоснованием применяемых ими приемов, а построенные алгоритмы и программы проверяют на известных точных решениях.
Существенный толчок в своем развитии МКЭ получил после того, как в 1963 г. было доказано, что этот метод можно рассматривать как один из вариантов известного в строительной механике метода Рэлея-Ритца, который путем минимизации потенциальной энергии позволяет свести задачу к системе линейных уравнений равновесия.
Связь МКЭ с процедурой минимизации позволила широко использовать его при решении задач в других областях техники. Метод применялся к задачам, описываемым уравнениями Лапласа или Пуассона (например, электромагнитные поля). Решение этих уравнений также связано с минимизацией некоторого функционала. Известны решения с помощью этого метода задач распространения тепла, задач гидромеханики и, в частности задач о течении жидкости в пористой среде.
Область применения МКЭ существенно расширилась, когда в 1968 г. было показано, что уравнения, определяющие элементы в задачах строительной механики, распространения тепла, гидромеханики, могут быть легко получены с помощью таких вариантов метода взвешенных невязок, как метод Галёркина или способ наименьших квадратов. Установление этого факта сыграло важную роль в теоретическом обосновании МКЭ, т.к. позволило применять его при решении многих типов дифференциальных уравнений. Таким образом, метод конечных элементов из численной процедуры решения задач строительной механики превратился в общий метод численного решения дифференциальных уравнений или систем дифференциальных уравнений. Этот прогресс был достигнут за довольно короткий срок, благодаря совершенствованию компьютерной техники.
Основные идеи МКЭ.
Основная идея метода конечных элементов (МКЭ) состоит в том, что любая непрерывная величина (температура, давление, перемещение) аппроксимируется дискретной моделью, построение которой выполняется на множестве кусочно-непрерывных функций, определенных на конечном числе подобластей. Алгоритм построения дискретной модели изучаемой непрерывной величины заключается в следующем:
• В рассматриваемой области фиксируют конечное число точек. Эти точки в
дальнейшем называют узлами.
• Полагают, что исследуемая непрерывная величина в каждом узле является переменной, подлежащей определению в процессе решения задачи.
• Область изменения непрерывной величины разбивают на элементы. Эти элементы имеют между собой общие узлы и, в совокупности, аппроксимируют форму области в целом.
• Непрерывную величину аппроксимируют в пределах каждого элемента
полиномом, коэффициенты которого рассчитывают на основании значений этой величины в узлах. Каждый элемент аппроксимируют своим
полиномом, а коэффициенты полиномов подбирают таким образом, чтобы сохранялась непрерывность величины вдоль границ соседних элементов.
Метод конечных элементов (МКЭ) - основной метод современной строительной механики, лежащий в основе подавляющего большинства современных программных комплексов, предназначенных для выполнения расчетов строительных конструкций на ЭВМ. МКЭ также используется для решения других разнообразных задач как в области прочностных расчетов, так и во многих других сферах, например задачах гидродинамики, электромагнетизма, теплопроводности и многих других.
Метод конечных элементов позволяет практически полностью автоматизировать расчет стержневых систем, хотя, как правило, требует выполнения значительно большего числа вычислительных операций по сравнению с классическими методами строительной механики. Однако, в современных условиях большой объем вычислений не является серьезной проблемой, и, в связи с этим, при внедрении ЭВМ в инженерную практику МКЭ получил широчайшее распространение[1]. Поэтому, знание основ метода конечных элементов и современных программных средств, позволяющих на его основе решать разнообразные задачи, в наше время для инженера является абсолютно необходимым.
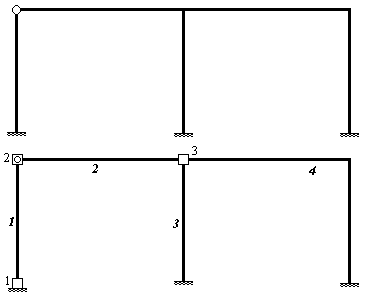 Рис. 1
Рис. 1
|
В МКЭ стержневая система мысленно разбивается на отдельные части - конечные элементы, соединяющиеся между собой в узлах (рис.1). Узлы могут быть жесткими и шарнирными. Совокупность соединенных между собой и прикрепленных к основанию конечных элементов образует расчетную схему метода, называемую конечно-элементной схемой или конечно-элементной модельюили просто системой элементов. Элементы и узлы конечно-элементной схемы нумеруются.
Внешняя нагрузка считается приложенной только в узлах конечно-элементной схемы. В общем случае переход от заданной нагрузки к узловой осуществляется следующим образом. На основании принципа суперпозиций рассматриваемое состояние стержневой системы может быть представлено как сумма двух состояний (рис.2). В первом состоянии (задача1) вводятся связи, препятствующие всем возможным смещениям узлов системы, аналогично тому, как образуется основная система в методе перемещений. При этом, однако, продольными деформациями стержней не пренебрегают. От действия заданных нагрузок во введенных связях возникают реакции. Во втором состоянии (задача 2) узлы конечно-элементной схемы не закреплены от смещений, но к ним прикладываются усилия равные по модулю реакциям в связях, определенным в первом состоянии, но противоположные им по направлению (рис.2). Расчет системы в первом состоянии не представляет труда. В частности, если конечно-элементная схема создается таким образом, чтобы элементы представляли собой отдельные стержни (элементы 1, 2 и 3 на рис.2), то для каждого из таких элементов имеется табличное решение (таблица 11.1), позволяющее определить реакции в связях и построить эпюры внутренних усилий по их длине. Для расчета же системы во втором состоянии, т.е. для решения задачи 2, и применяется метод конечных элементов. Окончательное решение задачи будет представлять собой сумму решений этих двух задач.
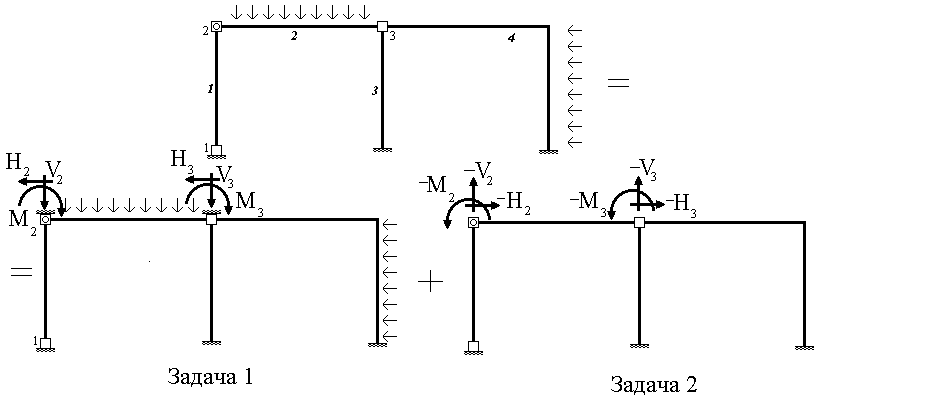 Рис. 2 Рис. 2
|
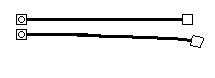 Рис. 3
Рис. 3
|
В задаче 2 усилия, действующие на любой элемент приложены исключительно в узлах. В этом случае перемещения узлов любого элемента, взятого в отдельности (рис.3), однозначно определяют усилия и перемещения в любой точке этого элемента. Как известно, для стержневых систем решение такой задачи может быть найдено точно.
Каждый, взятый отдельно от системы, конечный элемент должен быть достаточно простым, чтобы имелась возможность легко определить перемещения и усилия в любом сечении стержней элемента по заданным перемещениям его узлов. Связь между перемещениями узлов элемента и усилиями в них задается при помощи матрицы жесткости элемента. Количество перемещений узлов элемента, которые однозначно определяют состояние данного элемента называют числом степеней свободы элемента. Оно определяется по формуле:
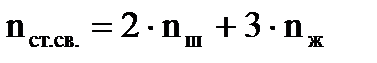 , ,
| (1) |
где 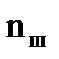 -число шарнирных узлов в элементе, а
-число шарнирных узлов в элементе, а 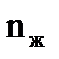 - число жестких узлов в элементе. Действительно, если узел представляет собой шарнир, то его положение на плоскости можно охарактеризовать двумя линейными перемещениями, например в вертикальном и горизонтальном направлениях. В случае жесткого узла необходимо еще дополнительно к линейным смещениям задать его поворот.
- число жестких узлов в элементе. Действительно, если узел представляет собой шарнир, то его положение на плоскости можно охарактеризовать двумя линейными перемещениями, например в вертикальном и горизонтальном направлениях. В случае жесткого узла необходимо еще дополнительно к линейным смещениям задать его поворот.
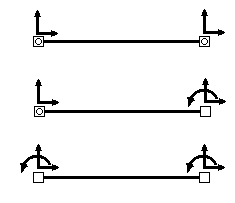 Рис. 4
Рис. 4
|
На рис.4 первый элемент имеет характеризуется четырьмя степенями свободы, т.к. он содержит два шарнирных узла. При отсутствии нагрузки, кроме приложенной в самих узлах, положение на плоскости любой точки этого элемента определяется четырьмя параметрами - двумя вертикальными и двумя горизонтальными перемещениями узлов элемента. У второго элемента на рис.4 - пять степеней свободы - к четырем линейным смещениям добавляется поворот в одном из узлов. У третьего элемента - шесть степеней свободы, которым соответствуют четыре линейных и два угловых перемещения.
Аналогично, для всей конечно-элементной схемы вводятся матрица жесткости системыилиглобальная матрица жесткости, устанавливающая связь между перемещениями узлов системы и усилиями в них, а также число степеней свободы системы или глобальное число степеней свободы- количество перемещений узлов системы, которые достаточно знать, чтобы однозначно определить состояние всей системы. Оно также определяется по формуле (1), в которой 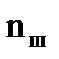 -число шарнирных узлов, а
-число шарнирных узлов, а 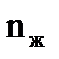 - число жестких узлов во всей конечно-элементной схеме.
- число жестких узлов во всей конечно-элементной схеме.
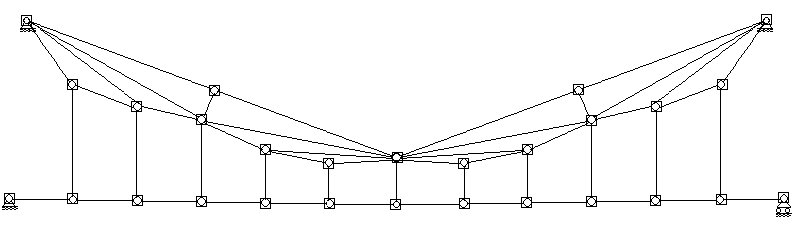 Рис. 5
Рис. 5
|
Например, при расчете методом конечных элементов висячей системы, приведенной на рис.х.10, может использоваться конечно-элементная схема, изображенная на рис.5. Она содержит в себе 28 шарнирных узлов, следовательно характеризуется 56 степенями свободы.
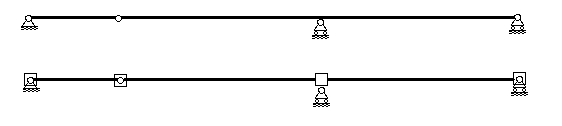 Рис. 6
Рис. 6
|
В конечно-элементной схеме балки (рис.6) используется один жесткий и три шарнирных узла. Следовательно, в соответствии с (1) эта схема характеризуется 3×2+1×3=9 степенями свободы.
Для всех элементов, из которых состоит конечно-элементная схема, должны быть построены матрицы жесткости элементов. В программных комплексах, реализующих алгоритм метода конечных элементов, хранятся готовые матрицы жесткости для элементов различных типов.
На практике, при расчете плоских стержневых систем используют готовые матрицы жесткости для элементов только трех типов: простых стержней с двумя жесткими узлами, двумя шарнирными узлами, одним жестким и одним шарнирным узлом (рис.4). В этом случае при разбивке стержневой системы на элементы узлы вводятся в местах соединения и изломов стержней, в опорах, шарнирах и на свободных концах консольных стержней. В принципе узел может быть введен и в любых других точках, например, в точках приложения сосредоточенных сил..
В учебных целях могут использоваться и элементы других типов (рис.7), в том числе и включающие в себя опорные закрепления.
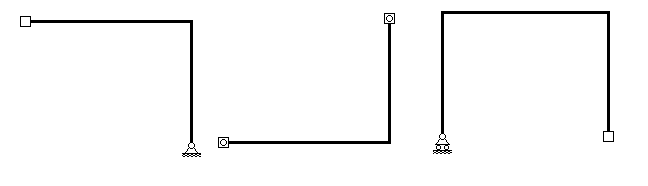 Рис. 7
Рис. 7
|
Из построенных матриц жесткости элементов формируется матрица жесткости системы. Для этого все матрицы жесткости элементов и матрица жесткости системы должны быть сформированы в единой системе осей координат, называемой глобальной системой осей координат. При расчете плоских стержневых систем традиционно используется следующая глобальная система осей координат (рис.8): ось1 направлена вправо, ось 2 - вверх, ось 3 - против часовой стрелки.
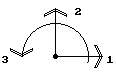 Рис. 8
Рис. 8
|
Матрицы жесткости элементов могут формироваться и храниться в памяти ЭВМ в своих, локальных системах осей координат, в общем случае отличных от глобальной системы осей координат. В данной ситуации при помощи специальной процедуры эти матрицы должны быть перестроены для глобальной системы осей координат.
Так как матрица жесткости системы устанавливает связь между усилиями, приложенными к ее узлам и перемещениями ее узлов, то имея построенную матрицу жесткости системы и зная внешнюю узловую нагрузку, можно найти перемещения всех узлов конечно-элементной схемы. Для этого требуется решить систему линейных алгебраических уравнений. Порядок этой системы равен числу ее степеней свободы.
По известным перемещениям узлов системы для каждого элемента при помощи имеющихся матриц жесткости элементов можно найти внутренние усилия в элементах от действия нагрузки, приложенной в узлах (задача 2). Окончательное решение задачи, как уже упоминалось, ищется как сумма решений задачи 1 и задачи 2.
Таким образом, метод конечных элементов в данном виде аналогичен методу перемещений, так как сначала определяются перемещения узлов системы, а затем по ним - деформации и усилия в стержнях. Возможна реализация метода конечных элементов и в форме метода сил, однако она имеет ряд существенных недостатков и поэтому представляет большей частью чисто научный, но не практический интерес.
Итак, расчет стержневой системы методом конечных элементов в форме метода перемещений состоит из следующих этапов:
Создание конечно-элементной схемы (разбивка системы на элементы и их нумерация).
Сведение заданной внешней нагрузки к узловой.
Формирование матриц жесткости всех элементов системы в локальных системах координат и их преобразование в глобальную систему координат.
Формирование глобальной матрицы жесткости, системы уравнений метода конечных элементов и ее решение.
Определение усилий в элементах от действия узловой нагрузки.
Определение окончательных значений усилий в элементах путем сложения решений задач 1 и 2.
Далее подробно рассмотрим все эти этапы.
Конечный элемент. Матрица жесткости конечного элемента.
Рассмотрим произвольный конечный элемент с числом степеней свободы nст.
Вектором узловых перемещений конечного элемента называется вектор, складывающийся из значений перемещений его узлов по направлению всех его степеней свободы. Очевидно, размерность вектора узловых перемещений равна числу степеней свободы элемента nст.
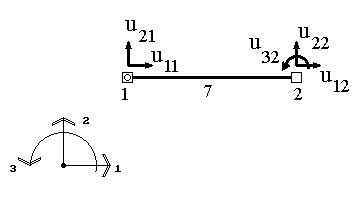 Рис. 9
Рис. 9
|
Например, для двухузлового элемента, имеющего в конечно-элементной схеме номер 7, характеризующегося тремя степенями свободы (рис.9), вектор узловых перемещений будет иметь следующий вид: 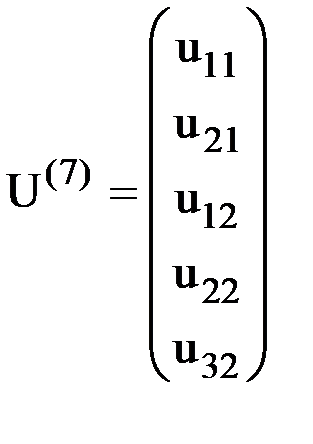 .
.
Здесь введены следующие обозначения: 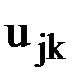 - перемещение узла k по направлению j,
- перемещение узла k по направлению j, 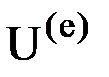 -вектор узловых перемещений узла е. Понятно, что если узел k шарнирный, то j может быть равно 1 или 2. Если же узел k жесткий, то j может быть равно 1, 2 или 3.
-вектор узловых перемещений узла е. Понятно, что если узел k шарнирный, то j может быть равно 1 или 2. Если же узел k жесткий, то j может быть равно 1, 2 или 3.
Аналогично вводится вектор узловых усилий, действующих на элемент. Его компонентами являются усилия, приложенные к элементу в узлах и действующие по направлению всех его степеней свободы. Для приведенного на рис.9 элемента этот вектор будет иметь вид (рис.10):
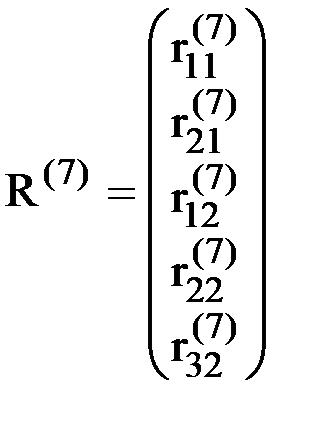 .
.
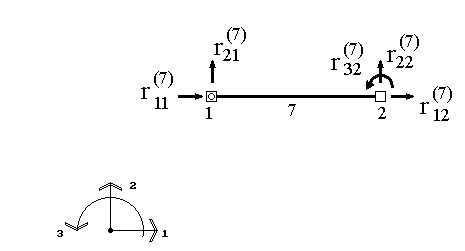 Рис. 10
Рис. 10
|
Здесь вводятся обозначения: 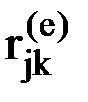 - усилие, действующее на узел k элемента е по направлению j,
- усилие, действующее на узел k элемента е по направлению j, 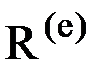 - вектор узловых сил, дейсвующих на элемент е.
- вектор узловых сил, дейсвующих на элемент е.
Вектора R(e) и U(e) являются блочными, т.е. в них можно выделить блоки 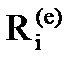 и
и 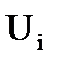 соответственно, содержащие усилия и перемещения, относящиеся к i-ому узлу элемента. Если узел i - жесткий, то
соответственно, содержащие усилия и перемещения, относящиеся к i-ому узлу элемента. Если узел i - жесткий, то 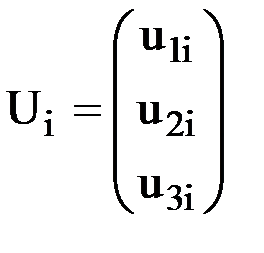 , если шарнирный, то
, если шарнирный, то 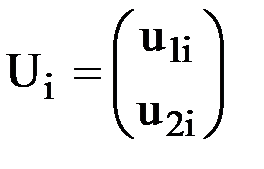 . Аналогично выглядят и блоки вектора R(e).
. Аналогично выглядят и блоки вектора R(e).
Например, для рассматриваемого элемента (рис.9 и рис.10):
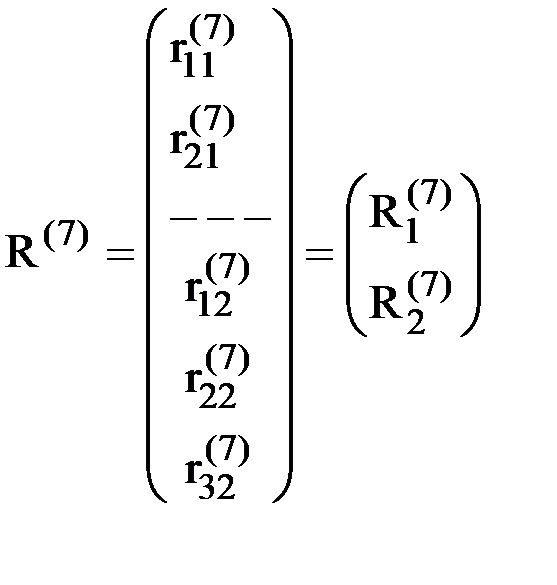 ,
, 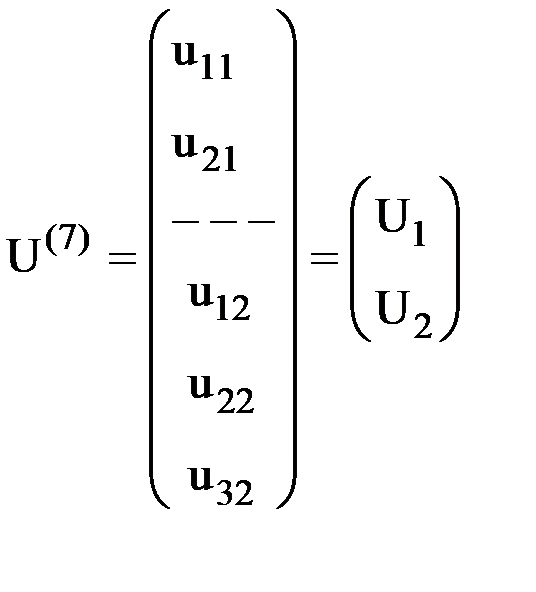 .
.
Понятно, что при деформировании элемента в результате смещения одного из его узлов по направлению одной из степеней свободы на узлы элемента должны действовать внешние силы, препятствующие возвращению элемента в недеформируемое состояние. Подобная ситуация может возникнуть, например, при неравномерных осадках в опорах статически неопределимой стержневой системы (рис.12),- реакции, возникшие в опорах, препятствуют возвращению конструкции в недеформированное состояние. В рамках гипотезы линейного деформирования связь между перемещениями узлов элемента и силами, действующими при этом на него, должна быть линейной. Например, с увеличением смещения d вдвое, все усилия, действующие на узлы элемента также должны увеличиться вдвое.
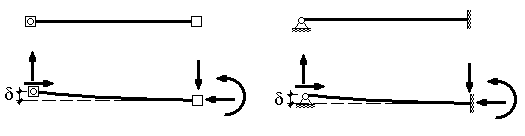 Рис. 11
Рис. 11
|
Основной характеристикой конечного элемента является матрица жесткости элемента 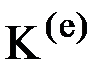 . Она связывает вектор узловых перемещений
. Она связывает вектор узловых перемещений 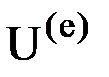 и вектор приложенных к элементу узловых усилий
и вектор приложенных к элементу узловых усилий 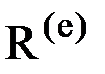 соотношением:
соотношением:
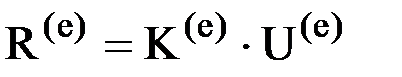 , ,
| (2) |
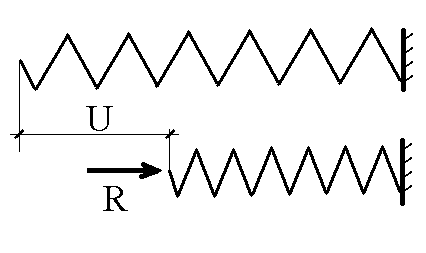 Рис. 12
Рис. 12
|
выражающим линейный характер связи между действующими на узлы силаи и узловыми перемещениями. Матрица жесткости элемента играет роль, аналогичную коэффициенту жесткости пружины К, связывающего приложенное к ней усилие R, и вызванное этим усилием перемещение U соотношением (рис.12) 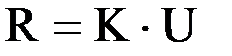 .
.
Поскольку вектора 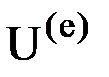 и
и 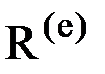 имеют размерность
имеют размерность 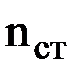 , число строк и столбцов в матрице
, число строк и столбцов в матрице 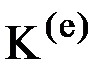 тоже должно быть равным
тоже должно быть равным 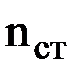 :
:
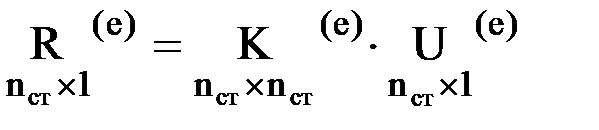 .
.
Введем обозначение 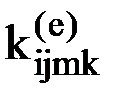 - усилие, действующее на узел m элемента e по направлению i, от единичного перемещения узла k этого же элемента е по направлению j при условии, что перемещения по направлению всех остальных степеней свободы в элементе равны нулю. Например,
- усилие, действующее на узел m элемента e по направлению i, от единичного перемещения узла k этого же элемента е по направлению j при условии, что перемещения по направлению всех остальных степеней свободы в элементе равны нулю. Например, 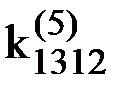 - усилие, действующее на узел 1 элемента 5 по направлению 1 при единичном перемещении узла 2 этого же элемента 5 по направлению 3, а
- усилие, действующее на узел 1 элемента 5 по направлению 1 при единичном перемещении узла 2 этого же элемента 5 по направлению 3, а 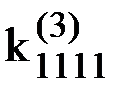 - усилие, действующее на узел 1 элемента 3 по направлению 1 от единичного смещения этого же узла по этому же направлению. Последнее значение, как и любое значение
- усилие, действующее на узел 1 элемента 3 по направлению 1 от единичного смещения этого же узла по этому же направлению. Последнее значение, как и любое значение 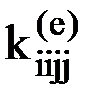 в соответствии с теоремой Клапейрона всегда положительно, аналогично коэффициентам
в соответствии с теоремой Клапейрона всегда положительно, аналогично коэффициентам 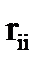 в уравнениях классического метода перемещений.
в уравнениях классического метода перемещений.
Важно четко помнить порядок индексов, стоящих при k. Верхний индекс - это номер элемента. Первые два нижних индекса - направления, причем первый из них - номер направления определяемого усилия, а второй - номер направления, в котором произошло единичное перемещение. Вторые два нижних индекса - номера узлов элемента, причем первый из них - номер узла, в котором определяется усилие, второй - в котором задано единичное перемещение.
Для рассматриваемого элемента (рис.9 и рис.10) матрица жесткости элемента имеет следующий вид:
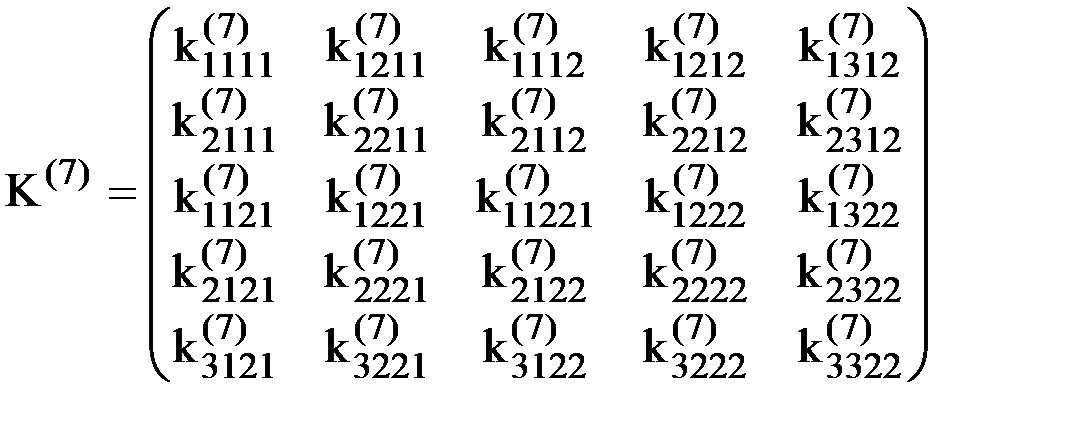 .
.
Дата добавления: 2015-12-16; просмотров: 1314;
