Математические модели

Дадим сначала определение терминов "математическая модель" и "математическое моделирование".

Математическая модель - это совокуп­ность математических объектов (чисел, переменных, векторов, мно­жеств и т.п.) и отношений между ними, которая адекватно отобра­жает некоторые свойства проектируемого технического объекта. В процессе проектирования применяют те математические модели, ко­торые отображают существенные с позиций инженера-проектировщика свойства объекта.

Под математическим моделированием понимают способ исследо­вания различных процессов путем изучения явлений, имеющих различ­ное физическое содержание, но описываемых одинаковыми математическими соотношениями.

Часто термин «математическое моделирование» относят не только к оперированию математической моделью, но и к ее построению. При построении и оперировании математическими моделями необходимо принимать во внимание ряд существенных обстоятельств. Свойства и режимы работы объекта проектирования (он же - объект моделирования) характеризуются совокупностью параметров, объединяемых в три группы:

выходные параметры («выходы») - показатели качества, по ко­торым можно судить о правильности функционирования системы и ко­торые зависят как от свойств элементов, так и от особенностей связи элементов друг с другом, т.е. структуры системы:

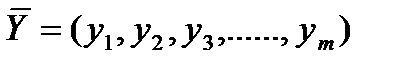- вектор выходных параметров;

внутренние параметры - это параметры элементов системы:

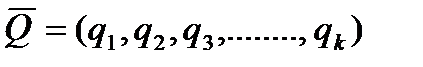- вектор внутренних параметров;

внешние параметры («входы») - это параметры внешней по отношению к объекту среды, оказывающие влияние на его функционирование:

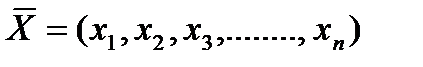- вектор внешних параметров.

Однако далеко не во всех случаях зависимость «выхода» от внутренних параметров и «входа» можно получить в явном виде, т.е., в форме аналитических моделей типа .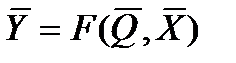

Более час­то в математической модели фигурируют так называемые фазовые переменные, с помощью которых описывается состояние объекта моде­лирования и которые не относятся к выходным, внутренним или внеш­ним параметрам. Из всего множества фазовых переменных при построении математической модели обычно используют те из них, совокупность которых обеспечивает однозначное определение состояния объекта. (Эти переменные часто называются "базисными координатами и обозначаются каким-либо вектором, например 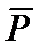). В таком случае математическая модель представляется в виде. 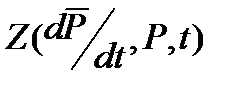= 0, где 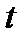– время. Внутренние параметры объекта фигурируют в этой модели в ка­честве коэффициентов при переменных.

Выходные параметры либо могут иметь смысл функционалов зависимостей фазовых переменных от времени, либо относится к пороговым. (Под функционалом понимается такой закон, в соответствии с ко­торым каждой функции из определенного класса функций соответствует значение некоторого числового параметра, т.е. функцио­нал есть отображение класса функций в класс чисел. Например, каждой одномерной функции, образующей тело вращения вокруг оси абсцисс, соответствует числовое значение объема этого тела).

В первом случае решению 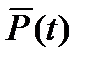соответствует несколь­ко значений функционалов - анализируемых выходных параметров. (Например, при решении задач внешней баллистики базисные координаты – это координаты снаряда и цели. Выходные координаты – точка встречи, время встречи). Во втором - в результате моделирования определяются те значения внешних воздействий на объект в процессе его функционирования, при которых его работоспособность или качество функционирования находятся в допустимых пределах. Например, к таким параметрам относится максимальная скорость движения вагона.

Принимая во внимание сказанное выше, рассмотрим теперь, ка­кими особенностями должно отличаться математическое описание си­стемы или процесса, выступая в качестве инженерной математиче­ской модели. Эти особенности мы назовем общесистемны­ми характеристиками.

Чтобы построить модель, необходимо искусственно вычленить из реального объекта (из системы или процесса) те элементы, кото­рые считаются при этом существенными. Каждому элементу ставится в соответствие переменная модели.

В общем случае операция вычленения существенных элементов реального объекта при построении модели является далеко не три­виальной, причем по самой логике моделирования эта операция дол­жна предшествовать выбору переменных и математических соотноше­ний для этих переменных. (К примеру, далеко не во всех случа­ях можно рассматривать ЛА как материальную точку). Вычленение су­щественных элементов определяется той содержательной инженерной задачей, для решения которой строится модель.

После того, как выделены элементы и выбраны соответствующие переменные, при построении модели и работе с ней вплоть до завершающего этапа - интерпретации результатов - исследователь опери­рует только с переменными, как бы забывая о реальном объекте: он работает с концептуальным объектом (т.е. с моделью реального объекта).

Классификация переменных и взаимосвязи параметров модели

В зависимости от стоящей перед исследователем задачи какие-то из переменных являются исходными параметрами, какие-то из них требуется определить в результате моделирования. Кроме того, в ряде задач значения некоторых переменных могут быть не заданы непосредственно условиями поставленной задачи и, в то же время, не являться искомыми (по смыслу поставленной задачи), характеристиками: это либо возмущения (неопределенные факторы типа слу­чайных отклонении от заданных параметров, неопределенных пара­метров внешней среды, активного внешнего противодействия), либо параметры управления.

Таким образом, переменные модели содержательно интерпретируются как:

• исходные параметры;
• параметры, характеризующие состояния объекта и/или его "выходы";
• возмущения;
• управления.

Если объектом моделирования является процесс или система с меняющимися во времени параметрами, то в рамках модели должны быть заданы начальные (исходные) состояния, либо определены про­цедуры ввода в модель начальных состояний в процессе работы с моделью (т.е. при моделировании). Множество допустимых начальных состояний, является существенной характеристикой модели. Состояния (в том числе и начальные состояния) должны быть соотнесены с переменными модели. В простейшем случае начальное состояние может определяться просто как совокупность значений исходных характеристик. С учетом этого положения, расширяя дан­ное выше определение, под математической моделью реального объек­та будем понимать совокупность соотношений (например, формул, уравнений, неравенств, логических условий, операторов и т.д.), определяющих характеристики состояния объекта (а через них и вы­ходные параметры) в зависимости от внутренних параметров, внешних воздействий (возмущений и управлений), начальных условий и време­ни .

Переменные модели связаны между собой соотношениями, которые задается в виде уравнений, неравенств и т.д. Система этих соотно­шений должна обладать необходимой полнотой и непротиворечивостью (совместностью) в том смысле, что при известных исходных парамет­рах с помощью математической модели могут быть однозначно опреде­лены выходные параметры. При этом, естественно, должно выполнять­ся условие детерминированности, означающее неслучайный характер этих соотношений. Если же начальные условия и внешние воздействия также не случайны, то модель оказывается вполне детерминированной

На практике, часто приходится рассматривать случайные процес­сы функционирования различных систем. Характеристики состояний системы для таких процессов оказываются случайными функциями вре­мени в силу различных причин, например, случайности возмущений или начальных условий либо их совокупности. В подобной ситуации при помощи математической модели одно­значно определяются распределения вероятностей параметров состо­яния системы, если заданы распределения вероятностей случайных переменных.

Уровень агрегирования

При системном рассмотрении объект моделирования представля­ет собой совокупность элементов, находящихся во взаимодействии между собой и с внешней средой, причем в рамках структуры объек­та как системы выделяются различные иерархические уровни.

Иерархическое представление объектов проектирования обуслов­ливает и их математическое представление, т.е. на каждом иерархическом уровне используются свои математические модели, сложность которых определяется задачами и возможностями анализа.

Уровень агрегирования модели объекта определяется тем, с элементами какого уровня иерархии объекта непосредственно соотносятся переменные модели.