Классификация математических моделей 1 страница

В зависимости от уровня агрегирования математические модели подразделяются на модели систем и модели элементов, а в зависимо­сти от способа образования моделей систем - на полные модели, получаемые непосредственным объединением моделей элементов и макромодели, являющиеся аппроксимацией полной модели.

В зависимости от моделируемых свойств объекта различают функциональные модели, в которых отображаются процессы функционирования, и структурные, выражающие состав и связи между элемента­ми объекта. Структурные модели могут быть реализованы в виде мат­риц и графов. Анализируя способы получения функциональных моделей, можно выделить группы теоретических и формальных моделей. В основе теоретических лежат изученные физические закономерности, эти модели более универсальны и применимы в широких диапазонах изменения ус­ловий функционирования объекта. Формальные модели формируются при рассмотрении объекта как "черного ящика".

По признакам, связанным с особенностями уравнений математиче­ских моделей они подразделяются на линейные и нелинейные, а также непре­рывные, в которых переменные непрерывны, и дискретные, переменные которых являются дискретными величинами. Кроме того, различия в форме связей между параметрами позволяют выделить модели в виде систем уравнений. Это будут алгоритмические модели. В виде же явных за­висимостей выходных параметров от внутренних и внешних представляются аналити­ческие модели.

Факт учета инерционности моделируемых процессов делает воз­можным разделить модели на динамические и статические.

В основе приведенной классификации лежит деление моделей на группы по признакам, практически не за­висящим от области применения модели и ее целевого назначения.

Ниже можно дать классификацию математических моделей с точки зрения их целевого назначения в САПР.

Математические модели для оценки проектных параметров.

Осно­ву моделей этого типа составляют алгоритмы расчета технических характеристик вагонов, его подсистем, узлов и элементов. Эти алгоритмы, в свою очередь, основаны на теоретических методах, которые излагаются в курсах динамики вагонов, прочности и других специальных инженерных дисциплинах. Заметим, что внедрение ЭВМ в процесс проектиро­вания начиналось именно с автоматизации проектных расчетов и яви­лось одной из предпосылок появления САПР.

Математические модели геометрии конструкции.

Модели этой группы основаны на объединении пакетов прикладных программ ввода, обработки и вывода графической информации с алгоритмами синтеза геометрии элементов конструкции и конструктивно-компоновочных схем, использующими в качестве входов оценки, проектных парамет­ров и пространственно-кинематические требования к характеристи­кам конструкции. Появление развитого терминального оборудования ЭВМ и реализация моделей этого типа позволили перейти от автома­тизации проектных расчетов непосредственно к реализации САПР.

Математические модели функционирования.

Потребность в моде­лях этого типа, о которых уже говорилось в предыдущем параграфе, появляется при переходе в рамках САПР от решения конструкторских задач и частных задач проектирования подсистем и узлов вагонов к системной оптимизации комплекса вагона в целом (к так называемой за­даче "оптимизации облика"). Место моделей функционирования в си­стеме моделей, используемых в САПР, определяется необходимостью автоматизации процедур перехода от проектно-конструктивных харак­теристик вагона к критериям оценки качества - вагону в целом.

Реализованные в виде программ алгоритмы моделей пере­численных трех типов являются основными в составе программного обеспечения САПР. Наряду с этими моделями необходимыми составля­ющими системы является ряд обеспечивающих моделей, перечисленных ниже. Речь идет не о сервисных программах, обеспечивающих ком­фортные условия взаимодействия проектировщика и конструктора с ЭВМ, а о моделях, обеспечивающих взаимную увязку и концептуаль­ную завершенность системы моделей и всего программного обеспече­ния САПР.

Модели этой группы в настоящее время еще не реализованы в САПР в полном виде, так же как не завершена и разработка подхо­дов к построению такого рода моделей.

Математические модели оптимизации.

Наряду с использованием хорошо разработанных за последние два десятилетия методов оптими­зации и процедур решения задач математического программирования, САПР предъявляет ряд специальных требований к моделям оптимизации, а именно:

- необходимость решения оптимизационных задач большой размер­ности при затратах машинного времени не более нескольких минут (для обеспечения непрерывного диалогового режима проектирования);

- алгоритмизация методов оптимизации иерархических систем (в связи с иерархической структурой системы основных математиче­ских моделей САПР);

- многокритериальная оптимизация проектных решений в авто­матизированном диалоговом режиме.

Математические модели технического риска.

Проблема техниче­ского риска возникает в связи с тем, что при создании сложных объектов перспективной техники, к которым относятся вагоны, использу­ется большое количество принципиально новых технических решений, причем разработка различных подсистем и их элементов ведется па­раллельно, что делает чрезвычайно сложной проблему взаимной увяз­ки подсистем из-за высокой степени неопределенности достижимых в результате разработки технических параметров. Самый простой, ка­залось бы, путь разрешения этой проблемы - за счет предусматри­ваемых заранее резервов практически не приемлем, так как при этом эффективность вагонов с применением новых решений может быть даже ниже, чем для вагонов того же типа, но созданного на базе отработанных схем. Назначение моделей технического риска - оценка уровней риска для различных уровней полноты реализации ожидаемых технических характеристик вагона в зависимости от неопределенности ожидаемых ха­рактеристик элементов подсистем. Методы оценки риска в настоящее время интенсивно разрабатываются.

Математические модели критериев.

Можно выделить два типа мо­делей критериев, соответствующих следующим возможным вариантам пред­ставления целей, ради достижения которых создается анализируемая система:

- критерии оценки эффекта могут быть выражены непосредствен­но через характеристики функционирования технической сис­темы;

- общие представления о конечных целях можно представить лишь через вторичные эффекты - характеристики внешней (по отношению к анализируемой) системы, или внешней среды.

Если во втором случае сфера применения анализируемой систе­мы может быть адекватно представлена соответствующей математиче­ской моделью, то формально проблема сводится к первому случаю пу­тём дополнения системы моделей моделью сферы применения. Входом такой модели являются обобщенные характеристики функционирования анализируемой технической системы, выходом - обобщенные характе­ристики сферы применения, через которые можно выразить критерии эффективности. Если адекватная формализация сферы применения не­возможна, модель критериев должна представлять собой систему со­держательно обоснованных или полученных экспертно процедур све­дения критериев к обобщенным характеристикам функционирования анализируемой технической системы. Модели критериев во многих случаях могут выступать лишь в виде концептуальной базы для определения принципов оптимальности проектируемой системы и не быть реализованной в виде алгоритмов, входящих в состав программного обеспечения САПР. До последнего времени разработка общих принципов построения моделей критериев остается не завершенной.

6.2 Требования, предъявляемые к математическим моделям

Как уже отмечалось процесс моделирования состоит из двух фаз. Первая фаза заключается в построении самой математической модели. На второй фазе проводится оперирование построенной моделью (при использова­нии ЭВМ можно говорить о проведении "вычислительного эксперимен­та") для получения необходимых данных об исследуемом объекте в форме конкретных числовых значений выходных параметров объекта и их зависимостей от входных внешних воздействий и внутренних па­раметров.

Рассмотрим ряд особенностей этих двух фаз.

Требования, предъявляемые к математическим моделям

Формулирование совокупности требований к математической мо­дели является важным элементом в процессе ее построения. Часть из этих требований носит универсальный харак­тер, т.е. справедлива по отношению к любой математической модели, а часть обусловлена использованием ЭВМ в качестве инструмента мо­делирования.

Основными требованиями к математической модели являют­ся требования точности, универсальности, экономичности.

Точность математической модели определяется степенью откло­нения полученных с ее помощью значений параметров моделируемого объекта от истинных значений этих параметров. Таким образом, если в качестве оценки параметра объекта y_i выбирается величи­на y*_i , полученная в результате моделирования, то для оценки точности будем использовать величину 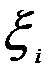= (y_i - y*_i). При определении точности модели необходимо учитывать ряд обстоятельств. Первое обстоятельство связано с тем, что точность модели в большинстве случаев моделирования сложных объектов приходится определять в условиях, когда эти объекты характеризуются несколькими парамет­рами. Следовательно, возникает задача оценки точности по несколь­ким критериям (т.е. векторной оценки).

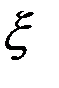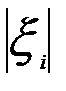В качестве критерия точности при многокритериальной оценке математической модели может быть использована либо т - норма вектора, т.е. = max , либо 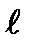- норма, т.е. 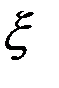= 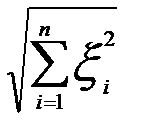, где( i = 1,2, …,n), 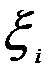= (y_i - y*_i), y_i - выходной параметр объекта.

Второе обстоятельство является в значительной мере следстви­ем требования универсальности моделей. Использование моделей клас­сов объектов или их элементов может приводить к неоднозначности оценки точности, поскольку в рамках класса характер проявления отдельных свойств объектов может колебаться в широких пределах, что в свою очередь сказывается на точности отображения этих свойств в модели. Таким образом, оценка точности подобных моде­лей может быть неоднозначной.

Третье обстоятельство обусловлено проблемой получения истин­ных значений параметров, с которыми сравниваются результаты моделирования. Чтобы получить эти значения необходимо провести с объектом эксперимент, погрешности которого не должны превышать ожидаемых потребностей математического моделирования. Однако это возможно далеко не всех случаях.

И, наконец, четвертое обстоятельство имеет место при статистическом моделировании случайных явлений или процессов. Здесь точность оценок вероятностей появления неко­торого события, среднего значения, дисперсий и других характери­стик случайных величин зависит от числа реализации процесса на модели и необходимой достоверности этих оценок. Например, при оценке вероятности р появления случайного события точность определяется по формуле

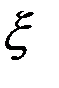= t 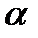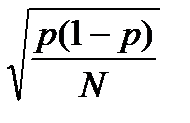, где t 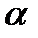- величина, зависящая от достоверности оценки, N = число реализаций модели.

Уменьшение необходимого числа реализации и, следовательно, затрат машинного времени достигается за счет целесообразного построения модели, в частности, выбором для оценки параметров случайных величин, имеющих возможно меньшую дисперсию.

Отметим, что в общем случае погрешности при моделировании зависят от ряда причин: неполного соответствия модели и объекта, неточности задания исходных параметров модели, случайного харак­тера результатов моделирования,

Вторым требованием является требование универсальности мате­матической модели, которое обусловлено большой трудоемкостью построения моделей. Поэтому с практической точки зрения окажется неприемлемым использование моделей, «настроенных» на узкий диапа­зон условий моделирования и требующих их существенной доработки при выходе за границы этого диапазона. В особенности это относит­ся к моделям элементов сложных систем, которые могут быть исполь­зованы в различных сочетаниях в соответствии со структурой моде­лируемой системы. Решение данной проблемы может лежать на пути создания некоторых универсальных схем в качестве моделей требуе­мого класса объектов. В пределе, при точной параметриза­ции объекта задание конкретной модели будет состоять в перечис­лении и задании параметров, полностью определяющих модель.

Требование экономичности математических моделей связано с необходимостью ограничить или минимизировать затраты машинного времени и памяти ЭВМ при использовании моделей. В качестве косвенного показателя экономичности может служить сложность модели, в частности, количество используемых параметров, количество внут­ренних связей и т.д. Экономичность зависит также от выбора языка программирования, эффективности использования стандартного программного обеспечения, общего построения программы. При статистическом моделировании сокращение числа реализации модели дости­гается, например, путем выбора оцениваемых параметров случайных величин и вероятностей случайных событий.

Отметим в заключение, что указанные требования в целом противоречивы. Например, с целью повышения экономичности модели, как правило, необходимо ее упрощение, однако подобное упрощение влечет за собой как невозможность получения отдельных характери­стик, так и появлением дополнительных погрешностей. И наоборот, желание получить универсальную и точную модель неизбежно ведет к ее усложнению, а следовательно, к росту объема вычислений и зани­маемой памяти ЭВМ. Построение моделей, в которых достигается при­емлемый баланс между всеми требованиями, производится обычно на основе эвристических принципов . Например, рекомендуется выбирать модель минимальной сложности при заданной точности, ли­бо максимальной точности при заданной сложности. Кроме того, рекомендуется соблюдать соразмерность погрешно­стей, вызываемых различными причинами.

Общие вопросы процесса построения модели и технология моделирования

Часто цитируют высказывание Эйнштейна о том, что правильная постановка задачи более важна, чем ее решение. Одному из класси­ков системного анализа Хитчу принадлежит такое высказывание: "Мой опыт показывает, что самые большие трудности для сис­темного аналитика не связаны с собственно аналитическими методами. Методы, которые мы в действительности используем в Министерстве обороны, обычно довольно просты и старомодны, Что отличает плодотворно работающего аналитика - это его способность... ставить проблему".

До последнего времени построение моделей считалось скорее искусством», чем процессом, поддающимся научно обоснованной регламентации. Процесс построения новой модели - это переход от эмпириче­ского описания, от гибкой (нечеткой) проблемной ситуации к четкой проблемной ситуации и к функциональной системе типа «вход-вы­ход».

При определении процедур этого перехода обратимся к классификации уровней знания, где вводятся следующие последовательные уровни знания:

1. Задан тип описания реальной системы.

2. Известна номенклатура входных и выходных характеристик.

3. Известны взаимосвязи входов и выходов.

4. Дополнительно к 1-3 известно начальное состояние системы до подачи входного воздействия.

5. Известны множество возможных состояний, функции измене­ния состояний и функции выхода.

6. Определены элементы системы и их взаимосвязь с характе­ристиками состояния, входа и выхода.

7. Полностью определена структура системы, включая взаимо­связи элементов между собой и с внешней средой. Заметим, что такая классификация уровней знания отражает по­следовательное "расширение" знании об объекте.

Сложность и многообразие реальных объектов - систем и процессов - обусловливают сложность процесса построения их математических моделей. Очевидно, не существует абсолютно универсальной во всех деталях схемы этого процесса, однако можно представить неко­торую общую агрегированную схему.

Рассмотрим содержание этапов подобной схемы применительно к задаче построения математической модели некоторого сложного процесса. По аналогичной схеме формируются и модели сложных систем.

Математическая модель является результатом формализации исследуемого процесса, т.е. построения формального (математическо­го) его описания. Однако для сложных процессов построение такого описания непосредственно по результатам наблюдения за процессом, оказывается невозможным. Формализации предшествует изучение процесса с целью выявле­ния присущих ему закономерностей и формулирования (или уточнения) постановки прикладной задачи. Результатом этого изучения являет­ся содержательное описание процесса. Содержательное описание несет исходную информацию, необходи­мую для выполнения последующих этапов - построения формализованной схемы и математической подели.

Содержательное описание составляется в словесной форме и включает сведения о физической природе процесса, его структуре, характеристиках отдельных элементарных явлениях. Эти сведения мо­гут быть получены двумя основными путями. Во-первых, путем прямых наблюдений процесса с фиксацией необходимых количественных харак­теристик в ходе экспериментов на реально существующем объекте (т.е, согласно приведенной ранее классификации, в результа­те "натурного моделирования"). Однако при разработке нового про­цесса на базе еще не существующих объектов, такая возможность от­сутствует. Отсюда следует другой путь составления содержательно­го описания, а именно использование накопленного опыта, анализ процессов функционирования аналогичных объектов, мысленное моде­лирование разрабатываемого процесса.

Обращаясь опять к классификации методов моделирования, можно сказать, что содержательное описание является по сути дела лингвистической моделью соответствующего процесса. Наряду с информацией относительно собственно исследуемого процесса, в содержательное описание входят также уточненная постановка прикладной задачи и необходимые для ее решения исходные данные.

Постановка прикладной задачи содержит: определение задач исследования, перечень искомых (выходных) величин и функций, требо­вания к точности их определения, состав факторов, которые должны учитываться при моделировании. В состав исходных данных включаются численные значения начальных условий, известных характеристик процесса.

Наличие содержательного описания позволяет перейти к разработке формализованнойсхемы моделируемого процесса, которая явля­ется промежуточным звеном между содержательным описанием и мате­матической моделью. Она составляется, как правило, для того, что­бы облегчить разработку математической модели. Формализованная схема, как и следует из ее названия, являет­ся уже строго формальным описанием моделируемого процесса. Для ее построения должны быть выбраны характеристики процесса, уста­новлена система параметров, определяющих процесс, достаточно стро­го определены зависимости между характеристиками и параметрами процесса с учетом факторов, учитываемых при формализации. На эта­пе построения формализованной схемы дается точная математическая формулировка задачи исследования с указанием окончательного переч­ня оцениваемых выходных величин и функций. Формализованная схема включает также систематизированный уточненный перечень исходных данных - известных параметров процесса и начальных условий. Эти величины представляются таблично или графически.

Например, проектируемый объект представляется в формализо­ванной схеме в виде некоторой системы S со многими векторными входами и выходами (Рис.6), имеющими следующий смысл:

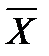- вектор входных (варьируемых) параметров, значения которых проектировщик имеет право изменять; в процес­се решения математической задачи для этих параметров должны быть найдены согласованные между собой опти­мальные значения;

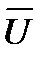- вектор входных (варьируемых) функций, графики кото­рых проектировщик имеет право изменять; в процессе решения математической задачи для этих функций долж­ны быть найдены согласованные между собой оптималь­ные зависимости;

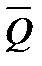- вектор входных (постоянных) параметров, значения ко­торых заданы проектировщику или физическими законами, или уровнем развития техники в современный ему проме­жуток времени, или решением задач более высокого уровня; 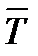- вектор входных (фиксированных) функций, происхождение которых объясняется причинами, указанными в описании вектора ;

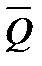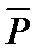- вектор входных (неуправляемых) параметров, значения которых могут изменяться случайным образом, незави­симо от желания проектировщика под влиянием неучтен­ных или неконтролируемых факторов;

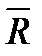- вектор входных (неуправляемых) функций, происхожде­ние которых объясняется причинами, упомянутыми в опиcании вектора ;

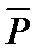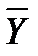- вектор выходных (критериальных) параметров, по зна­чениям которых оценивают качество проектируемого объекта;

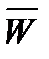- вектор выходных (критериальных) функций, по графикам которых оценивают качество процессов, происходящих в проектируемых динамических объектах. Если в качестве объекта рассмотреть вагон, то примерами компонент соответствующих векторов могут служить следующие пока­затели и характеристики:

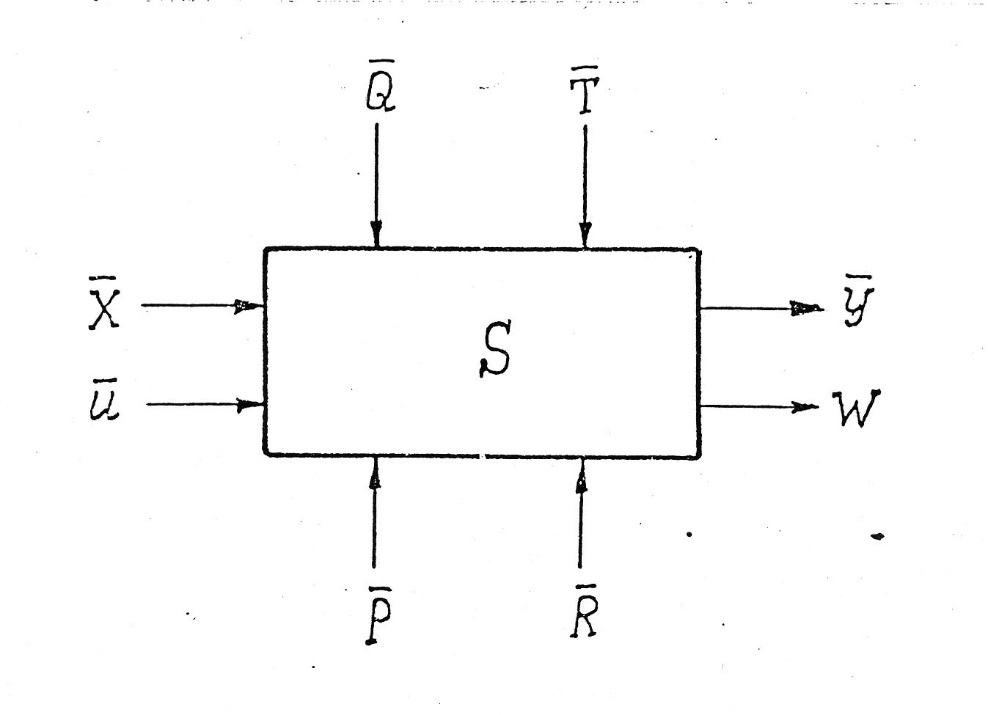
Рис. 6

Формализованную схему позволяет построить в большинстве случаев содержательное описание. Если же материал содержательного описания не дает оснований для точного описания каких-либо эле­ментов процесса, то могут потребоваться дополнительные эксперименты или наблюдения, позволяющие получить недостающую информацию.

Таким образом, формализованная схема подводит итог изучению моделиру­емого процесса, что дает возможность приступить к ее преобразо­ванию в математическую модель. Это преобразование проводится математическими методами на основании имеющейся информации о про­цессе. Оно предполагает запись в аналитической форме всех соотношений и составление систем неравенств для логических условий.

В приведенном выше примере результатом разработки зависимостей, связывающих каждую компоненту векторов выходных параметров 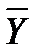и функций 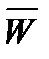с множеством соответствующих входных пара­метров и функций, является система, состоящая из двух векторных функционалов: 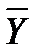= 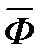₁ ( , , , , , , , ),

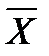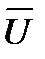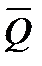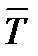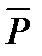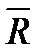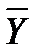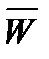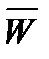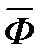= ₂( , , , , , , , ).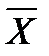

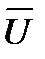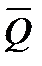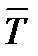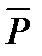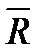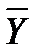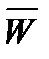Эта система является математической моделью объекта и описывает происходящие в объекте процессы в той мере, в которой это необходимо проектировщику. В результате проектировщик получает возможность в процессе оперирования с моделью получить ответы на вопросы ти­па: "Как изменятся выходные параметры Y_i и W_i при измене­нии варьируемых параметров X_m и U_n?", "На сколько улучша­ется параметр Y_m при улучшении на q_i характеристики q_i ?" и т.д.

Помимо указанных зависимостей при разработке математической модели, содержащиеся в формализованной схеме в виде таблиц и гра­фиков, исходные данные представляются в виде, удобном для вычисле­ний на ЭВМ. Так, эти таблицы и графики могут быть заменены интерполяционными полиномами, а для содержащихся в таблицах частот значений случайных величин подбираются аналитические выражения функций плотности законов распределений.

Подбор соответствующих аппроксимирующих выражений должен проводиться с учетом вносимых погрешностей. С методической точки зрения математиче­ская модель, строго говоря, в общем случае не полностью идентична формализованной схеме. Это обстоятельство является следствием ис­пользования приближенных зависимостей для представления данных, содержащихся в формализованной схеме, и может сказаться на совпадении результатов моделирования с экспериментальными данными. Заметим в связи с этим, что точность определения выхода за­висит от точности, с которой могут быть заданы входы и параметры моделируемого объекта и от степени соответствия модели реально­му объекту, т.е. от степени адекватности.

Понятно, что наиболее полным свидетельством адекватности модели является ее соответствие результатам работы ре­альной системы. Однако, математические модели, используемые в САПР, предназначены для прогноза поведения еще не существующей системы, и непосредственная полная проверка модели на адекват­ность в принципе невозможна. Поэтому возможна лишь косвенная про­верка, основанная на следующем.

Любая модель сложной системы базируется, на ряде более про­стых моделей элементарных процессов (объектов), которые хорошо изучены в прошлом, либо допускают простую экспериментальную про­верку (не обязательно путем простой постановки эксперимента, а, например, на основе сравнения результатов моделирования с реаль­ной статистикой).

Объединение простых элементов модели в более сложные сово­купности осуществляется с помощью некоторых правил дедукции следствий из гипотез, которые считаются обоснованными прошлым опытом, либо не противоречащими здравому смыслу, а сами правила логического вывода основаны на прошлом научном опыте в более широком смысле.

Более сложно обстоит дело с вопросом о том, какие элементы включать в модель, а какие считать несущественными. Единственным известным способом оценки существенности является моделирование фактора с последующим анализом чувствительности выхода по отноше­нию к вариациям характеристик. Если эти вариации несущественны, то элемент может быть исключен из модели. На практике нет возмож­ности проверить таким образом все элементы, и тогда оценка того, является ли элемент существенным, осуществляется на основе инженерного здравого смысла, а правильность выбора может быть прове­рена только последующими исследованиями и будущей практикой.