Математическая модель вагона как сложной механической системы
Построение математической модели сложной системы в целом часто оказывается практически невозможным из-за сложности процесса ее функционирования. В этих случаях, как упоминалось выше, приходится расчленять моделируемый объект на конечное число подсистем, сохраняя связи между подсистемами, обеспечивающих учет взаимодействия подсистем. Если получающиеся таким образом подсистемы все ещё сложны, расчленяют каждую из них (с сохранением связей) на конечное число более мелких подсистем. Процедуру расчленения подсистем продолжают до получения таких подсистем, которые в условиях рассматриваемой задачи будут признаны достаточно простыми и удобными для непосредственного математического описания. Эти подсистемы, не подлежащие дальнейшему расчленению, называются элементами сложной системы.
Таким образом, в общем случае сложная система является многоуровневой конструкцией из взаимодействующих элементов, объединяемых в подсистемы различных уровней.
Как мы уже отмечалось, представление моделируемого объекта в виде многоуровневой конструкции из элементов называется структуризацией объекта. В структурированной системе объектами материального мира являются только элементы и связи между ними. Объединение элементов в подсистемы - операция формальная, чисто структурная; она не вносит каких-либо новых объектов материального мира в совокупность элементов системы и связей между ними и не исключает имеющихся.
Математическая модель сложной системы состоит из математических моделей элементов и математической модели взаимодействия между элементами.
Рассмотрим способы объединения моделей элементов.
Наиболее общей формой модельного представления любого объекта является представление его в виде абстрактной системы по схеме «вход-выход». При этом система определяется как нечто, обладающее входами и выходами: входы - это совокупность воздействий на систему извне; выходы - совокупность воздействия со стороны системы вовне. Описание того, что происходит внутри этого «нечто», называется состоянием системы.
Чтобы задать (определить) систему необходимо:
- определить «входы»;
- определить состояния;
- детализировать «выходы»
- описать, как система меняет свое состояние - в терминах входов и текущего состояния.
Чтобы определить операцию, или эксперимент на системе, необходимо задать:
- начальное состояние системы;
- характер времени (дискретное, непрерывное) и рассматриваемые интервалы;
- воздействующие на систему «входы»;
- наблюдаемые «выходы».
Такого рода схемы «вход-выход» удобны для представления структуры модели: в качестве выходов при этом выступают те характеристики объекта, которые требуется определять при моделировании, а входами являются исходные параметры объекта, управления и возмущения.
Простейшим вариантом объединения систем является конъюнкция, когда системы функционируют независимо и имеют каждая свои входы и выходы (Рис.2)
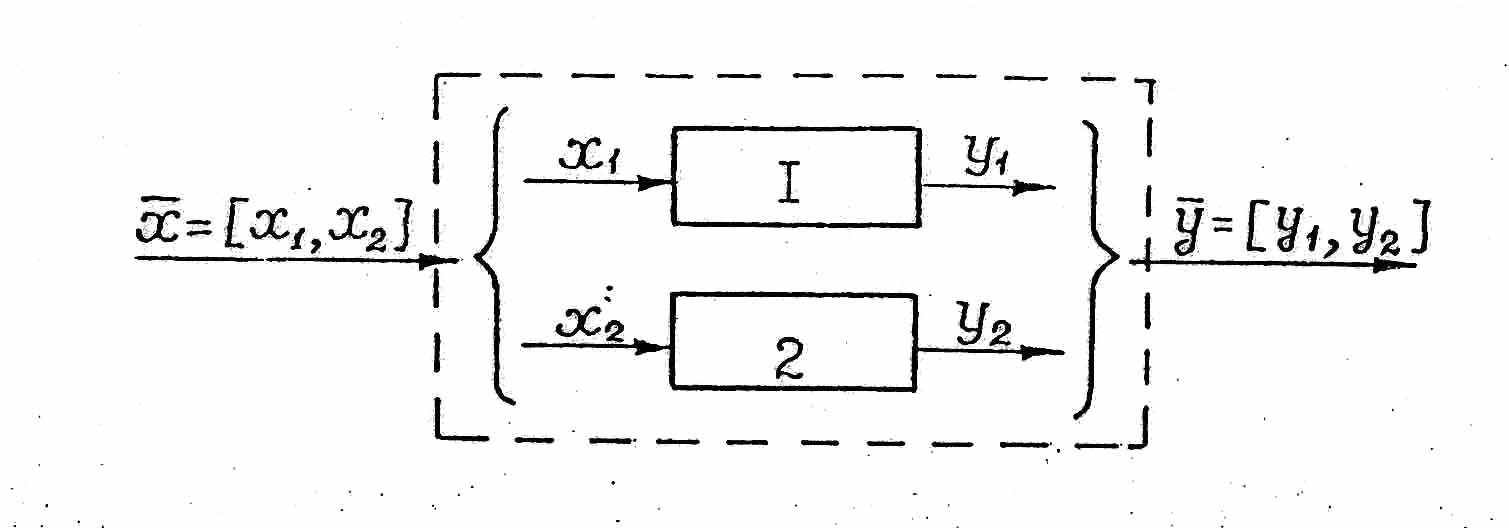
Рис.2
Другой способ - каскадное объединение, когда выход одной системы служит входом другой (рис. 3 ).
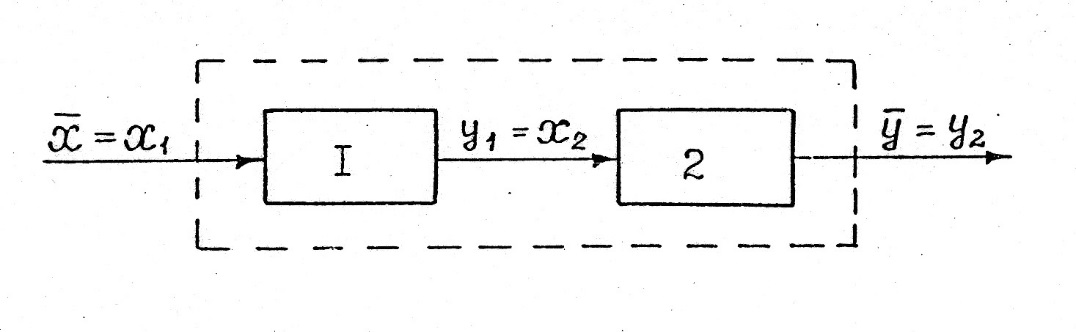
Рис.3
Еще  один способ - объединение с обратной связью. Здесь выход системы является одним из ее же входов (рис. 4 ).
один способ - объединение с обратной связью. Здесь выход системы является одним из ее же входов (рис. 4 ).
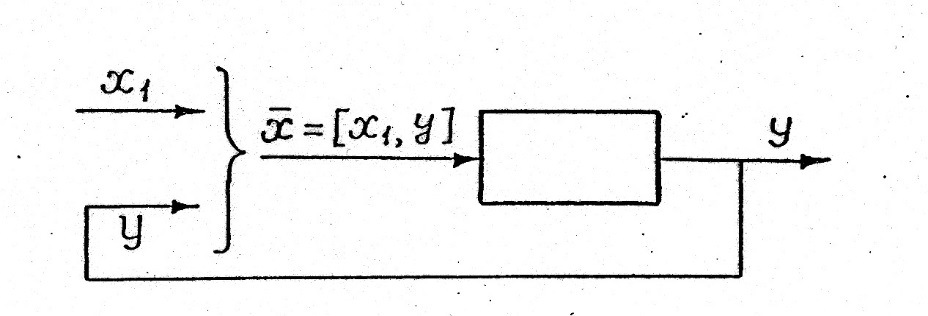
Рис.4
Все другие возможные варианты являются комбинацией этих трех элементарных способов объединения.
Пусть имеется математическая модель, которая позволяет оценить максимальное количество Р пассажиров, ежедневно доставляемых на некоторое фиксированное расстояние, в зависимости от технико-эксплуатационных характеристик (ТЭХ) и затрат на программу производства пассажирских поездов одного типа. В виде схемы входа-выхода эту модель можно изобразить в виде:
| P(t) |
| Модель программы |
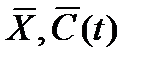
|
Здесь 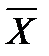 - вектор ТЭХ,
- вектор ТЭХ, 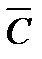 (t)= [Сс(t), Сп(t), Сэ(t)] - ассигнования на реализацию программы создания и эксплуатации парка вагонов в функции времениt, представленные по таким видам затрат, как затраты на НИОКР (Сс), серийное производство (Сп) и эксплуатация (Сэ).
(t)= [Сс(t), Сп(t), Сэ(t)] - ассигнования на реализацию программы создания и эксплуатации парка вагонов в функции времениt, представленные по таким видам затрат, как затраты на НИОКР (Сс), серийное производство (Сп) и эксплуатация (Сэ).
Пусть далее модель, состоит из блоков: блок функционирования парка численностью n вагонов, блок оценки длительности НИОКР и блок серийного производства. Тогда эта блочная модель может изображаться следующим образом (рис. 5 ).
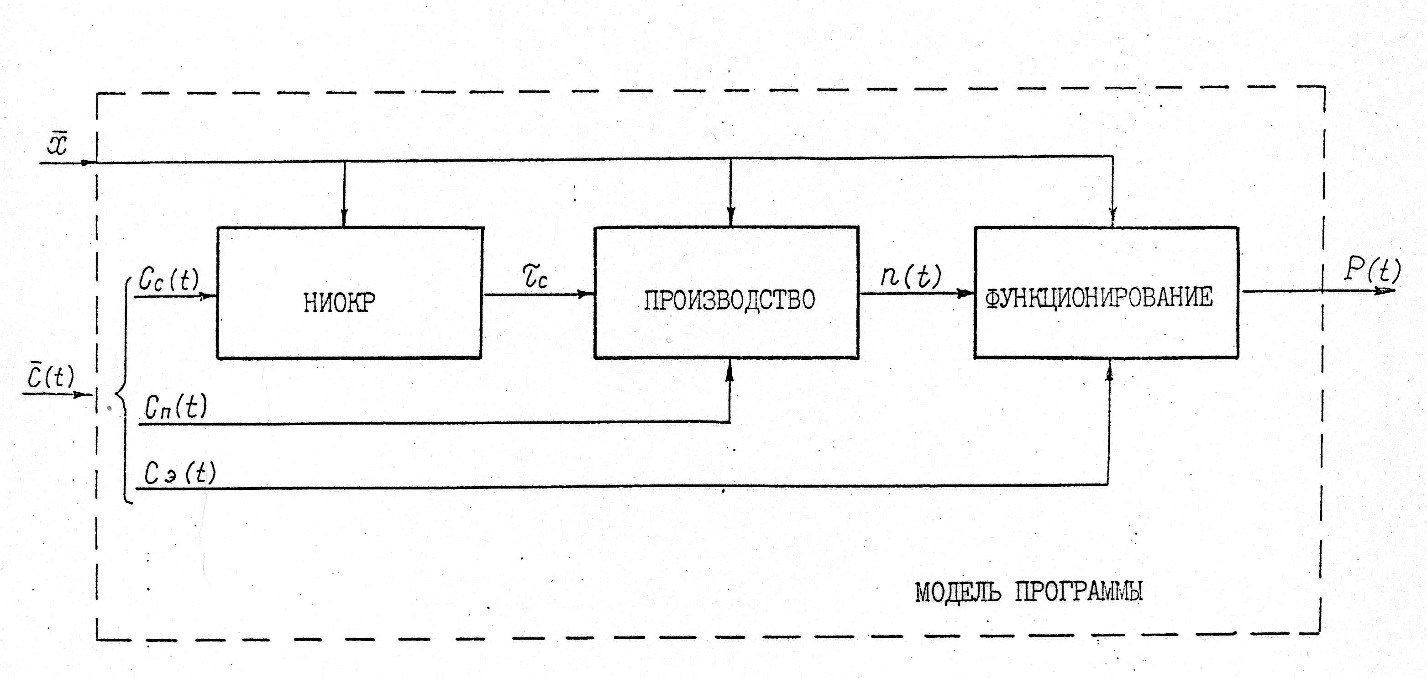
Рис.5 Схема модели программы пассажирских вагонов
Все сказанное о схемах «вход-выход» полностью относится и к этой схеме модели программы пассажирских вагонов. В частности, моделирование как операция на абстрактной системе задается следующими элементами: определение начального состояния, определение масштаба и интервалов времени, определение входов 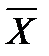 и
и 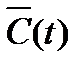 , и как результат - определение выхода P(t).
, и как результат - определение выхода P(t).
Поскольку мы обсуждаем математические модели, то каждый из трех изображенных блоков должен быть реализован в виде математических соотношений или алгоритмов пересчета входных характеристик в выходные. Значит, каждый j-ый блок модели воспроизводит оператор преобразования входных характеристик Xj в выходные Yj
Yj(t) = Lj [ Xj(t)], j=1,2,..N
Yj = [Yj1, Yj2, ….. Yjk, …… YjK], k = k(j); X(j) = [Xj1, Xj2, ……. Xjq ….. XjQ] , q = q(j).
Совокупность блоков отображает набор L операторов преобразования Lj и условий объединения входов и выходов блоков типа
Xjq(t) = Yjk(t), где j Î [1,N], q(j) Î [1, Q], k(j) Î [1, K]
Эти формальные условия, в зависимости от конкретной формы их записи, могут отражать конкретные способы объединения элементарных блоков.
Дата добавления: 2015-12-16; просмотров: 1110;
