Сущность метода конечных элементов
Вводные замечания.
Пусть поведение искомой функции U(x, y, z) внутри заданной ограниченной области W с границей ¶W описывается некоторым дифференциальным уравнением 2m - го порядка
L(2m)(U, k, x, y, z) = q (x, y, z) (1)
где q(x, y, z) внешнее воздействие, к - параметр, обобщенно характеризующий свойства сплошной cреды в объеме W(омега).
Уравнение (1) дополняется совокупностью m - краевых условий на поверхности, ограничивающей область W ;
а) главных, куда входят производные от искомой функции по координатам не выше (m-1) - го порядка.
Г i (U, ..., 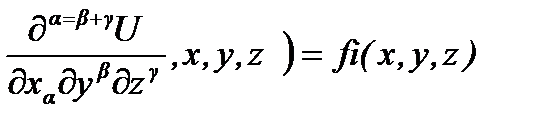 (2)
(2)
(1£ a+b+g £ m-1; i=1,...,r )
б)естественных, уравнения которых содержат хотя бы один член с производной порядка a+b+g ³ m ;
Et(U,..., 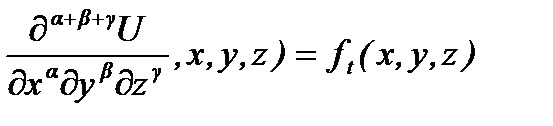 (3)
(3)
(m £ (a+b+g )max < 2m-1; t= r+1,...m)
В строительной механике главные краевые условия называют кинематическими, а естественные - силовыми граничными условиями. Известно, что во многих задачах механики сплошных сред для определения функции U(x, y, z) вместо совместного рассмотрения уравнения (1) и краевых условий (2) и (3) можно использовать условие стационарности некоторого функционала
d Э(U) = 0.
Функционал Э(U) содержит производные от U(x, y, z) до m-го порядка (вместо 2m в уравнении (1)). Это облегчает подбор аппроксимирующих функций для U(x, y, z), поскольку для получения однозначного значения функционала Э(U) требуется обеспечить непрерывность функции U(x, y, z) и ее производных лишь до (m-1)-го порядка включительно. Мы перечисли основные операции в алгоритме МКЭ. Рассмотрим их подробнее.
9.2. Идеализация области W (разбиение на элементы)
В области W фиксируется некоторое конечное число узловых точек. На множество узловых точек наносится сетка разбиения области на конечное число подобластей (элементов). Ихсборка образует модель всей области.
Выбор размеров, формы и числа узловых точек для конечных элементов зависит от характера рассматриваемой задачи, вида исходной области, градиента самой искомой функции и других факторов, которые, в конечном счете, определяют точность решения задачи. Например, при решении плоских задач (плоское напряженное состояние, обтекание тел потоком жидкости, задача теплопроводности в пластине и т.д.) область аппроксимируется треугольными, четырехугольными и плоскими элементами. Если рассматривается трехмерная область, то она обычно идеализируется с помощью элементарных тетраэдров, прямоугольных параллелепипедов либо неправильных шестигранников.
К сказанному добавим, что замена исходной конструкции совокупностью конечных элементов подразумевает равенство энергий конструкции и её дискретной модели. Для некоторых конструкций соблюдение энергетического баланса ведёт к получению дискретной модели, точно описывающей поведение исходной конструкции. Это характерно для конструкций, которые уже состоят из отдельных элементов с дискретным сочленением между ними, например, ферм, рам, стержневых конструкций. Если же элементы реальной конструкции имеют вдоль своей границы непрерывные связи со смежными элементами, то при построении дискретной модели следует вводить некоторые предположения о характере силового или кинематического взаимодействия между смежными элементами. В этом случае дискретная модель будет лишь приближенно отражать поведение исходной конструкции.
9.3. Выбор основных неизвестных.
В качестве основных неизвестных в МКЭ принимаются узловые значения искомой функции и её частных производных до m - го порядка. Правда, для обеспечения условий сходимости метода достаточно включить в число неизвестных лишь определенную часть из общего числа производных m - го порядка. Кроме того иногда производные m - го порядка полностью исключаются из числа узловых неизвестных. Например, при решении задач, описываемых квазигармоническим уравнением (2m = 2) типа
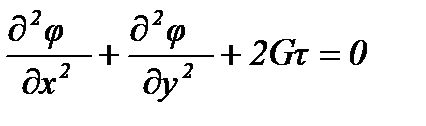
(квазигармоническим уравнением, дополненным условиями на границе описываются кручение призматических стержней, теплопроводность, гравитация, волновые процессы, гидродинамика жидкости).
В качестве неизвестной в каждой i -ой узловой точке достаточно принять значение определяемой функции Ui. Если же рассматривается более сложная задача для плоской области, описываемая бигармоническим уравнением (2m = 4)
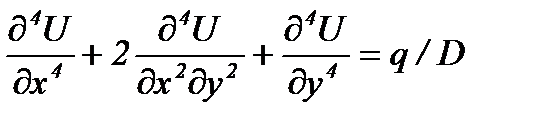 , то для строгого соблюдения условий сходимости метода в каждой узловой точке следует уже принять в качестве неизвестных
, то для строгого соблюдения условий сходимости метода в каждой узловой точке следует уже принять в качестве неизвестных
Ui, 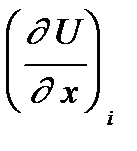 ,
, 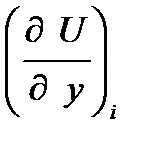
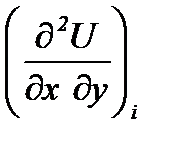
Общее число неизвестных для конечного элемента определяется числом его степеней свободы, от которого зависит точность описания искомой функции в объёме каждого из конечных элементов, а следовательно и во всей области W. Повысить точность решения можно либо путем увеличения числа конечных элементов, либо путём увеличения числа свободы для каждого из конечных элементов.
Например:
9.4. Построение интерполирующего полинома.
Это одна из основных операций метода - построение интерполирующего полинома, которым аппроксимируется искомая функция U(x,y,z) в объёме конечного элемента: коэффициенты в этом полиноме выражаются через значения узловых неизвестных элемента.
Основная трудность состоит в том, что полиномы для каждого из конечных элементов должны обеспечить непрерывность функции U(x,y,z) и её производных до (m-1)- го порядка включительно по всей области W.
Что же касается производных m - го порядка, то в каждом из интерполирующих полиномов должны сдержаться члены, обеспечивающие их переход к постоянным значениям при уменьшении размеров конечного элемента. При этом производные m - го порядка могут иметь разрывы первого рода по граням стыковки смежных конечных элементов. После соблюдения этих условий построения интерполирующих полиномов можно, определяя значения функционала Э(U) для всей области W, воспользоваться зависимостью
Э(U)= 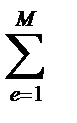 Эe(U) (2)
Эe(U) (2)
где Эe(U) - значение функционала Э(U) в замкнутом объёме e - го
конечного элемента;
Предположим, что интерполирующий полином может быть представлен для e- го конечного элемента в виде:
U(e) (x,y,z) = 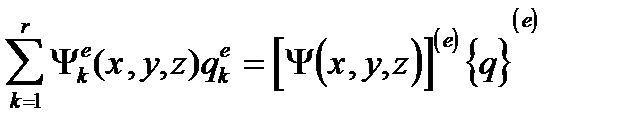
где {q }(e) - вектор-столбец, состоящий из r узловых неизвестных e- го конечного элемента;
[y(x,y,z)] 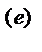 - вектор-строка, элементами которого являются известные функции координат точек yk(e)(x,y,z). Вид этих функций определяется геометрией элемента, классом задач и содержанием вектора {q}(e).
- вектор-строка, элементами которого являются известные функции координат точек yk(e)(x,y,z). Вид этих функций определяется геометрией элемента, классом задач и содержанием вектора {q}(e).
Тогда аппроксимация функции U(x, y, z), определится суммой:
U(x, y, z)= 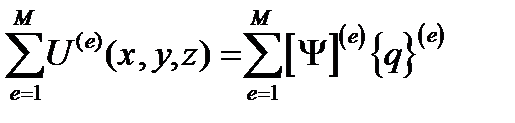
или U(x, y, z)=[ y(x,y,z)]{q} ,
где [ y(x,y,z)]=[[y] 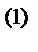 [y]
[y] 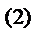
 ... [y]
... [y] 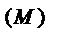 ]
]
{q}={{q} 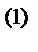 {q}
{q} 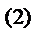 ... {q}
... {q} 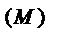 }
}
есть вектор узловых неизвестных для полной области в местной системе координат.
Внося в функционал Э(U) в последнее выражение для U(x, y, z) получим некоторую определённую функцию узловых неизвестных Э(q).
Построенные в локальных подобластях аппроксимации функции обеспечивают непрерывность функции U(x, y, z) и её производных до (m-1)- го порядка во всей области (при том, что производные m-го порядка могут иметь разрывы первого рода на гранях стыковки смежных конечных элементов). Это обеспечивает сходимость решения по МКЭ к точному при уменьшении размеров конечных элементов. Естественно, что при выбранной геометрии подобласти для обеспечения условий сходимости нужно располагать в интерполирующей функции достаточным количеством произвольных параметров. Дальнейшее увеличение числа произвольных параметров в интерполирующей функции связано с необходимостью введения дополнительных узловых неизвестных и дополнительных узловых точек подобласти. В результате получаются так называемые высокоточные конечные элементы. В качестве узловых неизвестных принимаются значения искомой функции и её производных до (m-1) -го порядка. При этом необходимое число неизвестных в основных узловых точках следует набирать, последовательно переходя от функции к производным возрастающего порядка. Исключение из числа узловых неизвестных какой - либо производной порядка ниже, чем (m-1) может привести к нарушению сходимости решения по МКЭ к точному.
Одномерная область.
Пусть замкнутый интервал [ 0,l ] изменения x разбит внутренними точками:
0= x0 < x1 < x2 < ... < xl-1 < xl < ... < xm-1 < xm = l (1)
на ряд замкнутых участков - элементов
[x0,x1], [x1,x2], ... , [xl-1,xl], ... , [xm-1,xm], (2)
Искомую функцию U(x) в e-oм элементе аппроксимируем полиномом n-ой степени: U 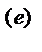 @
@ 
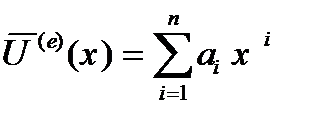 , где xÎ[ xl-1, xl] (e=1,2,....,M) (3)
, где xÎ[ xl-1, xl] (e=1,2,....,M) (3)
Доказано, что непрерывность функции U(x) и ее производных до m-1 -гопорядка в интервале [ 0,l ] обеспечена, если степень каждого из полиномов 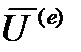 удовлетворяет условию:
удовлетворяет условию:
n ³ 2m-1 (4)
и для определения неизвестных параметров ai среди (n+ 1) -го условия для каждого e - го участка содержатся следующие условия:
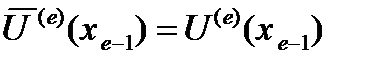 ;
; 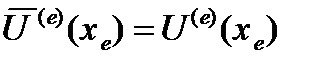
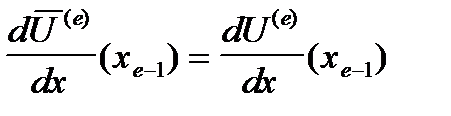 ;
; 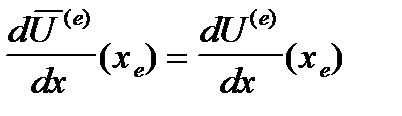 ; (5)
; (5)
........................................................................................................
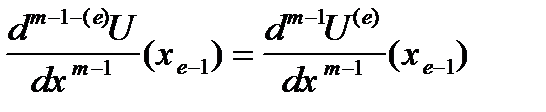 ;
; 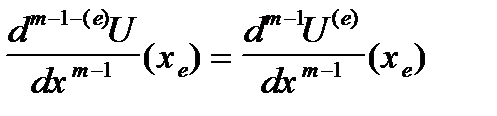 ;
;
При n > 2m-1 недостающие для нахождения параметров ai условия составляются по аналогии с (5), но лишь для некоторых промежуточных узловых точек. Если для e-го элемента выбрана не одна, а несколько промежуточных точек, то не обязательно в каждой из них требовать выполнения одних и тех же условий. Важно лишь в каждой из точек не допускать пропуска условий по производным промежуточных порядков. В дальнейшем ограничимся рассмотрением простейших одномерных конечных элементов с расположением узловых точек лишь по его концам. Для таких элементов степень интерполирующего полинома n определяется из равенства:
n=2m-1
Пример 1. Для одномерной краевой задачи, описываемой дифференциальным уравнением второго порядка (2m=2), построить интерполирующий полином для e- го конечного элемента. Заметим, что уравнением такого типа описываются некоторые из задач растяжения и кручения стержней, одномерные задачи теплопроводности, гравитации, гидромеханики.
Решение. n = 2m-1=1
Следовательно, интерполирующий полином будет иметь вид:`
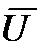 (x)=ao+a1x
(x)=ao+a1x
Неизвестные ао и а1 определим из (5), которые для2m=2дают два условия:
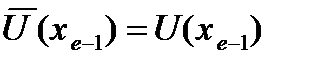 ;
; 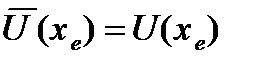 ;
;
Отсюда: ао+ a i (x 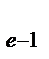 ) = U (x
) = U (x 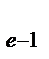 ); ао+ a i (x
); ао+ a i (x 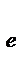 ) = U (x
) = U (x 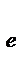 );
);
a i = 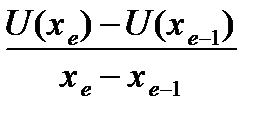
a o = 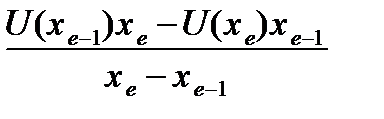
Тогда получим формулу для интерполирующего полинома:
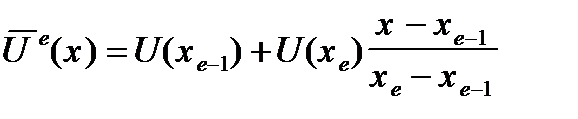
Пусть для определенности интервал изменения х разбит на четыре конечных элемента
| x |
| x1 |
| x2 |
| x3 |
| x4 |
| x0=0 |
| x1 |
| x2 |
| x3 |
| x4= l |
| x |
| x |
| x |
| x |
| x |
| x |
| x |
| U(xo) |
| U(x1) |
| U(x2) |
| U(x3) |
| U(x4) |
| U(x) |
| j0(x) |
| j1(x) |
| j2(x) |
| j3(x) |
| j4(x) |
| x1 |
| x2 |
| x3 |
| x4 |
| x1 |
| x2 |
| x3 |
| x4 |
| x1 |
| x2 |
| x3 |
| x4 |
| x1 |
| x2 |
| x3 |
| x4 |
| x1 |
| x2 |
| x3 |
| x4 |
Тогда , склеивая интерполирующие полиномы по отдельным элементам, получим аппроксимирующую функцию U(x) для всей области.
Функцию U(x) можно представить в виде суммы:
U(x)= 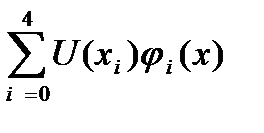
Отсюда видна локальность координатных функций j i (x), каждая из которых оказывается отличной от нуля лишь в области конечных элементов, непосредственно примыкающих к данному узлу.
Это свойство координатных функций МКЭ позволяет как бы набирать искомое решение из отдельных ²универсальных кирпичиков². Именно в этом - одно из основных достоинств МКЭ.
Пример 2. Для одномерной краевой задачи, описываемой дифференциальным уравнением 4-го порядка (2m=4), следует построить интерполирующий полином для конечного элемента. К этому классу задач относится задача изгиба балок.
Решение. n=2m-1=3
Следовательно, интерполирующий полином имеет вид:
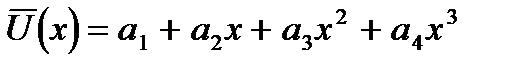 (1)
(1)
Значительно проще строить выражение для интерполирующего полинома не в общей, связанной со всей областью, системе координат, а в местной, связанной с рассматриваемым конечным элементом.
| l |
| y |
| x |
| Обозначим длину конечного элемента через l . (На рисунке положительные направления сил 1 и 3 и моментов 2 и 4 ). |
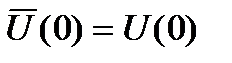 ;
; 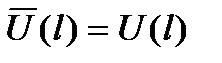 ;
;
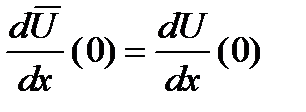 ;
; 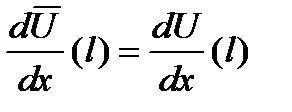
Введем для узловых значений функции u(x) обозначения
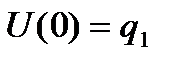 ;
; 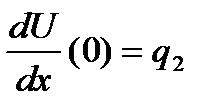 ; U(l)=q3;
; U(l)=q3; 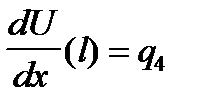 ;
;
На рисунке указаны положительные значения величин. С учетом этих обозначений, получаем:
a1 = q1 a1+a2 l+a3 l 2+a4 l 3= q3
a2 = q2 a2+ 2a3 l+3a4 l 2= q4
откуда:
a1 = q1 a3= 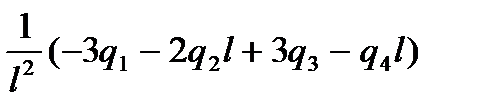
a2 = q2 a4= 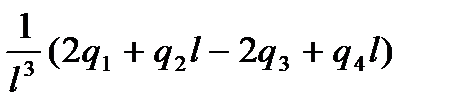
Подставляя найденные значения параметров a i в (1) можно получить для интерполирующего полинома выражение:
U(x)= 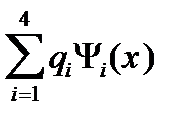
где 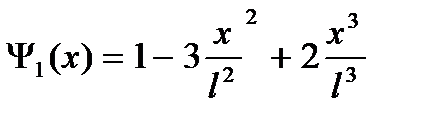 ;
; 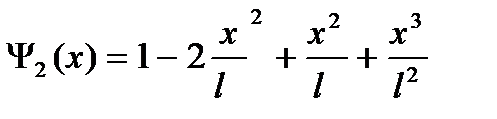 ;
;
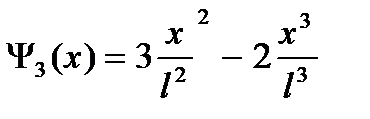 ;
; 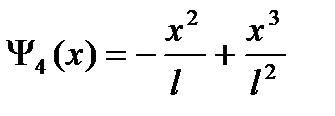 ;
;
так называемые одномерные функции формы ( в теории аппроксимации - функции Эрмита), удовлетворяющие следующим свойствам:
y1(0)=1; y1’(0)=0; y1(l)=0; y1’(l)=0; Графики этих функций
y2(0)=0; y2’(0)=1; y2(l)=0; y2’(l)=0; в пределах конечного
y3(0)=0; y3’(0)=0; y3(l)=1; y3’(l)=0; элемента представлены
y4(0)=0; y4’(0)=0; y4(l)=0; y4’(l)=1; ниже :
| y4(x) |
| y3(x) |
| y1(x) |
| y2(x) |
| x |
| x |
| x |
| x |
| x |
| x |
| x |
| x |
| x |
| x |
| x |
| j1(x) |
| j2(x) |
| j3(x) |
| j4(x) |
| j5(x) |
| j6(x) |
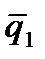
|
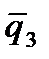
|
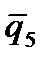
|
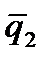
|
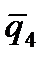
|
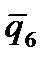
|
| j1(0)=1 |
| j‘2(0)=1 |
| j3(x1)=1 |
| j‘4(x1)=1 |
| j‘6(x2)=1 |
| j5(x2)=1 |
| x1 |
| x2 |
U(x)= 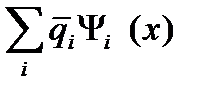 Вид координатных функций для одномерной области, разбитой на два элемента.
Здесь через
Вид координатных функций для одномерной области, разбитой на два элемента.
Здесь через 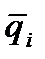 обозначены узловые неизвестные для всей области (или в общей системе координат) обозначены узловые неизвестные для всей области (или в общей системе координат)
|
| Располагая выражениями для интерполирующих полиномов каждого из конечных элементов рассматриваемой области можно представить для аппроксимирующей функции U(x) в виде суммы произведения узловых неизвестных на соответствующие координатные функции. |
.Двумерная область. Прямоугольный элемент.
Пусть некоторая двумерная область W, отнесенная к системе осей OXY,
представлена в виде совокупности конечных прямоугольных элементов
wK(к =1,2,....М). Стороны каждого элемента параллельны осям ОХ и ОY. Искомую функцию U(x,y) в границе e -го элемента представим в виде полинома:
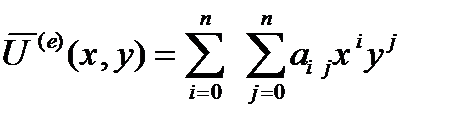 (1)
(1)
являющегося произведением двух ортогональных одномерных полиномов. Общее число неизвестных коэффициентов ai j равно (n+1)2. Доказано, что если среди (n+1)2 условий для определения коэффициентов ai j полинома (1) присутствуют 4m2 следующих условий:
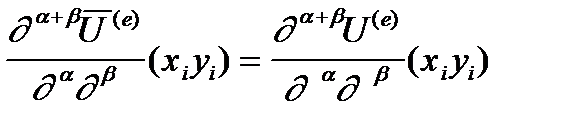 (2)
(2)
(a, b=0, 1, ..., m-1), ( i = 1, 2, 3, 4 )
то получаемые при этом аппроксимирующие функции 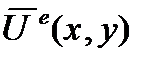 обеспечивают
обеспечивают
непрерывность функции 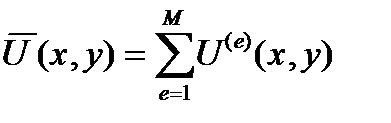 и ее производных до (m-1)- го порядка во всей области W.
и ее производных до (m-1)- го порядка во всей области W.
Отсюда следует, что минимальное число неизвестных, при котором оказывается выполненными условия сходимости метода, равно: r =(n+1)2 = 4m2
Если же число r = (n+1)2 > 4m2 то 4m2 условий необходимо дополнить аналогичными условиями, но выписанными для некоторых других узловых точек, расположенных, например, посередине каждой из строк прямоугольного элемента.
Пример 3. Для двумерной задачи, описываемой дифференциальным уравнение
второго порядка (2m=2), построить интерполирующий полином.
Решение. Число узловых неизвестных r = 4m2 = 4
а показатель степени полинома n = 2m-1 = 1.
Следовательно интерполирующий полином должен иметь вид:
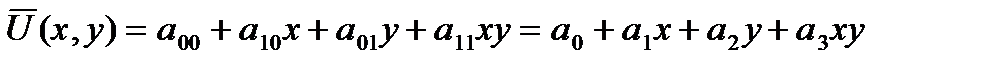 (3)
(3)
Неизвестные коэффициенты a i определяются из условий (2), которые в данном случае принимают вид:
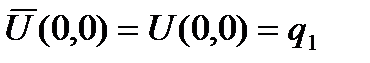
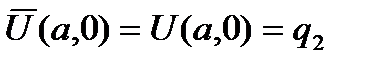
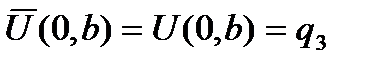
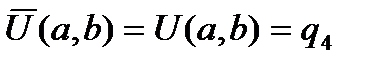
С учетом (3) система получается такой:
a0 = q1 a0 + a1 a = q2
a0 + a2b = q3 a0 + a1 a + a2 b + a3 ab = q4
Подставляя a i , найденные из последней системы, получаем для интерполирующего полинома в границах конечного элемента выражение вида:
U(x,y)= 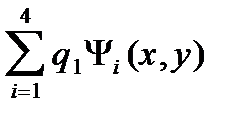
где 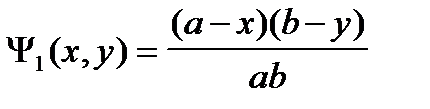 ;
; 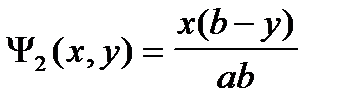 ;
;
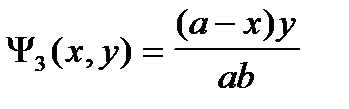 ;
; 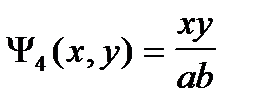 .
.
Пример 4. Построить интерполирующий полином для краевой задачи, описываемой дифференциальными уравнениями четвертого порядка ( 2m = 4 ).
Решение. Число узловых точек r = 4 m2 = 16, а показатель степени полинома
n = 2m-1 = 3. Следовательно интерполирующий полином для функции U(x,y) должен иметь вид:
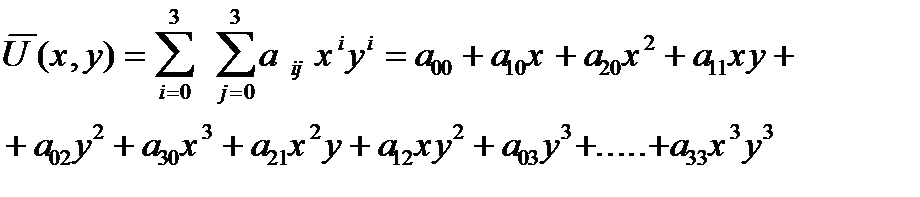
Для определения 16 неизвестных коэффициентов в каждой из четырех узловых точек прямоугольного элемента нужно составить по четыре условия типа:
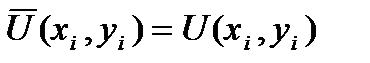
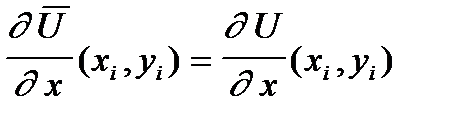
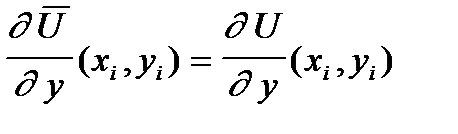
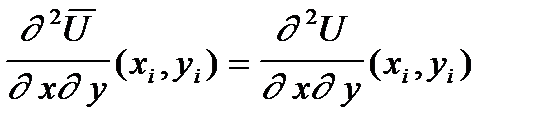 i = 1,2,3,4
i = 1,2,3,4
Подстановка выражения для 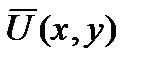 в эту систему приводит к системе 16 алгебраических уравнений относительно коэффициентов a i j через узловые значения искомой функции U(x,y) и ее производные
в эту систему приводит к системе 16 алгебраических уравнений относительно коэффициентов a i j через узловые значения искомой функции U(x,y) и ее производные 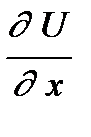 ,
, 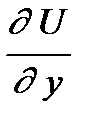 ,
, 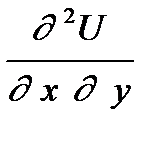 , которые в МКЭ принимаются в качестве основных неизвестных. Внося полученные a ij в выражение для
, которые в МКЭ принимаются в качестве основных неизвестных. Внося полученные a ij в выражение для 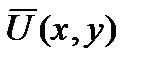 получаем интерполирующий полином.
получаем интерполирующий полином.
Дата добавления: 2015-12-16; просмотров: 1257;
