Получение основной системы разрешающих уравнений.
Минимизируя функцию Э(q) по всем элементам вектора [q]всей области, получаем:
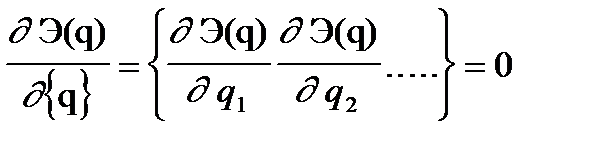
Учитывая, что Э(U) = 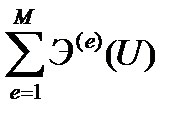
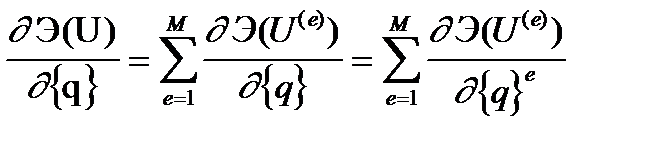 (3)
(3)
где суммирование производится по всем конечным элементам.
Для линейных задач функционал Э(U) является квадратичной функцией от U и ее производных, и следовательно, e-ый член правой части (3) принимает вид:
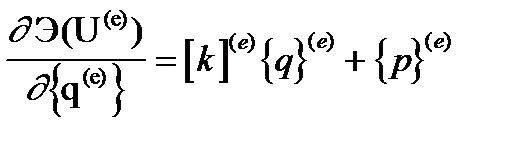 (4)
(4)
где [k]( e ) - квадратная матрица размером r ´ r
( r - число узловых неизвестных e -го элемента)
Коэффициенты этой матрицы определяются свойствами среды. Для нелинейных задач матрица [k](e ) является функцией вектора {q(e)} - вектор узловых неизвестных.
Вектор {p(e)} имеет размер r , он характеризует внешнее воздействие на
e-ый элемент. С учетом (4) уравнение можно переписать:
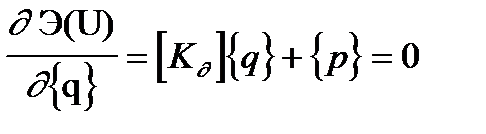 (5)
(5)
где [K¶]= 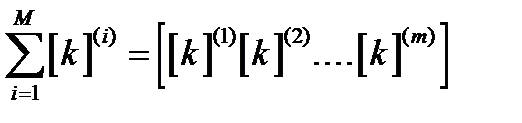 - квазидиагональная матрица порядка r ´ M (М - число элементов),
- квазидиагональная матрица порядка r ´ M (М - число элементов),
{p} = { {p}(1) {p}(2) .....{p}(m)} - вектор размером r ´ M.
Уравнение (5) записано в местной системе координат. В целях дальнейших упрощений целесообразно от местной системы осуществить переход к так называемой общей системе координат.
Введем для S - ой узловой точки вектор неизвестных 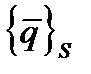
Совокупности этих векторов образуют вектор основных неизвестных в общей системе координат
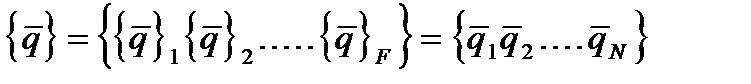
где F - число узлов, N - число неизвестных по всей области.
Между векторами {q} и 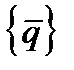 существует некоторая связь
существует некоторая связь
{q}= [Н] 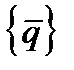
где [Н] - булева матрица размером M ´ N . Ее структура определяется геометрией элемента, классом краевой задачи и принятым порядком нумерации для элементов векторов {q} и 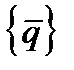 .
.
Если принять в векторе {р}(e) тот же порядок нумерации компонентов, что и в векторе {q}(e) , то умножив (5) на матрицу [H] T , с учетом зависимости (6), получим:
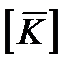
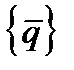 +
+ 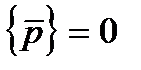 (7)
(7)
где 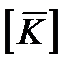 = [ H ]T [К¶] [ H ] - общая матрица коэффициентов при основных неизвестных в общей системе координат для всей области.
= [ H ]T [К¶] [ H ] - общая матрица коэффициентов при основных неизвестных в общей системе координат для всей области.
Размер квадратной матрицы 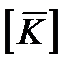 равен N ´ N .
равен N ´ N .
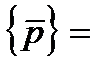 [ H ]T
[ H ]T 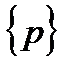 - вектор-столбец размером N . Его элементы характеризует внешнее воздействие на всю область W. Полученное матричное уравнение (7) и есть искомая система алгебраических уравнений для определения основных узловых неизвестных
- вектор-столбец размером N . Его элементы характеризует внешнее воздействие на всю область W. Полученное матричное уравнение (7) и есть искомая система алгебраических уравнений для определения основных узловых неизвестных 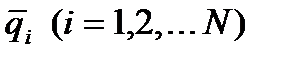 .
.
Дата добавления: 2015-12-16; просмотров: 720;
