Лекция 17. Тонкая структура термов. Лэмбовский сдвиг
Атом водорода
Для атома водорода 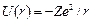 , где r –расстояние между ядром и электроном. В сферической системе координат уравнение Шредингера:
, где r –расстояние между ядром и электроном. В сферической системе координат уравнение Шредингера:
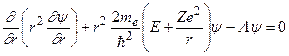 , (3.3)
, (3.3)
где  – оператор Лежандра. Ядро считается неподвижным. Чтобы учесть его движение, нужно заменить массу электрона на приведенную массу.
– оператор Лежандра. Ядро считается неподвижным. Чтобы учесть его движение, нужно заменить массу электрона на приведенную массу.
Уравнение (3.3) решается по методу разделения переменных:
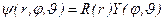 . (3.3а)
. (3.3а)
Из (3.3) следует:
 , (3.4)
, (3.4)
где  – постоянная разделения. Приходим к независимым уравнениям для угловой части Y и радиальной части R волновой функции:
– постоянная разделения. Приходим к независимым уравнениям для угловой части Y и радиальной части R волновой функции:
 , (3.5)
, (3.5)
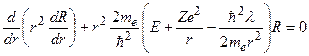 . (3.6)
. (3.6)
Постоянная разделения  , где
, где 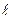 – орбитальное квантовое число. В уравнении (3.6) сумма электростатической и центробежной энергий играет роль эффективной потенциальной энергии (рис.3.1):
– орбитальное квантовое число. В уравнении (3.6) сумма электростатической и центробежной энергий играет роль эффективной потенциальной энергии (рис.3.1):  . (3.7)
. (3.7)
Потенциальная энергия имеет «яму» с минимальным значением на расстоянии
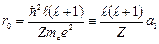 , (3.7a)
, (3.7a)
где  – радиус первой боровской орбиты. Глубина «ямы»:
– радиус первой боровской орбиты. Глубина «ямы»:
 ,(3.7б)
,(3.7б)  энергия основного состояния водорода.
энергия основного состояния водорода.
 Если энергия частицы положительна (
Если энергия частицы положительна (  ), то ее движение инфинитно. Если энергия отрицательна (
), то ее движение инфинитно. Если энергия отрицательна (  ), то частица находится в потенциальной яме (финитно). Рассмотрим далее решение уравнения (3.6) при отрицательных значениях энергии. Введем безразмерные переменные:
), то частица находится в потенциальной яме (финитно). Рассмотрим далее решение уравнения (3.6) при отрицательных значениях энергии. Введем безразмерные переменные:
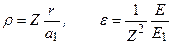 . (3.8)
. (3.8)
Решение ищется в виде:
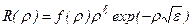 , (3.9)
, (3.9)
Рис.3.1 Функция 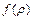 удовлетворяет уравнению:
удовлетворяет уравнению:
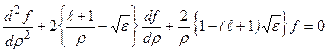 . (3.10)
. (3.10)
Решение ищется в виде бесконечного ряда
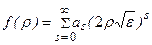 . (3.11)
. (3.11)
Можно получить рекуррентное соотношение
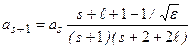 . (3.11а)
. (3.11а)
Ряд (3.11) с коэффициентами (3.11а) расходится быстрее, чем 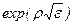 . Естественное условие будет удовлетворяться, если функцию
. Естественное условие будет удовлетворяться, если функцию 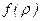 рассматривать в виде полинома некоторой степени
рассматривать в виде полинома некоторой степени 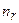 . Ряд (3.11) становится полиномом степени
. Ряд (3.11) становится полиномом степени  при условии
при условии 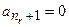 :
:
 . (3.12)
. (3.12)
Это условие определяет собственные значения энергии водородоподобного атома:
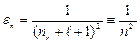 . (3.12а)
. (3.12а)
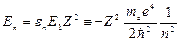 . (3.13)
. (3.13)
Это – в точности формула Бора.
Число 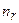 - радиальное квантовое число, главное квантовое число:
- радиальное квантовое число, главное квантовое число:
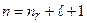 . (3.13a)
. (3.13a)
При фиксированном числе n орбитальное квантовое число принимает n значений от 0 до n – 1:
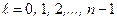 . (3.14)
. (3.14)
Радиальная волновая функция (3.9) зависит от квантовых чисел 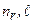 . Удобнее пользоваться набором n,
. Удобнее пользоваться набором n, 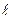 . Стационарные состояния водородоподобного атома описываются волновыми функциями (3.3а):
. Стационарные состояния водородоподобного атома описываются волновыми функциями (3.3а):
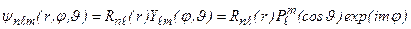 . (3.15)
. (3.15)
Функция 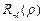 выражается через обобщенные полиномы Лягерра:
выражается через обобщенные полиномы Лягерра:
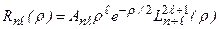 . (3.15а)
. (3.15а)

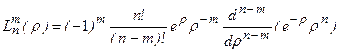 . При m=0 полиномы
. При m=0 полиномы  - полиномы Лягерра.
- полиномы Лягерра.
Состояние водородоподобного атома характеризуется набором чисел 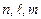 . Значение энергии каждого состояния (3.13) определяется только главным квантовым числом. Ситуация, при которой различным волновым функциям отвечает одно и то же значение энергии, характерна для вырожденных состояний. Для водородоподобного атома каждое значение энергии вырождено по магнитному квантовому числу и по орбитальному квантовому числу. Кратность вырождения уровней - это количество различных волновых функций, отвечающих одному и тому же значению энергии. Для водородоподобного атома кратность вырождения определяется суммой:
. Значение энергии каждого состояния (3.13) определяется только главным квантовым числом. Ситуация, при которой различным волновым функциям отвечает одно и то же значение энергии, характерна для вырожденных состояний. Для водородоподобного атома каждое значение энергии вырождено по магнитному квантовому числу и по орбитальному квантовому числу. Кратность вырождения уровней - это количество различных волновых функций, отвечающих одному и тому же значению энергии. Для водородоподобного атома кратность вырождения определяется суммой:
 . (3.16)
. (3.16)
Каждый уровень энергии водородоподобного атома является  – кратно вырожденным.
– кратно вырожденным.
Состояния электрона в атоме обозначают с помощью буквы, которая соответствует численному значению орбитального квантового числа, а также с помощью цифры, стоящей перед этой буквой и соответствующей значению главного квантового числа: 1s; 2s, 2p; 3s, 3p, 3d; 4s, 4p, 4d, 4f;... Диаграмма уровней энергии атома водорода - диаграмма Гротриана .
Состояние 1s –основное состояние. Остальные состояния возбужденные. Некоторые волновые функции для водородоподобного атома:
n = 1 – состояние 1s:
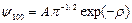 (3.17)
(3.17)
n = 2 – состояние 2s:
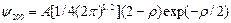
состояние 2p:
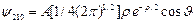
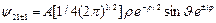 (3.17а)
(3.17а)
Постоянная 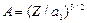 .
.
Переходы между различными состояниями возможны при выполнении правил отбора: 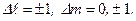
Квадрат модуля волновой функции (3.15) - плотность вероятности того, что электрон находится в элементе объема 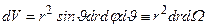 , где
, где 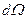 – элемент телесного угла:
– элемент телесного угла:
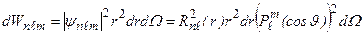 . (3.18)
. (3.18)
Распределения по углам и по радиусу - независимы. Вероятность углового распределения совпадает с вероятностью состояний ротатора. Распределение электронного заряда по радиусу:
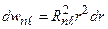 . (3.19)
. (3.19)
Условие нормировки  . Величина
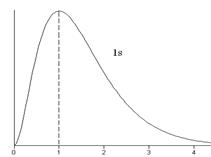
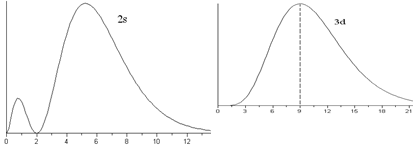
. Величина 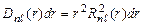 - вероятность того, что электрон находится на расстоянии от r до r + dr от ядра атома. Графики функции
- вероятность того, что электрон находится на расстоянии от r до r + dr от ядра атома. Графики функции 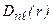 для некоторых состояний изображены на рис.3.3.
для некоторых состояний изображены на рис.3.3.
Функция  в состояниях с максимальным значением орбитального квантового числа
в состояниях с максимальным значением орбитального квантового числа  . Число
. Число 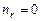 . Из (3.11):
. Из (3.11):  . Так что
. Так что  . Плотность вероятностей в этих состояниях:
. Плотность вероятностей в этих состояниях: 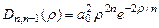 . Это «одногорбая» функция, имеет максимум при
. Это «одногорбая» функция, имеет максимум при 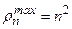 , т.е. на расстояниях
, т.е. на расстояниях 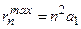 – радиусов боровских орбит. В состояниях 1s, 2p, 3d, 4f ,... наиболее вероятно найти электрон на расстояниях, равных боровским радиусам. . С возрастанием числа n ширина кривой
– радиусов боровских орбит. В состояниях 1s, 2p, 3d, 4f ,... наиболее вероятно найти электрон на расстояниях, равных боровским радиусам. . С возрастанием числа n ширина кривой 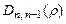 вблизи
вблизи 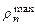 становится более узкой, при
становится более узкой, при 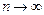 функция
функция 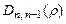 стремится к дельта–функции
стремится к дельта–функции 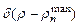 . В этом проявляется принцип соответствия. Для получения полной картины распределения электронной плотности в
. В этом проявляется принцип соответствия. Для получения полной картины распределения электронной плотности в
 |  | ||
пространстве необходимо учесть угловую зависимость по формуле (3.18).
Волновые функции (3.17)–(3.17в) описывают состояния с центрально–симметричным распределением заряда вокруг ядра, так что в этих состояниях электрический дипольный момент отсутствует. Из-за вырождения уровней энергии в атоме водорода существуют состояния с несимметричным распределением электронного заряда относительно плоскости z = 0. Например, суперпозиция волновых функций 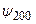 и
и 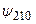 , отвечающих уровню энергии с n = 2:
, отвечающих уровню энергии с n = 2:
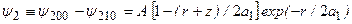 .
.
Эта волновая функция имеет узловую поверхность 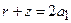 - параболоид вращения с осью z и фокус в начале координат. Распределение электронной плотности несимметрично относительно плоскости
- параболоид вращения с осью z и фокус в начале координат. Распределение электронной плотности несимметрично относительно плоскости 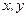 : среднее положение электрона вдоль оси z отлично от нуля:
: среднее положение электрона вдоль оси z отлично от нуля: 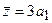 . В этом состоянии атом водорода обладает электрическим дипольным моментом.
. В этом состоянии атом водорода обладает электрическим дипольным моментом.
Лекция 17. Тонкая структура термов. Лэмбовский сдвиг
Учет спина электрона приводит к существенному изменению описания стационарных состояний атома. В этом случае каждое состояние описывается четверкой квантовых чисел: 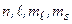 , где
, где  – магнитное спиновое квантовое число. Спин–орбитальное взаимодействие.Его происхождение: электрон находится в кулоновском поле с напряженностью
– магнитное спиновое квантовое число. Спин–орбитальное взаимодействие.Его происхождение: электрон находится в кулоновском поле с напряженностью  . В системе отсчета, жестко связанной с движущимся электроном, возникает магнитное поле (при
. В системе отсчета, жестко связанной с движущимся электроном, возникает магнитное поле (при 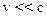 ):
):  . Поле
. Поле 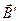 воздействует на спиновый магнитный момент электрона. Энергия этого взаимодействия:
воздействует на спиновый магнитный момент электрона. Энергия этого взаимодействия:
 .
.
Здесь  вектор орбитального момента импульса электрона,
вектор орбитального момента импульса электрона, 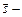 вектор спина. При точном расчете (Томас, Я.И. Френкель, 1926) энергия спин–орбитального взаимодействия в два раза меньше, чем
вектор спина. При точном расчете (Томас, Я.И. Френкель, 1926) энергия спин–орбитального взаимодействия в два раза меньше, чем  :
:

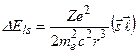 . (3.20)
. (3.20)
Для сравнения с опытом необходимо вычислить среднее значение энергии взаимодействия в n –ом состоянии:
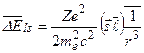 . (3.21)
. (3.21)
При спин–орбитальном взаимодействии длины векторов 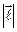 ,
, 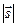 можно считать постоянными, так что определяющие их числа
можно считать постоянными, так что определяющие их числа 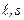 являются «хорошими» квантовыми числами. В этом случае используется векторная модель атома:векторы
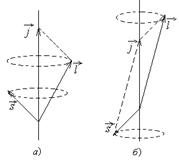
являются «хорошими» квантовыми числами. В этом случае используется векторная модель атома:векторы 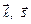 , складываясь, образуют вектор полного момента импульсаэлектрона в атоме (рис.3.4):
, складываясь, образуют вектор полного момента импульсаэлектрона в атоме (рис.3.4):
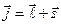 . (3.22)
. (3.22)
Рис.3.4 Для изолированной системы полный момент импульса сохраняется,
т.е. длина вектора 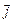 и его проекция на ось z имеют определенные значения. Длины векторов
и его проекция на ось z имеют определенные значения. Длины векторов 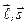 при этом сохраняются - они прецессируют вокруг направления вектора
при этом сохраняются - они прецессируют вокруг направления вектора  . Длина вектора
. Длина вектора 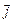 определяется квантовым числом j. Это квантовое число полного момента импульса, или внутреннее квантовое число (Зоммерфельд, 1920):
определяется квантовым числом j. Это квантовое число полного момента импульса, или внутреннее квантовое число (Зоммерфельд, 1920):
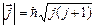 . (3.23)
. (3.23)
Проекции вектора 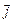 на ось z:
на ось z:
 , (3.24)
, (3.24)
где 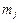 – магнитное квантовое число, связанное с полным моментом импульса. Это число при фиксированном значении числа j пробегает 2j+1 значений:
– магнитное квантовое число, связанное с полным моментом импульса. Это число при фиксированном значении числа j пробегает 2j+1 значений:
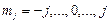 . (3.24a)
. (3.24a)
Возможные значения внутреннего квантового числа: проекция (3.22) на ось z: 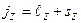 . Из
. Из 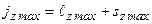 : число j имеет максимальное значение
: число j имеет максимальное значение  . Это соответствует «параллельному» расположению векторов
. Это соответствует «параллельному» расположению векторов  и
и 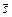 (рис.3.4а). Возможно также «антипараллельное» расположение векторов (рис.3.4б). При этом
(рис.3.4а). Возможно также «антипараллельное» расположение векторов (рис.3.4б). При этом 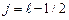 . Таким образом, в случае водородоподобного атома число j при фиксированном значении числа
. Таким образом, в случае водородоподобного атома число j при фиксированном значении числа 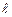 имеет два значения:
имеет два значения:
 . (3.24б)
. (3.24б)
Полное число значений, которое принимает внутреннее квантовое число - мультиплетность состояний(Каталан, 1923). Для атомов с одним электроном мультиплетность равна 2. Говорят, что состояния одноэлектронных атомов дублеты. С учетом спина каждое состояние водородоподобного атома и его уровни энергии расщепляются на два, кроме s–состояния, которое не расщепляется, а только несколько смещается. Расщепление уровней энергии, обусловленное спином электрона и релятивистскими эффектами - тонкая структура термов.
С учетом тонкой структуры рассмотренные ранее обозначения состояний водородоподобного атома необходимо уточнить (таблица 3). К прежним буквенным обозначениям состояний приписывают с правой стороны внизу соответствующее значение внутреннего квантового числа. С левой стороны вверху записывают мультиплетность состояния. Например, символ  означает:
означает: 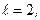
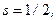
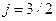 . Читают так: «дублет d три вторых».
. Читают так: «дублет d три вторых».
Таблица 3
j
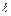
| 1/2 | 3/2 | 5/2 | 7/2 |
| ||||

| 
| |||
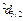
| 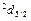
| |||

| 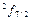
|
Возможность переходов между различными состояниями определяется правилами отбора не только для квантовых чисел 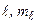 , но также для чисел
, но также для чисел  :
:
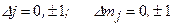 . (3.25)
. (3.25)
Правила (3.25) связаны с законом сохранения момента импульса в системе «атом + фотон».
Расчет величины расщепления энергетических уровней водородоподобного атома из-за спин–орбитального взаимодействия проводится по формуле (3.21):
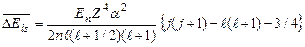 . (3.26a)
. (3.26a)
Использованы формулы: 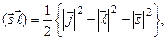
 . Величина
. Величина  – постоянная тонкой структуры,
– постоянная тонкой структуры,  – уровни энергии атома водорода,
– уровни энергии атома водорода,  – радиус первой боровской орбиты.
– радиус первой боровской орбиты.
Кроме указанного выше спин–орбитального взаимодействия, к расщеплению уровней энергии приводят также чисто релятивистские эффекты, так что 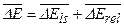 . Эта формула приводит к дополнительному слагаемому для спектрального терма:
. Эта формула приводит к дополнительному слагаемому для спектрального терма: 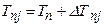 . Здесь
. Здесь 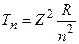 – бальмеровский терм. Величина
– бальмеровский терм. Величина 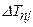 описывает тонкую структуру термов:
описывает тонкую структуру термов:
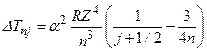 . (3.26)
. (3.26)
Такое же приближенное выражение получается в последовательной релятивистской теории Дирака(1928).
 При учете спин–орбитального взаимодействия состояния электрона в атоме описываются квантовыми числами
При учете спин–орбитального взаимодействия состояния электрона в атоме описываются квантовыми числами  . Так как энергия атома водорода согласно (3.26) не зависит от числа
. Так как энергия атома водорода согласно (3.26) не зависит от числа 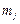 , то одному и тому же значению энергии отвечает
, то одному и тому же значению энергии отвечает 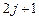 состояний: состояния атома водорода являются вырожденными по квантовому числу
состояний: состояния атома водорода являются вырожденными по квантовому числу 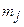 с кратностью вырождения
с кратностью вырождения 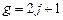 . Это число - статистический вес уровня энергии nj.
. Это число - статистический вес уровня энергии nj.
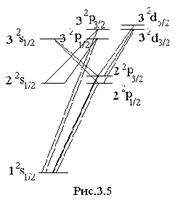
 Без учета поправки
Без учета поправки 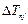 состояния водородоподобного атома вырождены. Учет этой поправки частично снимает вырождение: одному и тому же значению главного квантового числа, но разным значениям числа j,отвечают разные термы, т.е. разные значения энергии. Таким образом, диаграмма уровней энергии атома водорода (рис.3.2) требует дальнейших уточнений. Согласно (3.26), состояния с одним и тем же числом n и одинаковыми значениями числа j имеют одно и то же значение энергии. Например, при n = 2 из трех состояний
состояния водородоподобного атома вырождены. Учет этой поправки частично снимает вырождение: одному и тому же значению главного квантового числа, но разным значениям числа j,отвечают разные термы, т.е. разные значения энергии. Таким образом, диаграмма уровней энергии атома водорода (рис.3.2) требует дальнейших уточнений. Согласно (3.26), состояния с одним и тем же числом n и одинаковыми значениями числа j имеют одно и то же значение энергии. Например, при n = 2 из трех состояний 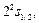
 два первых состояния имеют одинаковое значение энергии. Таким образом, при n = 2 имеется не три, а два различных уровня энергии. При n = 3 не пять, а три различных уровня и т. д. (рис.3.5). Поправка тонкой структуры
два первых состояния имеют одинаковое значение энергии. Таким образом, при n = 2 имеется не три, а два различных уровня энергии. При n = 3 не пять, а три различных уровня и т. д. (рис.3.5). Поправка тонкой структуры 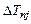 мала, так как мала величина
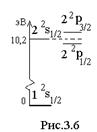
мала, так как мала величина  . Тонкая структура термов наиболее существенна при значении n = 2. Тонкая структура термов приводит к тонкой структуре спектральных линий. Спектральные линии серии Лаймана являются дублетами (рис.3.5). Линия
. Тонкая структура термов наиболее существенна при значении n = 2. Тонкая структура термов приводит к тонкой структуре спектральных линий. Спектральные линии серии Лаймана являются дублетами (рис.3.5). Линия 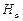 бальмеровской серии имеет более сложную структуру. Она состоит из пяти компонентов. Структура этой линии атома водорода
бальмеровской серии имеет более сложную структуру. Она состоит из пяти компонентов. Структура этой линии атома водорода 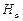 тщательно изучалась экспериментально. При этом получались противоречивые результаты. В 1947 г. Лэмби Ризерфордвыполнили решающий эксперимент. Они показали, что в отличие от выводов из формулы Дирака (3.26), состояния
тщательно изучалась экспериментально. При этом получались противоречивые результаты. В 1947 г. Лэмби Ризерфордвыполнили решающий эксперимент. Они показали, что в отличие от выводов из формулы Дирака (3.26), состояния 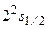 и
и 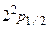 отвечают разным значениям энергии (рис.3.6). Смещение уровня
отвечают разным значениям энергии (рис.3.6). Смещение уровня 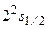 относительно уровня
относительно уровня 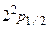 - лэмбовский сдвиг.Разности между подуровнями
- лэмбовский сдвиг.Разности между подуровнями 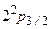 и
и 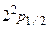 соответствует частота около
соответствует частота около 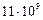 Гц = 11 ГГц (энергия – около
Гц = 11 ГГц (энергия – около 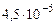 эВ, длина волны – 2,74 см). Это – радиочастотный диапазон. Лэмбовский сдвиг соответствует частоте 1 ГГц (волновое число 0,0359 см
эВ, длина волны – 2,74 см). Это – радиочастотный диапазон. Лэмбовский сдвиг соответствует частоте 1 ГГц (волновое число 0,0359 см  ).
).
 Уровень
Уровень 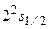 (энергия 10,2 эВ) метастабильный (время жизни 0,122 с): прямой переход с этого уровня в основное состояние запрещен правилом отбора
(энергия 10,2 эВ) метастабильный (время жизни 0,122 с): прямой переход с этого уровня в основное состояние запрещен правилом отбора  . Другой возможный переход на уровень
. Другой возможный переход на уровень 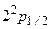 имеет ничтожную вероятность. Возбужденное состояние
имеет ничтожную вероятность. Возбужденное состояние 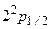 является короткоживущим: за время
является короткоживущим: за время 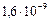 с из него совершается переход в основное состояние с излучением волны
с из него совершается переход в основное состояние с излучением волны 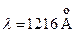 . Так же быстро происходит переход из состояния
. Так же быстро происходит переход из состояния 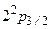 .
.
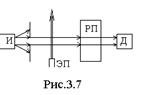
Упрощенная схема опыта Лэмба и Ризерфорда (рис.3.7). Пучок атомарного водорода в основном состоянии создавался источником – И. Этот пучок бомбардировался электронами, вылетающими из электронной пушки – ЭПс энергией 10,8 эВ. При этом примерно один из  атомов водорода переходил в метастабильное состояние
атомов водорода переходил в метастабильное состояние 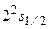 . Специально разработанный детектор – Д регистрировал такие возбужденные атомы. Если на пути пучка возбужденных атомов поместить радиочастотное поле – РП, то оно будет индуцировать переходы атомов в одно из 2p–состояний. Такие переходы носят резонансный характер: они совершаются при совпадении частоты радиочастотного поля с частотой перехода
. Специально разработанный детектор – Д регистрировал такие возбужденные атомы. Если на пути пучка возбужденных атомов поместить радиочастотное поле – РП, то оно будет индуцировать переходы атомов в одно из 2p–состояний. Такие переходы носят резонансный характер: они совершаются при совпадении частоты радиочастотного поля с частотой перехода 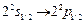 (1 ГГц) или с частотой перехода
(1 ГГц) или с частотой перехода 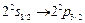 (10 ГГц). В результате таких переходов резко уменьшалось число возбужденных атомов, что регистрировалось детектором.
(10 ГГц). В результате таких переходов резко уменьшалось число возбужденных атомов, что регистрировалось детектором.
Важное значение опыта Лэмба -Ризерфорда в том, что он показал ограниченность теории Дирака и стимулировал развитие релятивистской квантовой теории взаимодействия электрона с электромагнитным полем. В то время теория Дирака считалась самой последовательной теорией, поскольку она была релятивистской и автоматически учитывала спин электрона. Поиски объяснения лэмбовского сдвига привели к коренному пересмотру основ квантовой теории и возникновению квантовой электродинамикии квантовой теории поля. Оказалось, что вакуум, в котором находятся электроны и ядро атома, нельзя рассматривать как пустоту, которая ничего не содержит. Напротив, вакуум обладает определенными физическими свойствами. В частности, существуют нулевые колебания вакуума. Эти колебания вызывают «дрожание» электрона в атоме, так что его потенциальная энергия изменяется. Это и приводит к лэмбовскому сдвигу.
Дата добавления: 2015-12-16; просмотров: 2735;
