Электронный парамагнитный резонанс.
Эффект Зеемана - расщепление уровней энергии и спектральных линий излучающего атома в магнитном поле. По Лоренцу: в магнитном поле с индукцией В должен наблюдаться лоренцевский триплетс частотами:
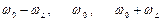 . (3.55)
. (3.55)
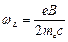 – ларморовская частота прецессии (Лармор, 1897). Таков же результат квантовой теории (Дебай, Зоммерфельд, 1916): проекция магнитного момента орбитального движения электронов в атоме, на выделенное направление -
– ларморовская частота прецессии (Лармор, 1897). Таков же результат квантовой теории (Дебай, Зоммерфельд, 1916): проекция магнитного момента орбитального движения электронов в атоме, на выделенное направление - 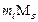 (
( 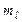 магнитное квантовое число,
магнитное квантовое число, 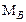 – магнетон Бора). Для атома, помещенного в магнитное поле, выделенным является направление магнитного поля. В этом поле дополнительная энергия атома:
– магнетон Бора). Для атома, помещенного в магнитное поле, выделенным является направление магнитного поля. В этом поле дополнительная энергия атома:
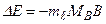 . (3.55a)
. (3.55a)
Каждый уровень энергии расщепляется на 2 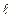 +1 подуровней. Уровни энергии атома в магнитном поле:
+1 подуровней. Уровни энергии атома в магнитном поле:
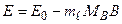 .
.
Частота линии излучения (или поглощения):
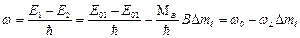 . (3.55б)
. (3.55б)
 Величина
Величина 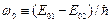 - частота линии излучения атома в отсутствие магнитного поля. По правилу отбора
- частота линии излучения атома в отсутствие магнитного поля. По правилу отбора 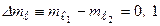 приходим к лоренцевскому триплету.
приходим к лоренцевскому триплету.
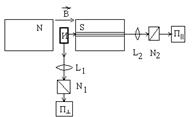
Для наблюдения эффекта Зеемана (рис.3.24) между полюсами сильного электромагнита, создающего однородное магнитное поле, помещался источник линейчатого спектра И. Наблюдения проводились поперек и вдоль магнитного поля. Излучаемый свет фокусировался линзой 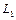 (или
(или 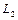 ). Характер поляризации света определялся с помощью анализатора
). Характер поляризации света определялся с помощью анализатора 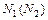 . Далее свет попадал
. Далее свет попадал
Рис.3.24 в спектральный прибор 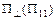 большой разрешающей силы.
большой разрешающей силы.
При наблюдении поперек магнитного поля для некоторых простых синглетных линий, например, ртути, кадмия и др. обнаруживается лоренцевский триплет (3.55). При продольном наблюдении возникает дублет, так как линия с частотой 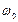 отсутствует.
отсутствует.
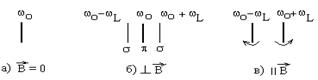
Рис.3.25
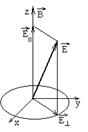 Наблюдаемые линии излучения в продольном и поперечном эффекте имеют разную поляризацию (рис.3.25). Без магнитного поля (рис.3.25а) излучение не поляризовано. При поперечном наблюдении (рис.3.25б) крайние компоненты поляризованы так, что колебания в них перпендикулярны направлению магнитного поля (
Наблюдаемые линии излучения в продольном и поперечном эффекте имеют разную поляризацию (рис.3.25). Без магнитного поля (рис.3.25а) излучение не поляризовано. При поперечном наблюдении (рис.3.25б) крайние компоненты поляризованы так, что колебания в них перпендикулярны направлению магнитного поля ( 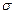 –компоненты), а несмещенная линия соответствует колебаниям вдоль магнитного поля (
–компоненты), а несмещенная линия соответствует колебаниям вдоль магнитного поля ( 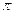 –компонента). При продольном наблюдении (рис.3.25в) излучаемые линии имеют круговую поляризацию. Это легко понять с помощью рис.3.26, учитывая, что излучение поперечная волна, так
–компонента). При продольном наблюдении (рис.3.25в) излучаемые линии имеют круговую поляризацию. Это легко понять с помощью рис.3.26, учитывая, что излучение поперечная волна, так
Рис.3.26 что волновой вектор 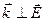 , где
, где  – вектор напряженности электрического поля
– вектор напряженности электрического поля
излучения.
Измеряя на опыте величину зеемановского расщепления и величину индукции магнитного поля, можно вычислить отношение 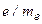 . Найденное значение согласуется с измеренными значениями этого отношения другими методами.
. Найденное значение согласуется с измеренными значениями этого отношения другими методами.
На опыте чаще наблюдается не лоренцевское расщепление, а более сложная картина - сложный, или аномальный эффект Зеемана. Его не удавалось объяснить до открытия спина электрона.
Учет тонкой структуры термов объясняет мультиплетное расщепление спектральных линий. Магнитное поле также приводит к их расщеплению, определяемому ларморовской частотой. Характер расщепления спектральных линий зависит от величины напряженности магнитного поля. Различают случаи «слабого»и«сильного» магнитного поля. Если расщепление, вызываемое магнитным полем, мало по сравнению с естественным мультиплетным расщеплением 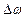 (
( 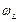 <<
<< 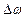 ), то поле «слабое»: В противном случае магнитное поле «сильное». Эти понятия имеют относительный смысл. Например, для D–линии натрия магнитное поле слабое, если В <<
), то поле «слабое»: В противном случае магнитное поле «сильное». Эти понятия имеют относительный смысл. Например, для D–линии натрия магнитное поле слабое, если В <<  Гс; для первой линии лаймановской серии атома водорода слабыми являются поля В <<
Гс; для первой линии лаймановской серии атома водорода слабыми являются поля В << 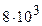 Гс. Магнитное поле, в котором
Гс. Магнитное поле, в котором 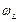 =
= 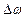 , называют критическим.
, называют критическим.
Случай слабого магнитного поля. Спин–орбитальное взаимодействие, приводящее к тонкой структуре, является более сильным, чем взаимодействие по отдельности магнитного спинового и магнитного орбитального моментов с внешним магнитным полем. Предполагается, что осуществляется нормальный тип связи атомных моментов. Полный момент импульса атома 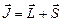 , полный магнитный момент
, полный магнитный момент  , где
, где 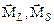 – магнитные моменты, связанные с полным орбитальным и спиновым движениями, соответственно. Во внешнем магнитном поле атом приобретает дополнительную энергию
– магнитные моменты, связанные с полным орбитальным и спиновым движениями, соответственно. Во внешнем магнитном поле атом приобретает дополнительную энергию
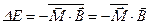 , (3.56)
, (3.56)
черта сверху - среднее значение по времени. Если бы полный магнитный момент атома  был параллелен полному механическому моменту
был параллелен полному механическому моменту 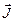 , то из (3.56), как и из (3.55а, б), следовало бы, что происходит лоренцевское расщепление. Однако это не так. В этом что причина аномального Зееман–эффекта. Магнитные орбитальный и спиновый моменты связаны с соответствующими механическими моментами соотношениями (рис.3.27):
, то из (3.56), как и из (3.55а, б), следовало бы, что происходит лоренцевское расщепление. Однако это не так. В этом что причина аномального Зееман–эффекта. Магнитные орбитальный и спиновый моменты связаны с соответствующими механическими моментами соотношениями (рис.3.27):
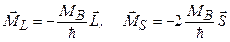 . (3.57)
. (3.57)
 Векторы
Векторы 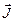 и
и  не параллельны друг другу. При спин–орбитальном взаимодействия сохраняются длины
не параллельны друг другу. При спин–орбитальном взаимодействия сохраняются длины 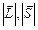 векторов
векторов 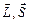 , а также их проекции на направление вектора
, а также их проекции на направление вектора 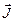 : векторы
: векторы 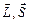 прецессируют вокруг момента
прецессируют вокруг момента 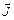 . Вместе с ними прецессируют векторы
. Вместе с ними прецессируют векторы 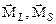 и вектор магнитного момента
и вектор магнитного момента  . Вектор
. Вектор 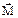 имеет составляющую
имеет составляющую 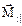 вдоль вектора
вдоль вектора 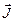 и составляющую
и составляющую 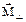 , перпендикулярную ему:
, перпендикулярную ему:
Рис.3.27  =
= 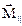 +
+ 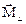 . (3.57а)
. (3.57а)
Вследствие прецессии вектора  вокруг вектора
вокруг вектора 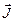 составляющая
составляющая 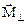 быстро вращается - ее среднее значение по времени равно нулю. Составляющая
быстро вращается - ее среднее значение по времени равно нулю. Составляющая 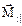 не изменяется:
не изменяется:
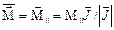 . (3.57б)
. (3.57б)
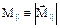 – величина (модуль) вектора
– величина (модуль) вектора 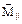 . Дополнительная энергия атома (3.55) в магнитном поле:
. Дополнительная энергия атома (3.55) в магнитном поле: 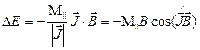 . (3.58)
. (3.58)
Вычислим 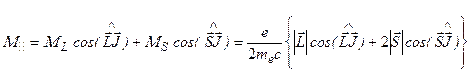 . Из рис.3.27:
. Из рис.3.27:
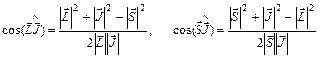 .
.
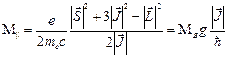 . (3.59)
. (3.59)
Постоянная:
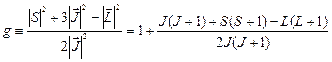 (3.59a)
(3.59a)
фактор,или множитель Ланде(1923). Если магнитное поле 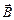 направлено вдоль оси z, то из (3.58), (3.59):
направлено вдоль оси z, то из (3.58), (3.59):
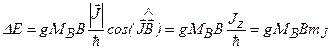 . (3.60)
. (3.60)
В слабом магнитном поле каждый уровень энергии атома расщепляется на 2J +1 подуровней. При заданных квантовых числах фактор Ланде для разных термов заранее можно рассчитать (табл. 9):
Таблица 9
| Состояния | 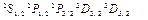
| 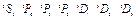
|
| g | 2 2/3 4/3 4/5 6/5 | 2 - 3/2 3/2 1/2 7/6 4/3 |
 Расщепление в слабом магнитном поле спектральной линии при переходе между состояниями «1» и «2»:
Расщепление в слабом магнитном поле спектральной линии при переходе между состояниями «1» и «2»:
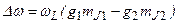 , (3.61)
, (3.61)
переходы определяются правилами отбора: 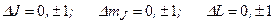 .
.
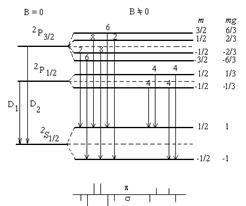
Пример: расщепление D–линии (дублета) атома натрия (рис.3.28). Линия 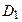 расщепляется на 4 компоненты с расщеплением частоты (в единицах
расщепляется на 4 компоненты с расщеплением частоты (в единицах 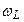 ):
): 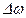 = 4/3, 2/3, –2/3, –4/3. Линия
= 4/3, 2/3, –2/3, –4/3. Линия 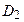 расщепляется на 6 компонент с расщеплением
расщепляется на 6 компонент с расщеплением 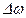 = 5/3, 3/3, 1/3, –1/3, –3/3, –5/3. Таким образом, в магнитном поле D–дублет
= 5/3, 3/3, 1/3, –1/3, –3/3, –5/3. Таким образом, в магнитном поле D–дублет
Рис.3.28 натрия расщепляется на 10 линий, при этом линии 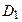 ,
, 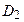
 отсутствуют. Это наблюдается на опыте.
отсутствуют. Это наблюдается на опыте.
В случае сильного магнитного поля взаимодействие орбитального и спинового магнитных моментов по отдельности с магнитным полем превосходит их взаимодействие между собой. Следовательно, дополнительная энергия атома:
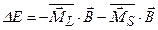 . (3.62)
. (3.62)
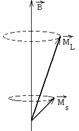
Модули векторов 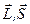 постоянны. Постоянны также их проекции на направление магнитного поля (ось z). Векторы
постоянны. Постоянны также их проекции на направление магнитного поля (ось z). Векторы 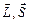 , а также векторы
, а также векторы 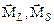 прецессируют вокруг направления магнитного поля (рис.3.29). Таким образом, дополнительная Рис.3.29
прецессируют вокруг направления магнитного поля (рис.3.29). Таким образом, дополнительная Рис.3.29
энергия атома:
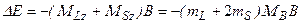 . (3.62a)
. (3.62a)
В сильном магнитном поле наблюдается (2L+1)(2S+1) подуровней. Расщепление спектральной линии при переходах между состояниями «1» и «2»:
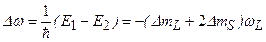 . (3.63)
. (3.63)
По правилам отбора: 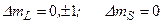 . Поэтому:
. Поэтому: 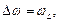 0,
0, 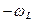 . В сильном магнитном поле наблюдается простой лоренцевский триплет. Это эффект Пашена-Бака(1912), илимагнитооптическое превращение.
. В сильном магнитном поле наблюдается простой лоренцевский триплет. Это эффект Пашена-Бака(1912), илимагнитооптическое превращение.
Дата добавления: 2015-12-16; просмотров: 1104;
