Лекция 23. Электронный парамагнитный резонанс

Зееман-эффект связан с переходами между подуровнями расщепленных в магнитном поле разных энергетических уровней. Такие переходы соответствуют оптическому диапазону частот. Наряду с этим возможны переходы между соседними подуровнями расщепившегося в магнитном поле уровня энергии согласно правилам отбора:

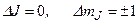. (3.64)

Таким переходам соответствуют частоты:

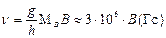Гц. (3.65)

При В 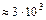Гс частота 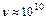Гц, а длина волны 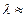3 см. Это – микроволновый диапазон частот (диапазон СВЧ). Вероятность дипольных переходов, которая пропорциональна 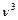, в СВЧ диапазоне ничтожно мала по сравнению с вероятностью в оптическом диапазоне. Кроме того, для атомов с одним валентным электроном переходы запрещены правилом отбора 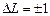. Однако вероятность переходов становится значительной при наложении дополнительного внешнего переменногомагнитного поля, т.е. когда переходы становятся вынужденными. Если частота переменного магнитного поля равна частоте перехода (3.65), то происходит поглощение энергии этого поля или вынужденное излучение. При этом скачком изменяется ориентация магнитного момента атома, т.е. его проекция на выделенное направление.

Излучение или поглощение электромагнитных волн при изменении ориентации магнитных дипольных моментов атомов в магнитном поле называют явлением магнитного резонанса.

Последовательное описание магнитного резонанса довольно сложно. Качественную картину этого явления можно понять на основе простой классической модели. Если частица обладает магнитным моментом 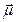, то во внешнем постоянном магнитном поле 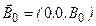на нее действует вращающий момент 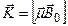. Магнитный 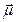и механический 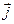моменты частицы (например, электрона в атоме) связаны:

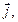(3.66)

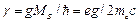– гиромагнитное отношение. Уравнение движения:

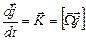. (3.67а)

Это уравнение волчка: механический и магнитный моменты совершают прецессию вокруг 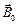. Угловая скорость (частота) прецессии:

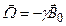. (3.68)

В магнитном поле, направленном вдоль оси z, частица приобретает дополнительную энергию:

.

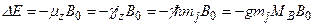Частота перехода между соседними подуровнями энергии совпадает с частотой прецессии:

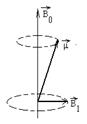
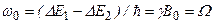. (3.68а)

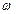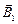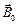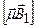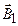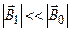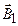Если добавить изменяющееся с частотой магнитное поле , перпендикулярное стационарному полю (рис. 3.31), то на частицу будет действовать дополнительный переменный вращающий момент . Когда частота прецессии и частота изменения поля сильно отличаются друг от друга, то при поле приводит только к периодическому изменению угла наклона магнитного Рис.3.31 момента к оси z - в среднем этот угол не меняется. Если частота изменения поля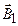

совпадает с частотой прецессии (3.68), то магнитный момент оказывается как бы в статических условиях и дополнительный вращающий момент стремится «опрокинуть» магнитный момент. Поскольку магнитный момент является квантовым вектором, то его проекция на направление статического магнитного поля может только скачком измениться на противоположное значение. В этом состоит явление магнитного резонанса.

Еслимагнитный и механический моменты атома обусловлены его электронами, то магнитный резонанс называют электронным парамагнитным резонансом(ЭПР).Когда моменты определяются ядром атома, то магнитный резонанс называют ядерным магнитным резонансом(ЯМР),который первым наблюдался в опытах с молекулярными пучками (Раби, 1938). Существуют также ферромагнитныйиантиферромагнитный резонансы, связанные с изменениемориентации электронных магнитных моментов в ферромагнетиках и антиферромагнетиках.

Электронным парамагнетизмом обладают: все атомы и молекулы с нечетным числом электронов (неспаренные, нескомпенсированные электроны) на внешних электронных оболочках, поскольку в этом случае полный спин системы не равен нулю (свободные атомы натрия, газообразная окись азота и т.д.); атомы и ионы с незаполненной внутренней электронной оболочкой (редкоземельные элементы, актиниды и др.) и т.п. ЭПР представляет собой совокупность явлений, связанных с квантовыми переходами, происходящими между энергетическими уровнями макроскопических систем под влиянием переменного магнитного поля резонансной частоты

В эксперименте явление ЭПР впервые наблюдал Е.К. Завойский (1944). ЭПР служит мощным средством изучения свойств парамагнитных веществ в макроскопических количествах. Макроскопической магнитной характеристикой вещества является вектор намагничивания 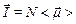, где N – число частиц в единице объема вещества, – средний магнитный момент частиц. Систему моментов всех парамагнитных частиц данного вещества называют спин–системой.Остальные степени свободы парамагнетика – окружение магнитных моментов называют «решеткой». В связи с этим рассматривают два типа взаимодействий: взаимодействие магнитных моментов между собой (спин–спиновое взаимодействие) и взаимодействие магнитных моментов со своим окружением (спин–решеточное взаимодействие). В изолированной спин–системе стационарного поглощения энергии переменного поля не может происходить. В самом деле, до включения переменного магнитного поля число частиц в основном состоянии 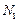больше их числа 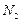в возбужденном состоянии. При поглощении энергии число частиц 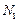уменьшается, а число 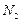увеличивается. Это будет происходить, пока числа 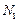и 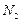не сравняются. Тогда достигается насыщение, и дальнейшее поглощение энергии прекращается. С учетом взаимодействия спин–системы с решеткой стационарное поглощение энергии становится возможным. Решетка служит в качестве стока энергии и в этом процессе она нагревается. Изменение вектора намагничивания описывается уравнением Блоха(1946):

, (3.69)

где 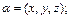величина 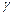– гиромагнитное отношение; 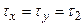– время спин–спиновой (или поперечной) релаксации; 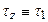– время спин–решеточной (или продольной) релаксации; – равновесное значение вектора намагничивания в постоянном магнитном поле 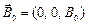. Значения величин 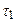и 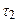зависят от особенностей взаимодействия каждой частицы с

Рис.3.32 окружающими ее частицами. Определение этих времен релаксации - основная

экспериментальная задача метода магнитного резонанса. В уравнениях (3.69) первый член записан по аналогии с уравнением движения одиночного магнитного момента (3.67). Вторые члены обусловлены спин–спиновым и спин–решеточным взаимодействиями, которые определяют достижение системой равновесного состояния. Поглощаемая парамагнитным веществом мощность излучения 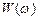вычисляется с помощью уравнений (3.69):

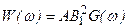, (3.70)

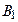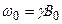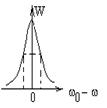
где А – некоторый множитель, – амплитуда переменного магнитного поля; – частота прецессии. Форма кривой поглощения определяется функцией:

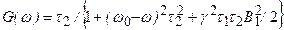. (3.70а)

Кривая поглощения (рис.3.32) имеет лоренцевскую форму. Ее максимум при резонансе: 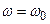. Ширина линии поглощения: 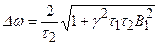. (3.70б)

В достаточно слабом высокочастотном магнитном поле ширина кривой поглощения определяется временем спин–спиновой релаксации. С увеличением этого поля линия поглощения уширяется. По ширине кривой поглощения определяют времена релаксации, которые связаны со свойствами вещества.

Метод ЭПР обладает высокой чувствительностью. Он позволяет измерять времена релаксации, ядерные магнитные моменты, проводить количественный анализ любых парамагнитных веществ вплоть до 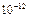г вещества, определять структуру химических соединений, электронные конфигурации, измерять слабые напряженности магнитного поля от 2 до 100 Э и т.д.