Вынужденные колебания. Резонанс
В некоторых случаях колебания могут происходить под действием внешних сил.
Вынужденные колебания возникают в системе при участии внешней силы, изменяющейся по периодическому закону.
Рассмотрим случай, когда на тело помимо упругой силы F и силы трения Fтрдействует еще и вынуждающая гармоническая сила fb= F0·соs(ωв ·t), где F0— амплитуда силы; ωв — круговая частота ее колебаний.
Запишем дифференциальное уравнение движения, вытекающее из второго закона Ньютона:
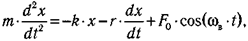
или
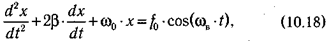
где
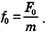
Можно показать, что для больших значениях t решение этого уравнения определяется формулой:
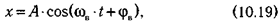
где φв — разность фаз между силой Fв и смещением х.
Таким образом, установившиеся вынужденные колебания, происходящие под воздействием гармонически изменяющейся силы, являются тоже гармоническими. Их частота равна частоте вынуждающей силы.
Амплитуда А установившихся вынужденных колебаний зависит от собственной частоты колебаний, массы материальной точки, амплитуды и частоты вынуждающей силы и коэффициента затухания:
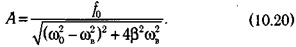
Вибрация
Одним из проявлений вынужденных колебаний является вибрация. Вибрация используется при массаже. При ручном массаже массируемые ткани приводятся в колебательное движение при помощи рук массажиста. При аппаратном массаже используются вибрационные аппараты, которые подразделяются на аппараты для общей вибрации, вызывающие сотрясение всего тела (вибрационные «стул», «кровать», «платформа» и др.) и аппараты местного вибрационного воздействия.
Резонанс
Если ω0 и β для системы заданы, то амплитуда вынужденных колебаний имеет максимальное значение при некоторой определенной частоте вынуждающей силы, называемой резонансной. Само явление — достижение максимальной амплитуды вынужденных колебаний при определенном значении частоты вынуждающей силы называется резонансом.
Резонансную круговую частоту можно найти, если определить условие минимума знаменателя в (10.20):

При этой частоте имеет место максимум амплитуды вынужденных колебаний, определяемый формулой:
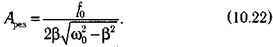
Дата добавления: 2015-11-28; просмотров: 998;
