Вынужденные динамические погрешности
Вынужденные динамические погрешности возникают в результате воздействия помех и наводок, как внешних по отношению к измерительной системе, так и внутренних, генерируемых в ее звеньях или в каналах связи.
По характеру воздействия на измерительную систему можно выделить два принципиально различных типа шумов.
1). Аддитивные шумы – это шумы, которые складываются с полезным сигналом в некоторых точках структуры измерительной системы.
2). Мультипликативные шумы – это шумы, действие которых приводит к тому, что коэффициенты дифференциального уравнения измерительной системы становятся переменными и содержат в своем составе случайную составляющую (шумят).
Анализ мультипликативных шумов представляет собой очень сложную задачу. Хорошо то, что на практике чаще приходится встречаться именно с аддитивными шумами, анализ воздействия которых значительно проще.

 Пусть в определенных точках структуры измерительной системы действуют аддитивные помехи
Пусть в определенных точках структуры измерительной системы действуют аддитивные помехи  в форме случайных стационарных процессов с энергетическими спектрами
в форме случайных стационарных процессов с энергетическими спектрами 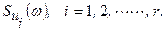
Перестроим структуру системы таким образом, чтобы помеха 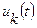 стала входным сигналом, полагая все остальные помехи и измерительный сигнал равными нулю. Проделывая эту процедуру для каждой помехи, можно получить все преобразованные структуры и определить их передаточные функции
стала входным сигналом, полагая все остальные помехи и измерительный сигнал равными нулю. Проделывая эту процедуру для каждой помехи, можно получить все преобразованные структуры и определить их передаточные функции 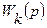 , которые являются передаточными функциями помех.
, которые являются передаточными функциями помех.
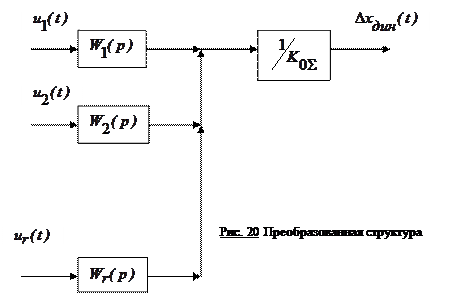
Объединим выходы всех этих систем (рис. 20) и введем фиктивное статическое звено с чувствительностью, обратной чувствительности исходной измерительной системы. На выходе этого звена образуется сигнал, являющийся вынужденной динамической погрешностью, определяемой действием рассмотренных аддитивных шумов.
Из преобразованной по шумам структуры видно, что преобразование Лапласа для вынужденной динамической погрешности 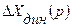 определяется теперь передаточными функциями помех и преобразованиями Лапласа
определяется теперь передаточными функциями помех и преобразованиями Лапласа 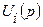 для действующих аддитивных помех
для действующих аддитивных помех  :
:
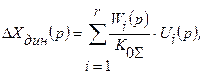 ,
,
поэтому энергетический спектр вынужденной динамической погрешности должен составлять:
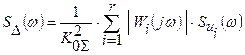 ,
,
а дисперсия вынужденной динамической погрешности равна
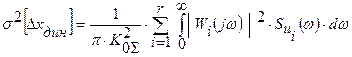 .
.
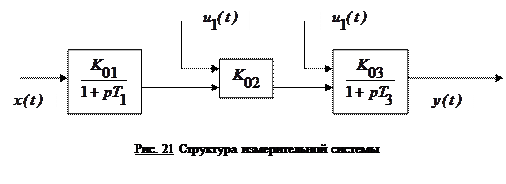 |
Пример. Измерительная система в укрупненном виде имеет структуру, представленную на рис.21.
На рисунке приняты следующие обозначения:
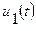 - помеха типа белого шума со спектральной плотностью
- помеха типа белого шума со спектральной плотностью 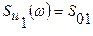 , постоянной в полосе частот, большей частотного диапазона системы,
, постоянной в полосе частот, большей частотного диапазона системы,
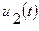 - синусоидальная помеха на частоте
- синусоидальная помеха на частоте 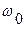 , то есть помеха со спектральной плотностью
, то есть помеха со спектральной плотностью 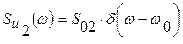 .
.
Перестроим структуру измерительной системы по помехам (рис. 22)
 |
Дисперсия вынужденной погрешности
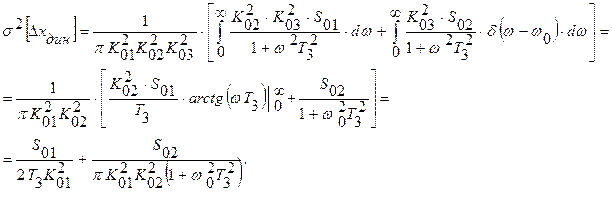
Здесь интересно отметить, что вынужденная динамическая погрешность уменьшается с увеличением постоянной времени T3, то есть с уменьшением частотного диапазона системы. Однако при этом увеличивается собственна динамическая погрешность. Поэтому задача определения необходимого частотного диапазона требует одновременного учета обеих составляющих динамической погрешности.
Дата добавления: 2015-11-28; просмотров: 1005;
