Собственные динамические погрешности
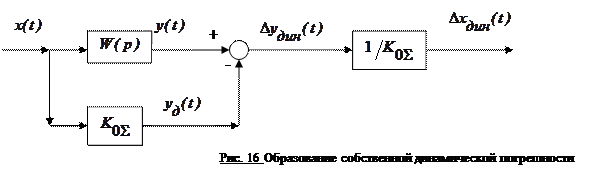
Общий механизм образования собственной динамической погрешности можно иллюстрировать следующей схемой, приведенной на рис. 16.
На вход измерительной системы с передаточной функцией  поступает входной сигнал
поступает входной сигнал 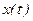 . На выходе имеет место сигнал
. На выходе имеет место сигнал  , равный
, равный
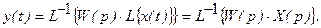
Если бы измерительная система не вносила динамических искажений, она должна была бы обладать передаточной функцией, постоянной в своем частотном диапазоне

Поэтому сигнал на выходе измерительной системы имел бы вид:
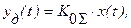
что формально можно записать в виде:

Динамическая погрешность – это разность сигналов  и
и  :
:
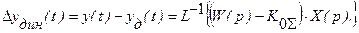
Для приведения ко входу ее теперь нужно разделить на чувствительность системы ко входному сигналу:

Изображенную выше структуру можно теперь представить в виде, представленном на рис. 17.
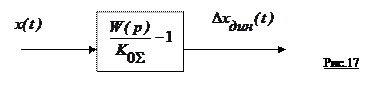 Выражение
Выражение
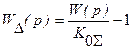
называется передаточной функцией ошибки.
Если 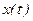 является квазидетерминированным сигналом, то он содержит в себе некоторые случайные параметры
является квазидетерминированным сигналом, то он содержит в себе некоторые случайные параметры 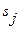 , которые и делают этот сигнал почти случайным
, которые и делают этот сигнал почти случайным 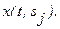 Поэтому и отображение
Поэтому и отображение 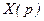 сигнала содержит в себе эти параметры. В этих условиях и динамическая погрешность
сигнала содержит в себе эти параметры. В этих условиях и динамическая погрешность 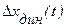 является квазидетерминированной функцией
является квазидетерминированной функцией  , случайность которой характеризуется теми же случайными параметрами
, случайность которой характеризуется теми же случайными параметрами 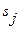 . Вероятностные характеристики динамической погрешности определяются при этом уже известными методами. Если для каждого
. Вероятностные характеристики динамической погрешности определяются при этом уже известными методами. Если для каждого 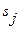 известны математическое ожидание
известны математическое ожидание 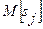 и дисперсия
и дисперсия 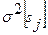 , причем
, причем  , то вероятностные характеристики динамической погрешности составляют:
, то вероятностные характеристики динамической погрешности составляют:
математическое ожидание  ,
,
дисперсия 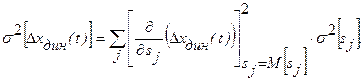
Если 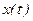 является реализацией случайного стационарного эргодического процесса с энергетическим спектром
является реализацией случайного стационарного эргодического процесса с энергетическим спектром  , то спектральная плотность динамической погрешности оказывается равной произведению спектра
, то спектральная плотность динамической погрешности оказывается равной произведению спектра  и квадрата модуля АФЧХ ошибки:
и квадрата модуля АФЧХ ошибки:

и дисперсия динамической погрешности определяется теперь интегралом спектральной плотности погрешности:
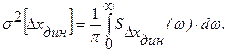
Рассмотрим несколько типовых примеров определения динамических погрешностей.
1. Измерение постоянных величин в неустановившемся режиме при ограниченном времени измерения.

 Этот случай характерен для использования контрольных автоматов циклического действия, когда контролируемые изделия одно за другим, с периодом времени
Этот случай характерен для использования контрольных автоматов циклического действия, когда контролируемые изделия одно за другим, с периодом времени 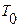 , поступают на позицию измерения и затем уходят с нее (рис. 17).
, поступают на позицию измерения и затем уходят с нее (рис. 17).
В этом случае можно считать, что измеряемая величина в некоторый момент времени принимает значение 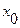 , остается равной
, остается равной 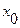 в течение времени
в течение времени 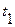 и затем вновь уменьшается до некоторого исходного уровня. Через время
и затем вновь уменьшается до некоторого исходного уровня. Через время 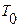 процесс повторяется, причем измеряемая величина принимает новое значение
процесс повторяется, причем измеряемая величина принимает новое значение 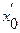 . Выходной сигнал измерительной системы изменяется в соответствии с переходной функцией
. Выходной сигнал измерительной системы изменяется в соответствии с переходной функцией  . Для повышения производительности контрольного автомата время нахождения изделия на позиции измерения может быть и меньше продолжительности переходного процесса.
. Для повышения производительности контрольного автомата время нахождения изделия на позиции измерения может быть и меньше продолжительности переходного процесса.
Пороговое устройство, которое сравнивает выходной сигнал с заданным при настройке и который формирует команду на последующую разбраковку изделий, включается через некоторое время  после начала измерений. Динамическая погрешность при этом составляет:
после начала измерений. Динамическая погрешность при этом составляет:

где  и
и 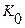 - передаточная функция и чувствительность измерительной системы,
- передаточная функция и чувствительность измерительной системы,
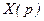 - преобразование Лапласа для входного сигнала.
- преобразование Лапласа для входного сигнала.
Но  , поэтому
, поэтому  и
и

Если динамика измерительной системы описывается дифференциальным уравнением первого порядка, то передаточная функция 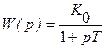 , где
, где  - постоянная времени системы, то
- постоянная времени системы, то
 .
.
Если  , то динамическая погрешность практически исчезает, но сам контрольный автомат теряет при этом свою производительность.
, то динамическая погрешность практически исчезает, но сам контрольный автомат теряет при этом свою производительность.
Определим вероятностные характеристики динамической погрешности. Случайными параметрами 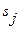 здесь являются:
здесь являются:
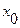 - случайная величина со средним значением
- случайная величина со средним значением  и дисперсией
и дисперсией 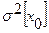 ;
;
 - случайная величина, рассеивание которой определяется погрешностями устройств, формирующих момент срабатывания пороговых схем, и имеющая математическое ожидание
- случайная величина, рассеивание которой определяется погрешностями устройств, формирующих момент срабатывания пороговых схем, и имеющая математическое ожидание  и дисперсию
и дисперсию 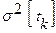 . Тогда динамическая погрешность будет характеризоваться математическим ожиданием
. Тогда динамическая погрешность будет характеризоваться математическим ожиданием

дисперсией

Так, если;
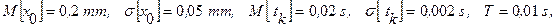
то:

Математическое ожидание – это систематическая погрешность и ее воздействие можно устранить соответствующей настройкой измерительной системы с учетом ее динамических свойств. Но случайная составляющая динамической погрешности полностью входит в суммарную погрешность средства измерений.
2. Измеряется овальность действительно овальной детали при непрерывном ее вращении
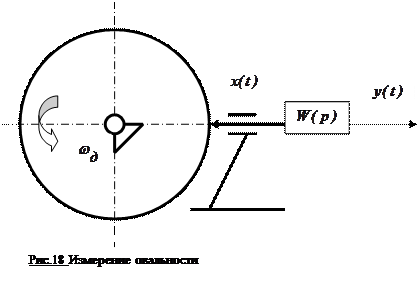 (рис. 18) на позиции измерения. Измерительная система обладает передаточной функцией колебательного звена:
(рис. 18) на позиции измерения. Измерительная система обладает передаточной функцией колебательного звена:
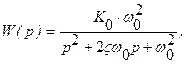
где 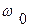 - частота собственных свободных колебаний измерительной системы,
- частота собственных свободных колебаний измерительной системы, 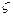 - степень успокоения колебаний.
- степень успокоения колебаний.
Входной сигнал имеет вид:

где: 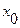 - постоянная составляющая, определяемая настройкой преобразователя,
- постоянная составляющая, определяемая настройкой преобразователя,
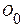 - овальность изделия (измеряемая случайная величина),
- овальность изделия (измеряемая случайная величина),
 - частота вращения изделия на позиции измерения,
- частота вращения изделия на позиции измерения,
 - случайная начальная фаза.
- случайная начальная фаза.
Таким образом, сигнал является квазидетерминированным, со случайными параметрами 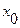 ,
, 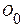 ,
,  и
и  . Динамическая погрешность измерения составляет:
. Динамическая погрешность измерения составляет:

Уже на этом шаге решение получается очень сложным. Однако здесь можно воспользоваться тем обстоятельством, что входной сигнал является синусоидальным, поэтому в установившемся режиме и выходная величина меняется синусоидально:

где  и
и  - значения АЧХ и ФЧХ при
- значения АЧХ и ФЧХ при  . Нас интересует динамическая погрешность измерения только овальности, которая по результатам измерения составляет:
. Нас интересует динамическая погрешность измерения только овальности, которая по результатам измерения составляет:
 .
.
Поэтому погрешность измерения составляет:

поскольку

Таким образом, динамическая погрешность является мультипликативной и составляет:

Погрешность является систематической и при любом значении скорости вращения изделия на
 позиции измерения
позиции измерения  погрешность можно вычислить и исключить из результатов измерений. График зависимости погрешности измерения от
погрешность можно вычислить и исключить из результатов измерений. График зависимости погрешности измерения от  представлена на рис. 19.
представлена на рис. 19.
Однако, если скорость вращения изделия нестабильна и при среднем значении  обладает дисперсией
обладает дисперсией 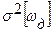 , то динамическая погрешность становится случайной с вероятностными характеристиками:
, то динамическая погрешность становится случайной с вероятностными характеристиками:
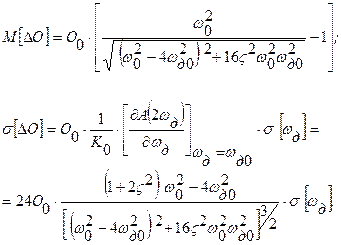
3). Задан энергетический спектр входного сигнала

и передаточная функция измерительной системы
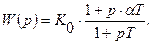
Требуется вычислить дисперсию собственной динамической погрешности.
Передаточная функция ошибки
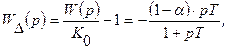
где  - некоторый безразмерный коэффициент, меньший единицы.
- некоторый безразмерный коэффициент, меньший единицы.
Энергетический спектр погрешности
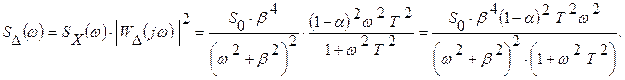
Дисперсия динамической погрешности составляет

Чтобы не мучиться с интегрированием, можно воспользоваться следующим обстоятельством.
Рассмотрим интегралы вида:
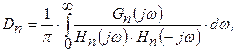
где

Результаты интегрирования этого выражения при некоторых  выглядят следующим образом:
выглядят следующим образом:

В нашем примере энергетический спектр погрешности можно представить в виде:
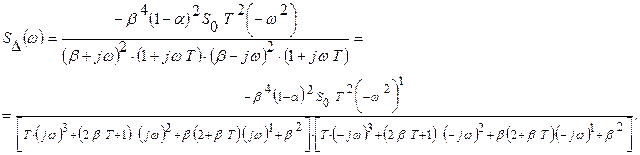
Сравнивая полученное выражение с тем, которым мы определили величину  , приходим к следующим выводам:
, приходим к следующим выводам:

Поэтому

Дата добавления: 2015-11-28; просмотров: 994;
