Определение погрешностей
Классы точности
Учёт всех метрологических характеристик средств измерения – очень сложная задача, поэтому для средств измерения, используемых в повседневной практике, принято деление их на классы точности.
Классом точности называется обобщённая характеристика всех средств измерения данного типа, обеспечивающая правильность их показания и устанавливающая оценку снизу точности показания.
В стандартах на средства измерения конкретного типа установлены требования к метрологическим характеристикам, в совокупности определяющих класс точности.
При маломеняющихся метрологических характеристиках допускается устанавливать требования, единые для 2 и более классов точности. Классы точности присваиваются типам средств измерения, с учётом результатов государственных приёмочных испытаний.
Средствам измерения с несколькими диапазонами изменения одной и той же физической величины или предназначенные для измерения разных физических величин, могут быть присвоены различные классы точности для каждого диапазона или каждой измеряемой величиной. Обозначения классов точности наносятся на циферблаты, щитки и корпуса средств измерения, приводятся в нормативно-технической документации. При этом рядом с обозначением стоит номер госта или технических условий, по которым он назначен.
Обозначения могут иметь форму заглавных букв латинского алфавита или римских цифр с добавлением условных знаков. Смысл таких обозначений указывается в нормативно-технической документации. Если класс точности обозначается арабскими цифрами с добавлением какого-либо условного знака, то эти цифры непосредственно устанавливают оценку снизу точности измерения.
Для средств измерения с равномерной и степенной шкалой, нулевое значение которой находится в середине ил на краю диапазона. Обозначение классов точности берётся из ряда (1; 1,5; 1,6; 2; 2,5; 3,4; 5,6). Это значит, что величина не отличается от того, что показывает указатель отсчётного устройства больше, чем на соответствующее число процентов от верхнего предела измерения.


 (0,5х200/100)=1
(0,5х200/100)=1
 120
120
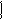
20 200
В
0,5 ГОСТ 874-85 (123£124£125)В
 |
Если 0 находится посередине шкалы, то для определения погрешности процент берётся от большего предела измерения.
Если средство измерения имеет номинальное значение, то процент берётся от номинального значения.
Если класс точности обведён в 0, то процент берётся от того числа, которое показывает указатель.
Определение погрешностей
Как отмечалось ранее, любое измерение по шкале отношений, предполагает сравнение неизвестного размера с известным и выражение первого через второе в кратном или дольном отношении. Q/[Q]
Это сравнение происходит под влиянием множества случайных и неслучайных факторов, точный учет которых невозможен, а результат совместного действия непредсказуем, т.е. уравнение измерений по шкале отношений имеет вид:
X= Q/[Q]+h (1),
где η носит случайный характер.
Если при измерениях используется тара, то X=(Q + V)/Q+ h (2),
где V – вес тары.
Из-за случайного характера η отсчет по шкале отношений получается все время разный. Это фундаментальное положение является законом природы. На основании громадного опыта практических измерений может быть сформулировано утверждение, называемое основным постулатом метрологии: отсчет является случайным числом. На этом основана вся метрология. Уравнение (2) является математической моделью измерения по шкале отношений. Отсчет не может быть представлен отдельным числом, его можно описать словами, математическими символами, представить массивом экспериментальных данных, таблицей, графиком, формулой и т.д. При ста измерениях одной и той же величины постоянного размера на цифровом табло измеряемого прибора случайным образом появляются значения xi, представленные в первой графе. Ни одно из чисел в первой графе таблицы, взятое в отдельности, не является отсчетом.
| xi | mi | P(xi) | F(xi) |
| 90,10 90,11 90,12 90,13 90,14 90,15 90,16 90,17 90,18 90,19 90,20 | . . . . . . | 0,01 0,02 0,05 0,1 . . . . . . 0,01 | 0,01 0,03 0,08 0,18 . . . . . . |
Отсчет характеризуется всей совокупностью чисел с учетом того, как часто они появляются. Принимая частость каждого i-го числа за вероятность его появления P(xi), заполним 3-ю графу. В совокупности с 1-ым столбцом, это даст нам распределение вероятности отсчета, представленное в виде таблицы. Графически это выглядит так.
P(xi) 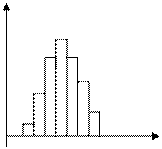
n
Представим в 4-ой графе вероятность того, что на табло измерительного прибора появится число, меньшее или равное тому, которое значится в 1-ой графе. В совокупности с 1-ой графой это даст нам представленную табличную функцию распределения вероятности отсчета.
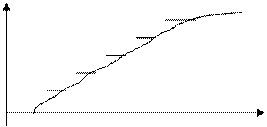 F(Xi)
F(Xi)
Хi
90,1 90,2
Как P(xi), так и F(xi) является исчерпывающим описанием отсчета у измерительных приборов. Описаниями отсчета могут быть также гистограмма и полигон.
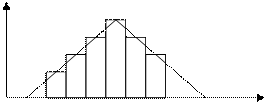 P(Xi)
P(Xi)
Xi
P(xi) и F(xi) служат в теории вероятностей моделями эмпирических законов распределения, полученных из экспериментальных данных методами математической статистики. После проведения процедуры измерения в уравнении (2) остаются неизвестными Q и η. Неслучайная V либо должна быть известна до измерения, либо установится в процессе дополнительных исследований. Слагаемое η является случайным и не может быть известно в принципе, поэтому определить значение измеряемой величины невозможно.
Q = x[Q] – η[Q] – V (3).
Равенство (3) соблюдается точно благодаря тому, что при повторных выполнениях измерительной процедуры случайное изменение 2-го слагаемого в правой части влечет за собой точно такой же изменение 1-го. О таких слагаемых говорят, что они коррелированны.
Разность между коррелированными значениями случайных величин не случайна, но в данном случае не известна. Поэтому строгого решения уравнение (3) не имеет. На практике пользуются приближенным решением, для этого используют результат специального исследования, называемого метрологической аттестацией средств измерений. В ходе этого исследования определяется среднее значение H ≈ η[Q]. Оно не является случайным, поэтому после замены случайного 2-го слагаемого в правой части получится
Q = x[Q] – H – V
В этом выражении результат измерения является случайным значением измеряемой величины
Q = x[Q] – H – V, где x[Q] – показание, [H – V] – поправка
x[Q] = X, Θ = - H – V
В результате получается Qi = xi + Qi. Результат измерения Q подчиняется тому же закону распределения вероятностей, что и показание, но смещенному по оси абсцисс на значение поправки. Следовательно, Qi – результат однократного измерения.
Результат многократного измерения запишется:
n
Qn=1/n S Qi
I=1
Математическая модель измерения по шкале порядка
Q1 + η1>< Q2 + η2
Результат измерения 2-х размеров по шкале порядка является случайным.
Дата добавления: 2015-12-11; просмотров: 636;
