Ситуационное моделирование
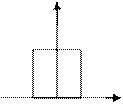
Решение уравнения 2 является приближенным из-за неточного знания поправки. Ситуации, по которой по какой-либо причине не хватает информации, часто встречаются в метрологии. Для математического описания используют Ситуационные модели. Предположим, что неизвестное значение Q, некоторое физ. величина. Требуется представить эту ситуацию в ситуационной модели. Если какие-либо значения Q более вероятны чем др., то это следует учесть. Если Q равновероятно на рассматриваемом интервале, то это можно описать следующей моделью:
 P(Q)
P(Q)
Q
-Qm Qm
Это графическое представление ситуации в которой значение Q, которое с одинаковой вероятностью, может быть любым на [-Qm; Qm].
2Qm*P(Q)=1. Отсюда можно записать функцию P(Q)=1/(2Qm)
Частные характеристики:
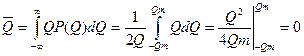

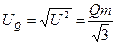
Пример:
Производят измерение. Измерением является метрическая линейка из тугоплавкого сплава. Чему ровна температурная поправка при измерении длины при 1000K?
Решение:
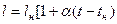 , где tн и lн – длина и температура соответствующая нормальным условия;
, где tн и lн – длина и температура соответствующая нормальным условия; 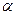 - коэффициент линейного температурного расширения.
- коэффициент линейного температурного расширения.
t - tн=1000k. Результат неизвестное значение l при t - tн=1000 в (1+1000 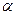 ) раз меньше L c lн
) раз меньше L c lн 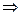 поправочный множитель À=1+1000
поправочный множитель À=1+1000 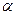 .
.
Поправка может быть аддитивной, мультипликативной. Аддитивная поправка возрастает: 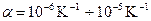
Значение сим. 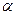 можно учесть с помощью ситуационной модели, согласно которой
можно учесть с помощью ситуационной модели, согласно которой 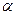 может быть от 10-5 до 10-6.
может быть от 10-5 до 10-6.
À=1+1000*10-5 ; À=1,0055
1+0,01
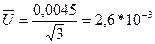
Дата добавления: 2015-12-11; просмотров: 602;
