Предел функции в точке
Предел функции. Производная
Понятие функции
Пусть задано множество 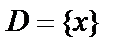 изменения переменной величины x. Если каждому значению величины
изменения переменной величины x. Если каждому значению величины 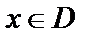 соответствует одно определённое значение величины y, то говорят, что на множестве D задана функция
соответствует одно определённое значение величины y, то говорят, что на множестве D задана функция 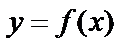 , т.е. величина y есть функция величины x.
, т.е. величина y есть функция величины x.
Величина x называется аргументом функции у, множество D – областью определения функции. Так как значение величины 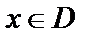 можно брать произвольно, а значение величины у зависит от выбранного значения х, то х называется независимой переменной, а у – зависимой переменной. Множество значений, принимаемых функцией у, называется областью значений функции.
можно брать произвольно, а значение величины у зависит от выбранного значения х, то х называется независимой переменной, а у – зависимой переменной. Множество значений, принимаемых функцией у, называется областью значений функции.
Графиком функции называется множество всех точек плоскости, абсциссы которых являются значениями независимой переменной, а ординаты – соответствующими значениями функции.
Значение функции при 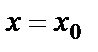 называется частным значением функции в точке
называется частным значением функции в точке  и обозначается
и обозначается 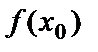 .
.
Пример 1. Вычислить значение функции  при
при 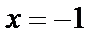 .
.
Решение. Частное значение данной функции в точке 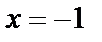 равно
равно 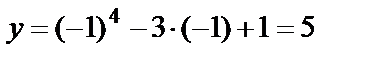 .
.
Пример 2. Найти область определения функции 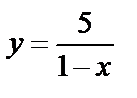 .
.
Решение. Так как 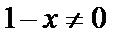 , т.е.
, т.е. 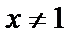 , то
, то  .
.
Пример 3. Найти область определения функции 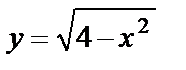 .
.
Решение. Выражение под знаком корня квадратного должно быть неотрицательным, т.е. 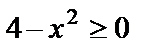 . Решим это неравенство методом интервалов:
. Решим это неравенство методом интервалов: 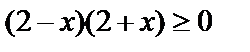 ,
,
| ● -2 |
| ● |
| х |
| − |
| − |
| + |
Таким образом, 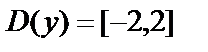 .
.
Пример 4. Найти область определения функции  .
.
Решение. Для данной функции 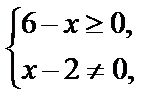 т.е.
т.е. 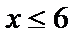 и
и  . Поэтому
. Поэтому 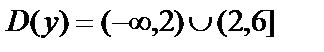 .
.
Пусть функция  определена на множестве
определена на множестве 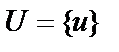 , а функция
, а функция 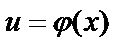 – на множестве
– на множестве 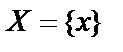 , причём все значения функции
, причём все значения функции 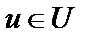 . Тогда переменная у является функцией от х:
. Тогда переменная у является функцией от х: 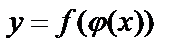 . В этом случае у называется сложной функцией, а переменная u – промежуточным аргументом. Например,
. В этом случае у называется сложной функцией, а переменная u – промежуточным аргументом. Например, 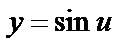 и
и 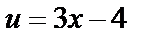 . Тогда
. Тогда 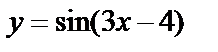 является сложной функцией.
является сложной функцией.
Предел функции в точке
Число А называется пределом функции 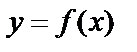 при
при 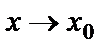 , если для всех значений х, достаточно близких к
, если для всех значений х, достаточно близких к 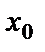 , соответствующие значения функции как угодно мало отличаются от числа А. Записывается это следующим образом:
, соответствующие значения функции как угодно мало отличаются от числа А. Записывается это следующим образом:
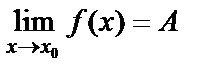 или
или 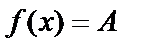 при
при 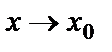 .
.
В определении предела  может быть любым конечным числом или же обозначать
может быть любым конечным числом или же обозначать 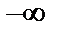 и
и 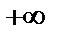 .
.
При вычислении пределов пользуются следующими правилами:
1) предел постоянной величины равен самой величине, т.е.
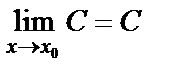 ;
;
2) предел алгебраической суммы конечного числа функций равен алгебраической сумме пределов этих функций при условии, что пределы существуют, т.е. для двух функций справедливо равенство
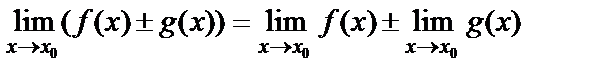 ;
;
3) предел произведения конечного числа функций равен произведению их пределов при условии, что эти пределы существуют, т.е. для двух функций справедливо равенство
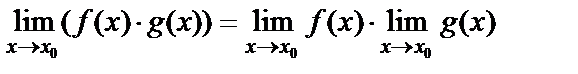 ;
;
4) если n – натуральное число, то
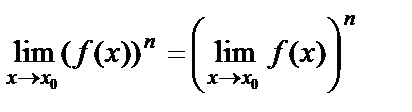 ;
;
5) постоянный множитель можно выносить за знак предела, т.е.
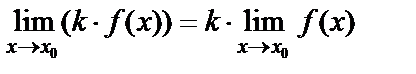 ;
;
6) предел отношения двух функций равен отношению их пределов, если последние существуют и предел знаменателя отличен от нуля, т.е.
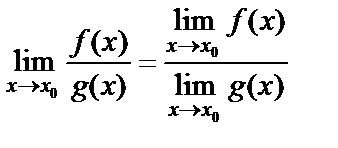 , если
, если  .
.
При вычислении пределов функции иногда приходится пользоваться понятием односторонних пределов. Пусть функция 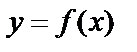 определена на множестве
определена на множестве 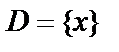 и пусть
и пусть 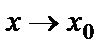 . Будем рассматривать такие значения х, что
. Будем рассматривать такие значения х, что 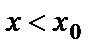 . Это означает, что
. Это означает, что 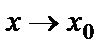 , оставаясь всё время слева от
, оставаясь всё время слева от 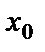 . Если при этом существует предел функции
. Если при этом существует предел функции 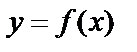 при
при 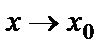 , то он называется левым пределом этой функции в точке
, то он называется левым пределом этой функции в точке 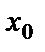 или при
или при 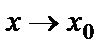 и обозначается
и обозначается 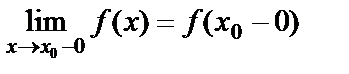 .
.
Пусть теперь 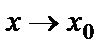 , оставаясь всё время справа от
, оставаясь всё время справа от 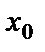 , т.е. оставаясь больше
, т.е. оставаясь больше 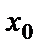 . Если при этом существует предел функции
. Если при этом существует предел функции 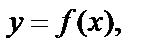 то он называется правым пределом этой функции в точке
то он называется правым пределом этой функции в точке 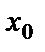 или при
или при 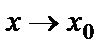 и обозначается
и обозначается 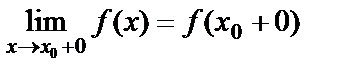 .
.
Левый и правый пределы называются односторонними пределами функции в точке. Если односторонние пределы функции 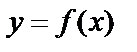 в точке
в точке 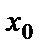 существуют и равны между собой, то функция имеет тот же предел в этой точке:
существуют и равны между собой, то функция имеет тот же предел в этой точке: 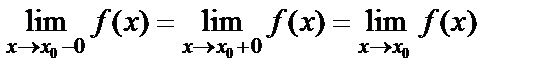 .
.
Если односторонние пределы функции в точке 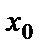 существуют, но не равны между собой, то предел функции в этой точке не существует.
существуют, но не равны между собой, то предел функции в этой точке не существует.
Пример 5. Найти предел функции 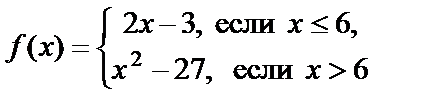 в точке x=6.
в точке x=6.
Решение. Найдём односторонние пределы функции в данной точке. Если 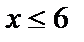 , то
, то 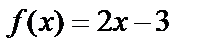 и
и 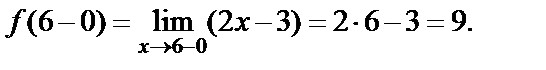 Если x>6, то
Если x>6, то 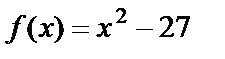 и
и 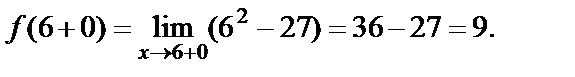 Так как односторонние пределы в точке x=6 равны между собой, то предел функции в этой точке существует и равен 9.
Так как односторонние пределы в точке x=6 равны между собой, то предел функции в этой точке существует и равен 9.
Дата добавления: 2015-12-10; просмотров: 1083;
