Производные высших порядков

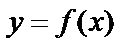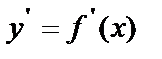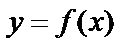Пусть функция в области D имеет конечную производную , которая в свою очередь также является функцией от переменной х в этой же области. Производная называется производной первого порядка. Если существует производная от производной первого порядка, то она называется производной второго порядка или второй производной от функции и обозначается или 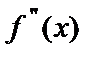. Производная от производной второго порядка называется производной третьего порядка или третьей производной и обозначается 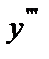или 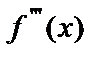и т.д. Производные, начиная со второго порядка и выше, называются производными высших порядков.

Пример 13. Найти производную четвёртого порядка функции .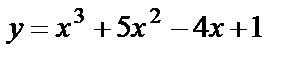

Решение. ; ; ; .

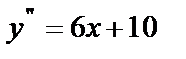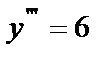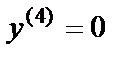Экстремум функции

При исследовании функции приходится определять характер её поведения. Для этого можно использовать средства дифференциального исчисления.

Пусть функция дифференцируема в интервале (a,b). Тогда справедливы следующие утверждения:

1) если производная 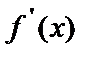в интервале (a,b) положительна, то функция в этом интервале возрастает;

2) если производная 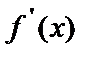в интервале (a,b) отрицательна, то функция в этом интервале убывает.

Эти утверждения являются достаточными условиями возрастания и убывания (монотонности) функции.

Пример 14. Исследовать функцию 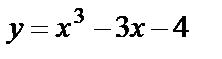на монотонность.

Решение. Функция определена на всём множестве действительных чисел, т.е. . Найдём производную: 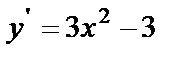. Функция возрастает, если , т.е. 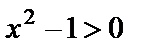или же 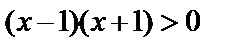. Решив это неравенство, получим, что функция возрастает при 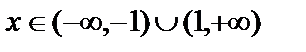. Функция убывает, если 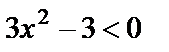, т.е. 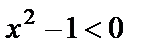или 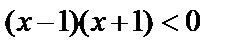. Решив последнее неравенство, получим, что при функция убывает. Таким образом, интервалами монотонности функции являются .

Особую роль в исследовании функции играют такие значения х, которые отделяют интервалы возрастания и убывания функции. В этих точках функция меняет характер своего поведения.

Функция 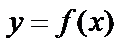имеет в точке максимум, если есть наибольшее значение этой функции в некоторой окрестности данной точки. Функция 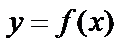имеет в точке минимум, если есть наименьшее значение этой функции в некоторой окрестности данной точки.

Точки максимума и минимума называются точками экстремума, а максимум и минимум называются экстремумами функции.

Если в точке 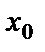функция 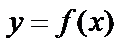достигает экстремума, то её производная в этой точке либо равна нулю, либо не существует. Это утверждение является необходимым признаком (условием) экстремума.

Следует иметь в виду, что необходимый признак экстремума не является достаточным. Это означает, что если в какой-то точке производная функции равна нулю, то эта точка не обязательно будет точкой экстремума.

Точки, в которых производная функции равна нулю либо не существует, называются критическими (стационарными).

Пусть функция 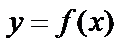непрерывна в некоторой окрестности точки 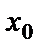и всюду в этой окрестности имеет производную, а в точке 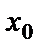производная либо равна нулю, либо не существует. Тогда имеет место первый достаточный признак (первое достаточное условие) экстремума:

1) если при переходе через точку 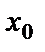слева направо производная функции меняет знак с «+» на «-», то в точке функция имеет максимум;

2) если при переходе через точку 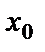слева направо производная функции меняет знак с «-» на «+», то в точке 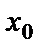функция имеет минимум;

3) если при переходе через точку 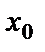производная функции не меняет знак, то в точке 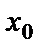функция экстремума не имеет.

При исследовании функции на экстремум имеет смысл придерживаться следующей схемы:

1) найти область определения функции;

2) найти производную функции и приравнять её нулю;

3) решить полученное уравнение 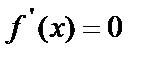и найти критические точки;

4) в области определения функции найти те точки, в которых производная 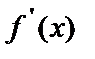либо равна нулю, либо не существует;

5) все полученные точки расположить в порядке возрастания и разбить область определения этими точками на частичные интервалы, в каждом из которых производная сохраняет знак. Таким образом, частичные интервалы являются интервалами монотонности функции;

6) найти знак производной в каждом из частичных интервалов и по знаку производной определить характер изменения функции в каждом из этих интервалов: возрастает или убывает;

7) по изменению знака производной при переходе через границы интервалов монотонности определить точки экстремума;

8) вычислить значения функции в точках экстремума.

Пример 15. Найти экстремум функции .

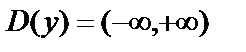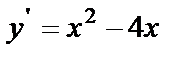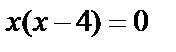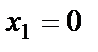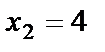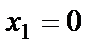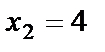Решение. Функция определена на всей числовой прямой, т.е. . Найдём производную, приравняем её нулю и решим полученное уравнение: , , , , . Точки и являются критическими. Разобьём область определения функции критическими точками на частичные интервалы, которые являются интервалами монотонности функции, и по знаку производной определим характер изменения функции в каждом из этих интервалов:

x		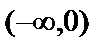	(0,4)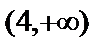
y	возрастает	max	убывает	-9 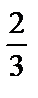min	возрастает
	+		_		+

; ;

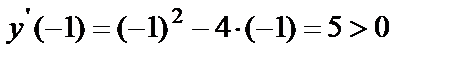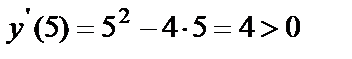. По первому достаточному признаку экстремума в точке х=0 функция имеет максимум, а в точке х=4 – минимум. При этом: 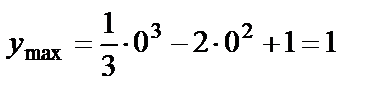, 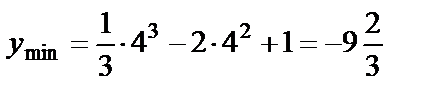. Таким образом, у=1 и 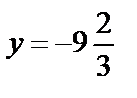являются экстремумами функции.