Расчет простых электрических цепей постоянного тока
Рассмотрим электрическую цепь, изображенную на рис. 1. Пусть известны величины сопротивлений резисторов 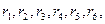 э. д. с. E и ее внутреннее сопротивление
э. д. с. E и ее внутреннее сопротивление 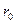 . Требуется определить токи во всех участках цепи и напряжение, которое покажет вольтметр (сопротивление его бесконечно велико), включенный между точками схемы
. Требуется определить токи во всех участках цепи и напряжение, которое покажет вольтметр (сопротивление его бесконечно велико), включенный между точками схемы 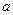 и
и 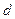 .
.
Такие задачи решаются методом свертывания схемы, по которому отдельные участки схемы упрощают и постепенным преобразованием приводят схему к одному эквивалентному (входному) сопротивлению относительно зажимов источника питания. Схема упрощается с помощью замены группы последовательно или параллельно соединенных сопротивлений одним эквивалентным сопротивлением. Так, сопротивления 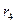 и
и 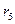 соединены последовательно и их эквивалентное сопротивление
соединены последовательно и их эквивалентное сопротивление
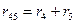
Сопротивления 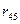 и
и 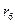 соединены параллельно и, следовательно, их эквивалентное сопротивление
соединены параллельно и, следовательно, их эквивалентное сопротивление
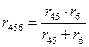
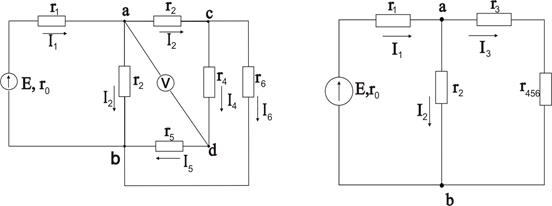
Рис. 1 Рис. 2
После произведенных преобразований цепь принимает вид, показанный на рис. 2, а эквивалентное сопротивление всей цепи найдем из уравнения
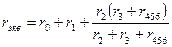
Ток 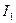 в неразветвленной части схемы определим по закону Ома:
в неразветвленной части схемы определим по закону Ома:
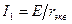
Воспользовавшись схемой на рис. 2, найдем токи 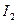 и
и 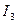 :
:
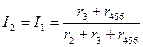 ;
; 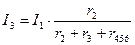 .
.
Переходя к рис. 1,определим токи 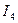 ;
; 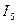 и
и 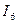 по аналогичным уравнениям:
по аналогичным уравнениям:
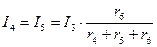 ;
; 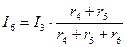
Зная ток 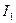 можно найти ток
можно найти ток 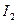 другим способом. Согласно второму закону Кирхгофа,
другим способом. Согласно второму закону Кирхгофа, 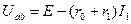 тогда
тогда
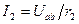
Показание вольтметра можно определить, составив уравнение по второму закону Кирхгофа, например, для контура 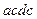 :
:
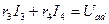 .
.
Для проверки решения можно воспользоваться первым законом Кирхгофа и уравнением баланса мощностей, которые для схемы, изображенной на рис. 1, примут вид
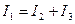 ;
; 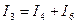
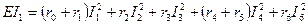
Простые электрические цепи можно рассчитывать методом подобия (метод пропорциональных величин), который применим только для расчета линейных цепей, т. е. цепей с неизменными величинами сопротивлений. Воспользуемся свойством линейных цепей для определения токов схемы, изображенной на рис. 1, в следующей последовательности. Задаемся произвольным значением тока 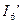 в сопротивлении
в сопротивлении 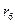 , наиболее удаленном от источника питания. По заданному
, наиболее удаленном от источника питания. По заданному 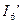 и сопротивлению определяем напряжение
и сопротивлению определяем напряжение 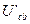 :
:
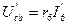
Далее определяем:
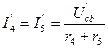 ;
; 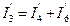 ;
; 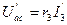 ;
; 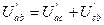
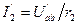 ;
; 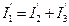
Наконец, находим величину э. д. с. 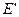 :
:
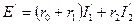
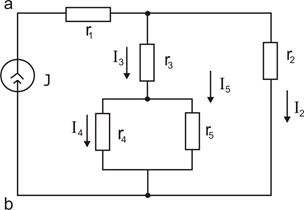
Рис. 3
Однако найденное значение э. д. с. 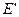 в общем случае отличается от заданной величины э. д. с.
в общем случае отличается от заданной величины э. д. с. 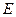 . Поэтому для определения действительных значений токов и напряжений вычисляем так называемый коэффициент подобия
. Поэтому для определения действительных значений токов и напряжений вычисляем так называемый коэффициент подобия 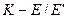 . Умножив на него полученные при расчете значения токов и напряжении, находим действительное значение токов схемы. Метод пропорциональных величин особенно эффективен при расчете разветвленных линейных электрических цепей с одним источником.
. Умножив на него полученные при расчете значения токов и напряжении, находим действительное значение токов схемы. Метод пропорциональных величин особенно эффективен при расчете разветвленных линейных электрических цепей с одним источником.
Рассмотрим электрическую цепь, изображенную на рис. 3. К источнику тока 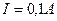 подключены резисторы с сопротивлениями
подключены резисторы с сопротивлениями 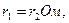
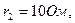
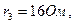
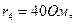
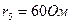 . Определить напряжение
. Определить напряжение 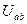 источника тока и все токи. Составить баланс мощностей. Задача решается методом свертывания схемы.
источника тока и все токи. Составить баланс мощностей. Задача решается методом свертывания схемы.
Находим входное сопротивление 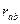 схемы относительно зажимов источника тока:
схемы относительно зажимов источника тока:
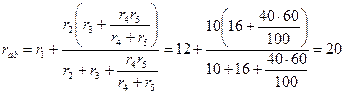 Ом
Ом
Находим напряжение на зажимал источника тока 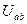 :
:
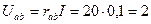 В
В
По закону Ома находим ток 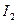 :
:
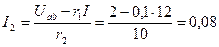 А
А
Ток 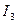 определяем из уравнения первого закона Кирхгофа:
определяем из уравнения первого закона Кирхгофа:
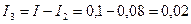 А
А
Этот ток распределяется обратно пропорционально сопротивлениям 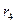 и
и 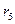 :
:
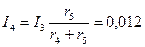 А;
А; 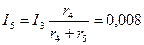 А.
А.
Уравнение баланса мощностей отражает равенство мощностей, отдаваемой источником и расходуемой приемниками, т. е.
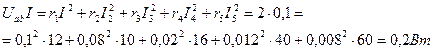
Следовательно,
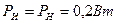
Дата добавления: 2015-12-10; просмотров: 1824;
